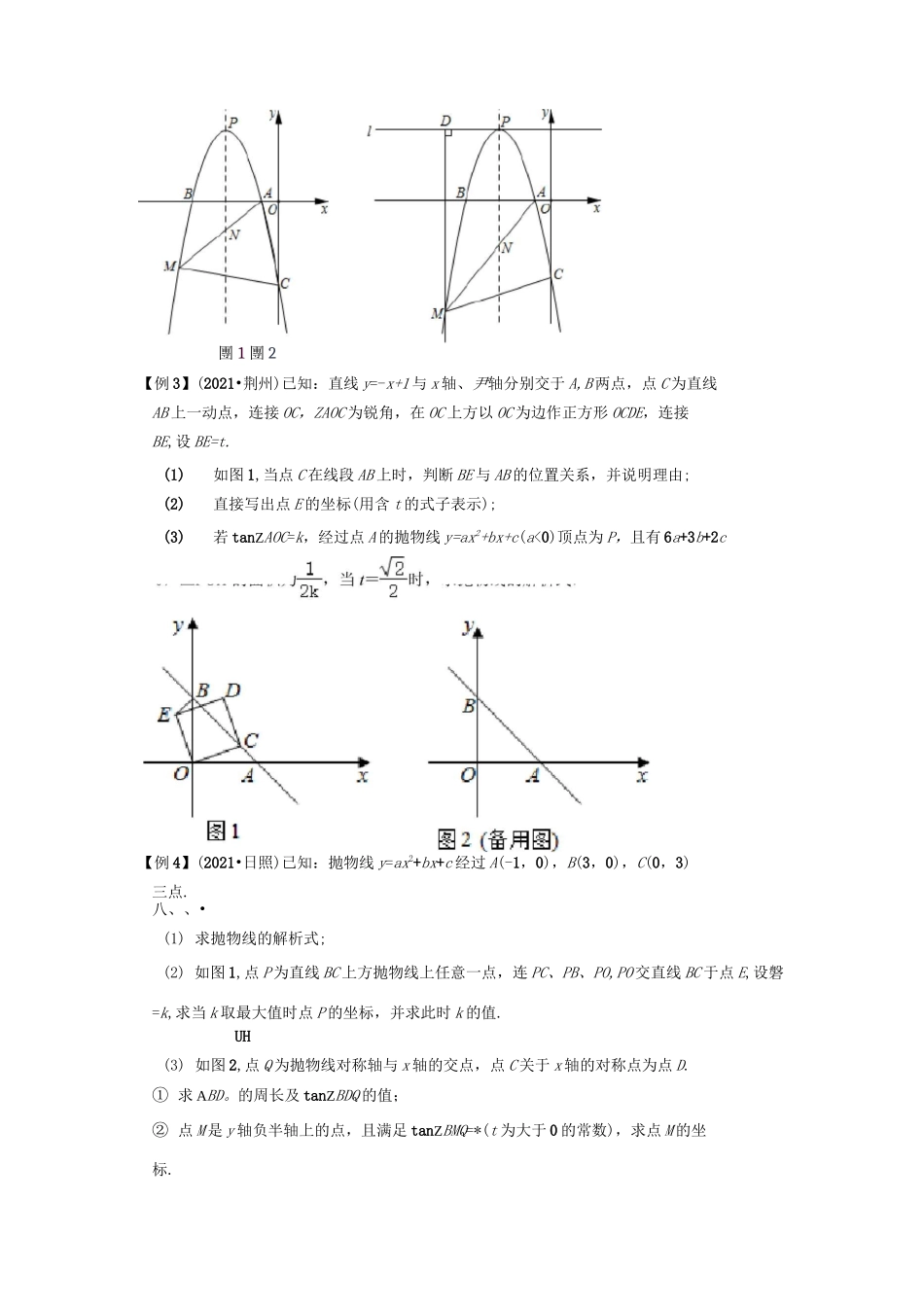
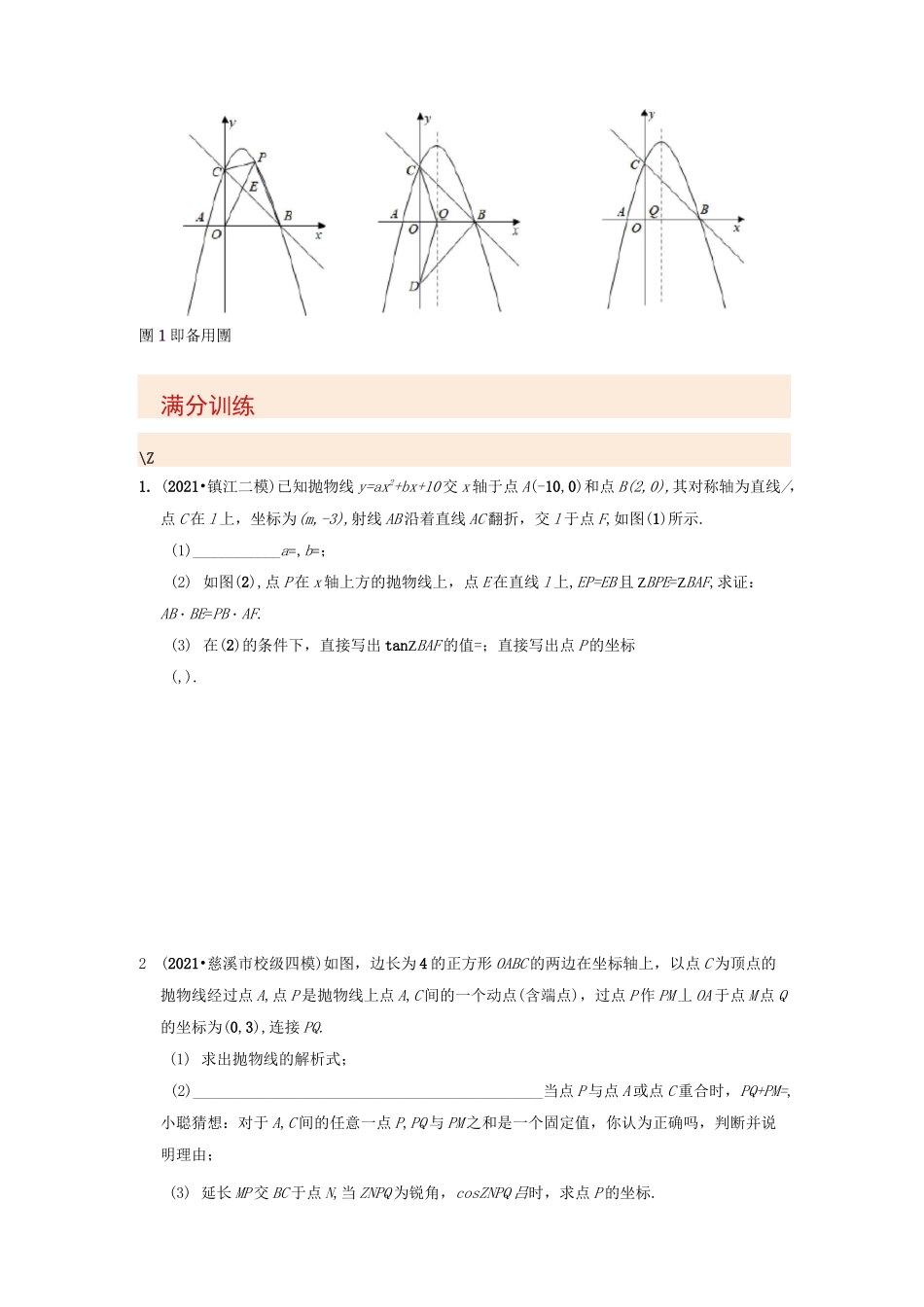
挑战2022年中考数学压轴题之学霸秘笈大揭秘专题17二次函数与三角函数综合问题典例剖析-【例1】(2021•盘锦)如图,抛物线尹=-壬好+2%+6与x轴交于A,B两点(点A在点B的左侧),与尹轴交于点C,直线尹=x-2与尹轴交于点D,与x轴交于点E,与直线BC交于点F.(1)______________________点F的坐标为;(2)如图1,点P为第一象限抛物线上的一点,PF的延长线交OB于点Q,PMLBC于点M,QN丄BC于点N,若黒_=丄土,求点P的坐标;~QN4(3)如图2,点S为第一象限抛物线上的一点,且点S在射线DE上方,动点G从点E出发,沿射线DE方向以每秒4卫个单位长度的速度运动,当SE=SG,且tanZSEG=*图1團2【例2】(2021・十堰)已知抛物线y=ax2+bx-5与x轴交于点A(-1,0)和B(-5,0),与y轴交于点C,顶点为P,点N在抛物线对称轴上且位于x轴下方,连AN交抛物线于M,连AC、CM.(1)求抛物线的解析式;(2)如图1,当tanZACM=2时,求M点的横坐标;(3)如图2,过点P作x轴的平行线1,过M作MD丄l于D,若MD=•~^MN,求N点的坐标.=0,△POA的面积为,求抛物线的解析式.團1團2【例3】(2021•荆州)已知:直线y=-x+1与x轴、尹轴分别交于A,B两点,点C为直线AB上一动点,连接OC,ZAOC为锐角,在OC上方以OC为边作正方形OCDE,连接BE,设BE=t.(1)如图1,当点C在线段AB上时,判断BE与AB的位置关系,并说明理由;(2)直接写出点E的坐标(用含t的式子表示);(3)若tanZAOC=k,经过点A的抛物线y=ax2+bx+c(a<0)顶点为P,且有6a+3b+2c【例4】(2021•日照)已知:抛物线y=ax2+bx+c经过A(-1,0),B(3,0),C(0,3)三点.八、、•(1)求抛物线的解析式;(2)如图1,点P为直线BC上方抛物线上任意一点,连PC、PB、PO,PO交直线BC于点E,设磐=k,求当k取最大值时点P的坐标,并求此时k的值.UH(3)如图2,点Q为抛物线对称轴与x轴的交点,点C关于x轴的对称点为点D.①求ABD。的周长及tanZBDQ的值;②点M是y轴负半轴上的点,且满足tanZBMQ=*(t为大于0的常数),求点M的坐标.團1即备用團满分训练\Z1.(2021•镇江二模)已知抛物线y=ax2+bx+10交x轴于点A(-10,0)和点B(2,0),其对称轴为直线/,点C在l上,坐标为(m,-3),射线AB沿着直线AC翻折,交l于点F,如图(1)所示.(1)____________a=,b=;(2)如图(2),点P在x轴上方的抛物线上,点E在直线l上,EP=EB且ZBPE=ZBAF,求证:AB・BE=PB・AF.(3)在(2)的条件下,直接写出tanZBAF的值=;直接写出点P的坐标(,).2(2021•慈溪市校级四模)如图,边长为4的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A,C间的一个动点(含端点),过点P作PM丄OA于点M点Q的坐标为(0,3),连接PQ.(1)求出抛物线的解析式;(2)______________________________________________当点P与点A或点C重合时,PQ+PM=,小聪猜想:对于A,C间的任意一点P,PQ与PM之和是一个固定值,你认为正确吗,判断并说明理由;(3)延长MP交BC于点N,当ZNPQ为锐角,cosZNPQ吕时,求点P的坐标.團⑴图⑵-2交尹轴于点力,该抛物线的顶点为B(2,-4).(1)如图(1),求a,b的值;(2)如图(2),过点B作x轴的垂线,点C为垂足,横坐标为t的点P在抛物线上,点P在第四象限且位于BC右侧,连接PA,PC,△ACP的面积为S,求S与t之间的函数关系式,不要求写出自变量t的取值范围;(3)如图(3),在(2)的条件下,连接PB,点D与点A关于原点对称,过点D作x轴的平行线与抛物线在第二象限交于点点F在第三象限,点G在CB的延长线上,若EF=PC,ZDEF+ZBCP=150°,ZDEG-ZPFG=30°,tanZEGF=^,求点P■34.(2021•金坛区模拟)如图,在平面直角坐标系xOy中,已知二次函数y=-专(x-2)2的图象与y轴交于点B,抛物线的对称轴是直线1,顶点是A,过点B作CD丄BA交x轴于点C,交抛物线于点D,连接AD.将线段AB沿线段AD平移得到EF(点E与点A对应、点F与点B对应),连接BF.(2)若点F恰好落在直线L上,求AF的长;(3)连接DF并延长交抛物线于点Q,若tanZADF=*,求点Q的坐标.5.(2021•仙桃校级模拟)如图,已知抛物线Ci:y=ax2+bx+c的顶点坐标为(0,-2),且经过点A(-2,2),动直线l的解析式为:y=-4x+e.(1)求抛物线C1的解析式;(2)将抛物线C1向上平移两个单位得到新抛物线C2,过点A的直线交抛物线C2于M、N两点(M位于点N的左边),动直线经过点M,与抛物线C2的另...