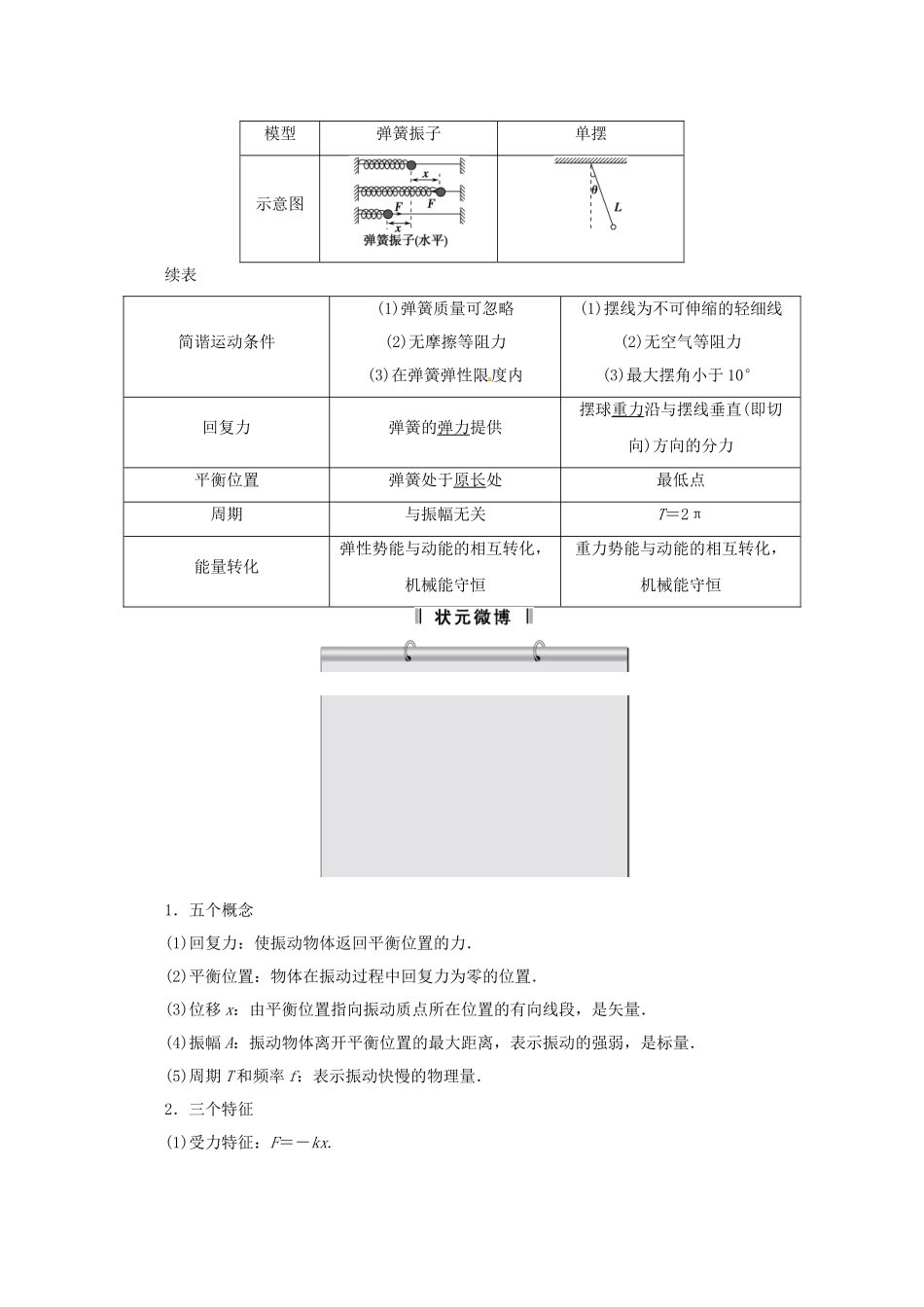
选修3-4机械振动机械波光电磁波相对论简介第1讲机械振动简谐运动Ⅰ(考纲要求)【思维驱动】(单选)如图1-1-1所示,弹簧振子在B、C间振动,O为平衡位置,BO=OC=5cm,若振子从B到C的运动时间是1s,则下列说法正确的是().图1-1-1A.振子从B经O到C完成一次全振动B.振动周期是1s,振幅是10cmC.经过两次全振动,振子通过的路程是20cmD.从B开始经过3s,振子通过的路程是30cm解析振子从B→O→C仅完成了半次全振动,所以周期T=2×1s=2s,振幅A=BO=5cm.弹簧振子在一次全振动过程中通过的路程为4A=20cm,所以两次全振动中通过路程为40cm,3s的时间为1.5T,所以振子通过的路程为30cm.答案D【知识存盘】1.简谐运动(1)定义:物体在跟位移大小成正比并且总是指向平衡位置的回复力作用下的振动.(2)简谐运动的特征①动力学特征:F回=-kx.②运动学特征:x、v、a均按正弦或余弦规律发生周期性变化(注意v、a的变化趋势相反).③能量特征:系统的机械能守恒,振幅A不变.2.简谐运动的两种模型模型弹簧振子单摆示意图续表简谐运动条件(1)弹簧质量可忽略(2)无摩擦等阻力(3)在弹簧弹性限度内(1)摆线为不可伸缩的轻细线(2)无空气等阻力(3)最大摆角小于10°回复力弹簧的弹力提供摆球重力沿与摆线垂直(即切向)方向的分力平衡位置弹簧处于原长处最低点周期与振幅无关T=2π能量转化弹性势能与动能的相互转化,机械能守恒重力势能与动能的相互转化,机械能守恒1.五个概念(1)回复力:使振动物体返回平衡位置的力.(2)平衡位置:物体在振动过程中回复力为零的位置.(3)位移x:由平衡位置指向振动质点所在位置的有向线段,是矢量.(4)振幅A:振动物体离开平衡位置的最大距离,表示振动的强弱,是标量.(5)周期T和频率f:表示振动快慢的物理量.2.三个特征(1)受力特征:F=-kx.(2)运动特征:a=-x.(3)能量特征:系统机械能守恒.简谐运动的表达式和图象Ⅰ(考纲要求)【思维驱动】如图1-1-2所示为一弹簧振子的振动图象,求:图1-1-2(1)该振子简谐运动的表达式.(2)在第2s末到第3s末这段时间内,弹簧振子的加速度、速度、动能和弹性势能各是怎样变化的?(3)该振子在前100s的总位移是多少?路程是多少?解析(1)由振动图象可得:A=5cm,T=4s,φ=0则ω==rad/s故该振子做简谐运动的表达式为:x=5sint(cm).(2)由题图可知,在t=2s时振子恰好通过平衡位置,此时加速度为零,随着时间的延续,位移值不断加大,加速度的值也变大,速度值不断变小,动能不断减小,弹性势能逐渐增大.当t=3s时,加速度的值达到最大,速度等于零,动能等于零,弹性势能达到最大值.(3)振子经过一个周期位移为零,路程为5×4cm=20cm,前100s刚好经过了25个周期,所以前100s振子位移x=0,振子路程s=20×25cm=500cm=5m.答案(1)x=5sintcm(2)见解析(3)05m【知识存盘】1.简谐运动的表达式(1)动力学表达式:F=-kx,“”其中-表示回复力与位移的方向相反.(2)运动学表达式:x=Asin(ωt+φ),其中A代表振幅,ω=2πf表示简谐运动的快慢,(ωt+φ)代表简谐运动的相位,φ叫做初相.2.简谐运动的图象(1)从平衡位置开始计时,函数表达式为x=Asinωt,图象如图1-1-3甲所示.图1-1-3(2)从最大位移处开始计时,函数表达式为x=Acosωt,图象如图乙所示.简谐运动的对称性(1)瞬时量的对称性(2)过程量的对称性:振动质点来回通过相同的两点间的时间相等,如tBC=tCB;质点经过关于平衡位置对称的等长的两线段时时间相等,如tBC=tB′C′,如图1-1-4所示.图1-1-4受迫振动和共振Ⅰ(考纲要求)【思维驱动】一砝码和一轻弹簧构成弹簧振子,如图1-1-5甲所示,该装置可用于研究弹簧振子的受迫振动.匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动.把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期.若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图乙所示.当把手以某一速度匀速运动,受迫振动达到稳定时,砝码的振动图象如图丙所示.若用T0表示弹簧振子的固有周期,T表示驱动力的周期,r表示受迫振动达到稳定后砝码振动的振幅,则...