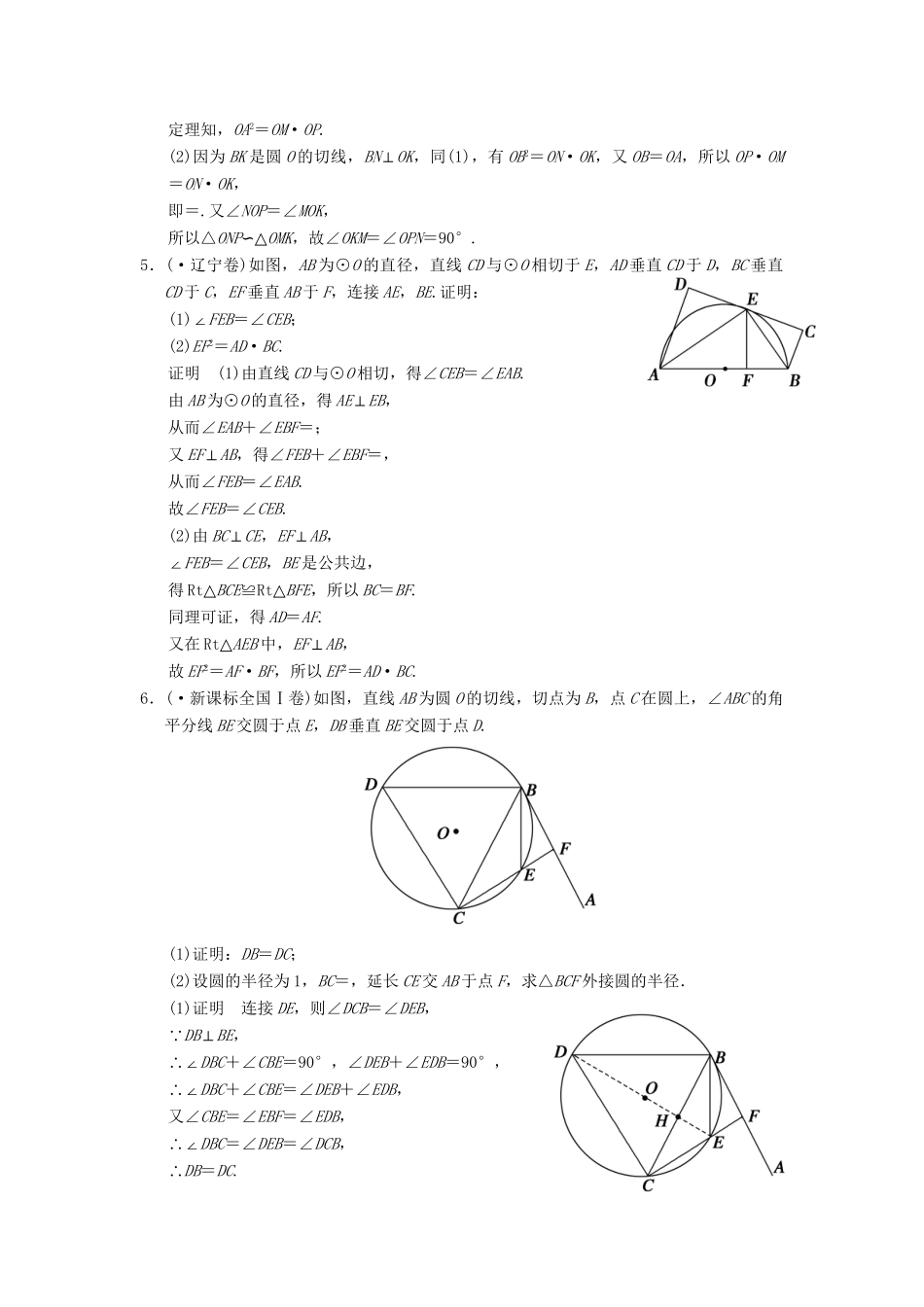
常考问题19几何证明选讲1.(·江苏卷)如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2),圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB∶AC为定值.证明如图,连接AO1并延长,分别交两圆于点E和点D.连接BD,CE.因为圆O1与圆O2内切于点A,所以点O2在AD上,故AD,AE分别为圆O1,圆O2的直径.从而∠ABD=∠ACE=.所以BD∥CE,于是===.所以AB∶AC为定值.2.(·苏北四市质量检测)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA.证明连接OT,因为AT是切线,所以OT⊥AP.又因为∠PAQ是直角,即AQ⊥AP,所以AB∥OT,所以∠TBA=∠BTO.又OT=OB,所以∠OTB=∠OBT,所以∠OBT=∠TBA,即BT平分∠OBA.3.(·江苏卷)AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC.证明连接OD,则:OD⊥DC,又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,∠DOC=∠DAO+∠ODA=2∠DCO,所以∠DCO=30°,∠DOC=60°,所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC.4.如图,过圆O外一点M作它的一条切线,切点为A,过A点作直线AP垂直直线OM,垂足为P.(1)证明:OM·OP=OA2;(2)N为线段AP上一点,直线NB垂直直线ON,且交圆O于B点.过B点的切线交直线ON于K.证明:∠OKM=90°.证明(1)因为MA是圆O的切线,所以OA⊥AM.又因为AP⊥OM,在Rt△OAM中,由射影定理知,OA2=OM·OP.(2)因为BK是圆O的切线,BN⊥OK,同(1),有OB2=ON·OK,又OB=OA,所以OP·OM=ON·OK,即=.又∠NOP=∠MOK,所以△ONP∽△OMK,故∠OKM=∠OPN=90°.5.(·辽宁卷)如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明:(1)∠FEB=∠CEB;(2)EF2=AD·BC.证明(1)由直线CD与⊙O相切,得∠CEB=∠EAB.由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=;又EF⊥AB,得∠FEB+∠EBF=,从而∠FEB=∠EAB.故∠FEB=∠CEB.(2)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,得Rt△BCE≌Rt△BFE,所以BC=BF.同理可证,得AD=AF.又在Rt△AEB中,EF⊥AB,故EF2=AF·BF,所以EF2=AD·BC.6.(·新课标全国Ⅰ卷)如图,直线AB为圆O的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.(1)证明:DB=DC;(2)设圆的半径为1,BC=,延长CE交AB于点F,求△BCF外接圆的半径.(1)证明连接DE,则∠DCB=∠DEB,∵DB⊥BE,∴∠DBC+∠CBE=90°,∠DEB+∠EDB=90°,∴∠DBC+∠CBE=∠DEB+∠EDB,又∠CBE=∠EBF=∠EDB,∴∠DBC=∠DEB=∠DCB,∴DB=DC.(2)解由(1)知:∠CBE=∠EBF=∠BCE,∴∠BDE=∠CDE,∴DE是BC的垂直平分线,设交点为H,则BH=,∴OH==,∴DH=,∴tan∠BDE==,∴∠BDE=30°,∴∠FBE=∠BDE=30°,∴∠CBF+∠BCF=90°,∴∠BFC=90°,∴BC是△BCF的外接圆直径.∴△BCF的外接圆半径为.备课札记: