北京体育大学附中版高考数学一轮复习 空间几何体单元突破训练 新人教A版VIP免费

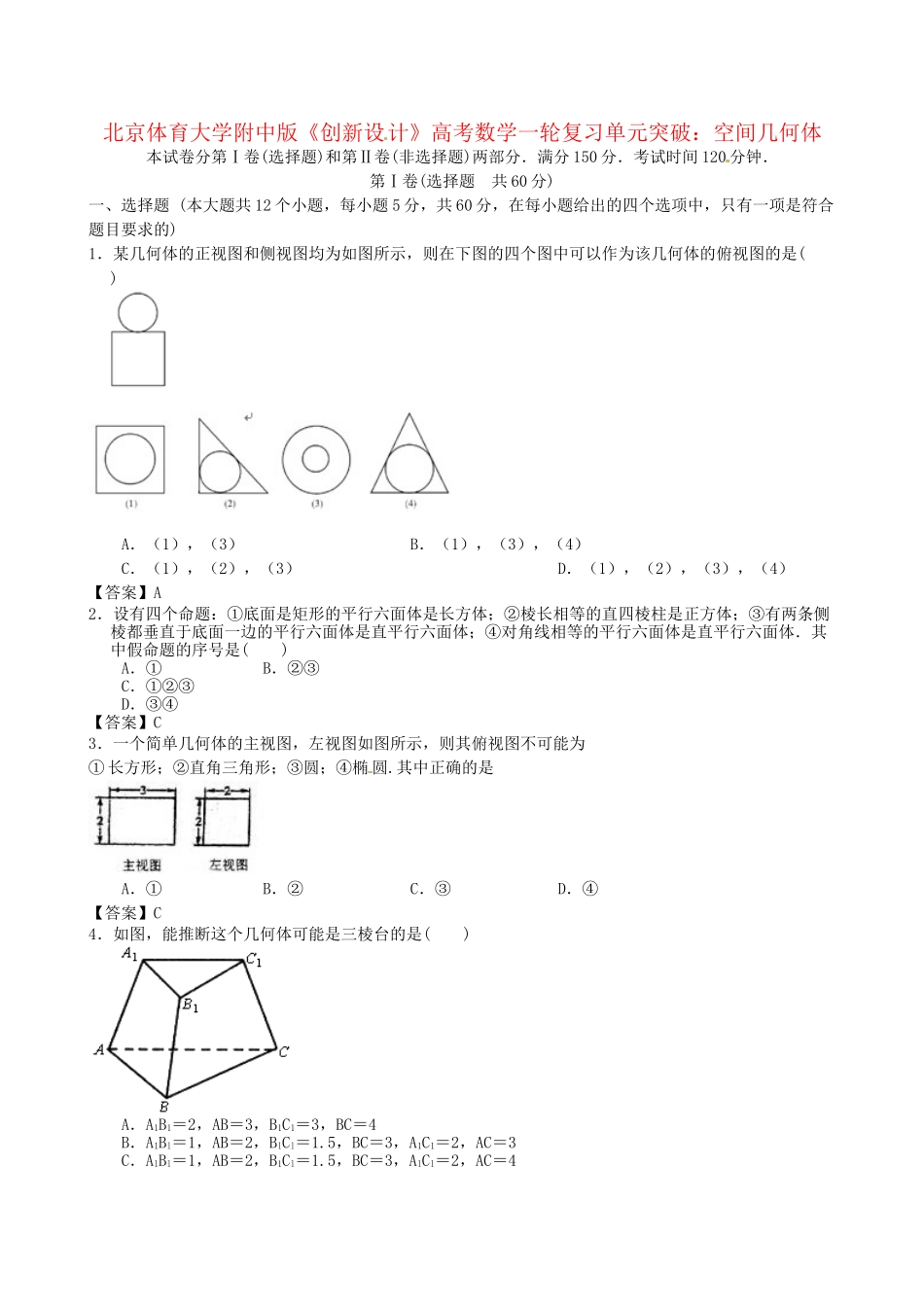
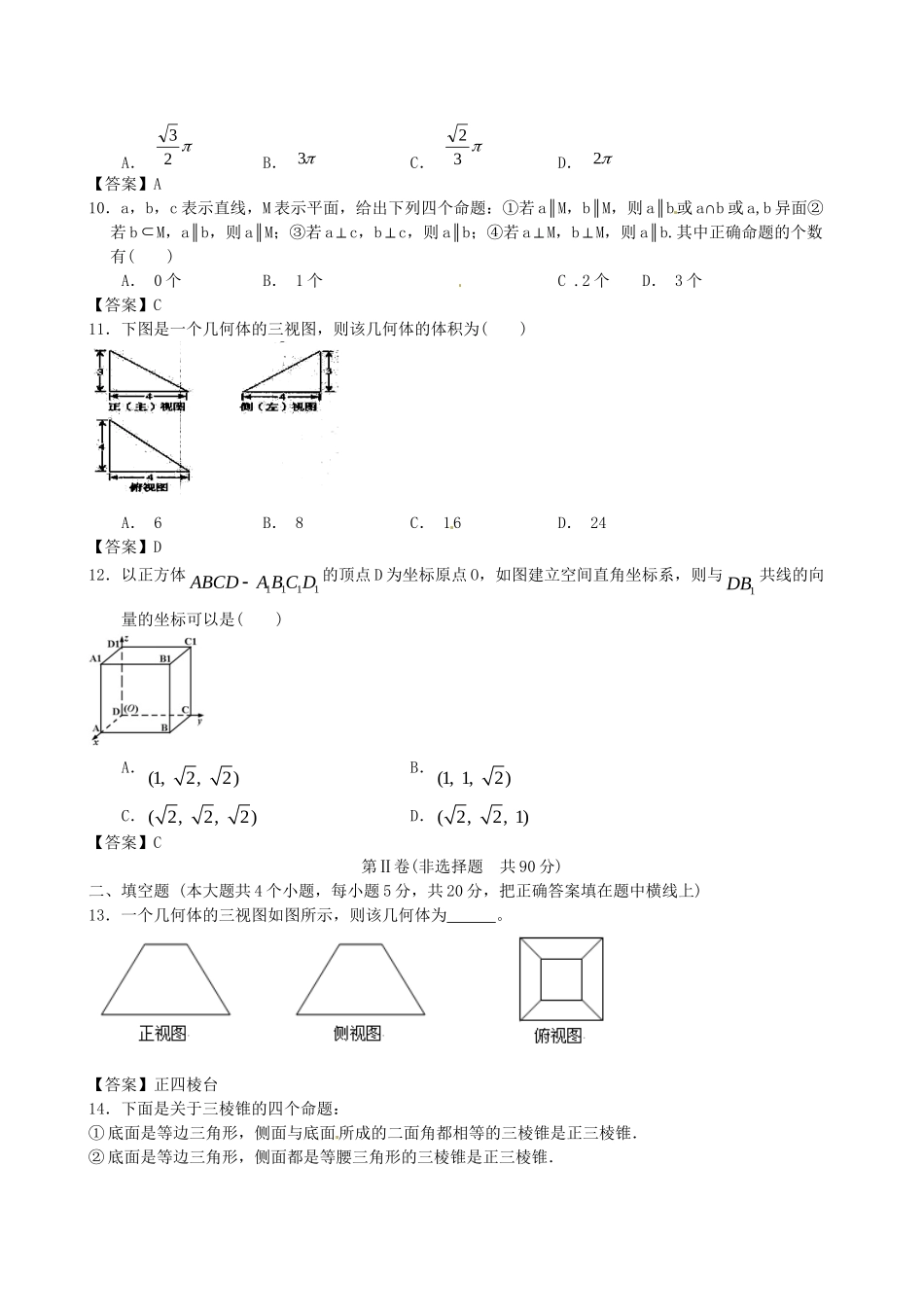
北京体育大学附中版《创新设计》高考数学一轮复习单元突破：空间几何体本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．某几何体的正视图和侧视图均为如图所示，则在下图的四个图中可以作为该几何体的俯视图的是()A．（1），（3）B．（1），（3），（4）C．（1），（2），（3）D．（1），（2），（3），（4）【答案】A2．设有四个命题：①底面是矩形的平行六面体是长方体；②棱长相等的直四棱柱是正方体；③有两条侧棱都垂直于底面一边的平行六面体是直平行六面体；④对角线相等的平行六面体是直平行六面体．其中假命题的序号是()A．①B．②③C．①②③D．③④【答案】C3．一个简单几何体的主视图，左视图如图所示，则其俯视图不可能为①长方形；②直角三角形；③圆；④椭圆.其中正确的是A．①B．②C．③D．④【答案】C4．如图，能推断这个几何体可能是三棱台的是()A．A1B1＝2，AB＝3，B1C1＝3，BC＝4B．A1Bl＝1，AB＝2，BlCl＝1.5，BC＝3，A1C1＝2，AC＝3C．AlBl＝1，AB＝2，B1Cl＝1.5，BC＝3，AlCl＝2，AC＝4D．AB＝A1B1，BC＝B1C1，CA＝C1A1【答案】C5．已知三角形的三边分别为cba,,，内切圆的半径为r，则三角形的面积为as(21rcb)；四面体的四个面的面积分别为4321,,,ssss，内切球的半径为R。类比三角形的面积可得四面体的体积为()A．RssssV)(214321B．RssssV)(314321C．RssssV)(414321D．RssssV)(4321【答案】B6．长度分别为1，a，a，a，a，a的线段能成为同一个四面体的6条棱的充要条件是()A．30aB．20aC．33aD．333a【答案】C7．下列命题中，正确的是()A．直线l⊥平面α，平面β∥直线l，则α⊥βB．平面α⊥β，直线m⊥β，则m∥αC．直线l是平面α的一条斜线，且l⊂β，则α与β必不垂直D．一个平面内的两条直线与另一个平面内的两条直线分别平行，则这两个平面平行【答案】A8．如图，一个空间几何体正视图与侧视图为全等的等边三角形，俯视图为一个半径为1的圆，那么这个几何体的全面积为()A．πB．3πC．2πD．π+3【答案】B9．如图，平面四边形ABCD中，1CDADAB，CDBDBD,2，将其沿对角线BD折成四面体BCDA'，使平面BDA'平面BCD，若四面体BCDA'顶点在同一个球面上，则该球的体积为()A．23B．3C．32D．2【答案】A10．a，b，c表示直线，M表示平面，给出下列四个命题：①若a∥M，b∥M，则a∥b或a∩b或a,b异面②若bM，a∥b，则a∥M；③若a⊥c，b⊥c，则a∥b；④若a⊥M，b⊥M，则a∥b.其中正确命题的个数有()A．0个B．1个C.2个D．3个【答案】C11．下图是一个几何体的三视图，则该几何体的体积为()A．6B．8C．16D．24【答案】D12．以正方体1111ABCDABCD的顶点D为坐标原点O，如图建立空间直角坐标系，则与1DB�共线的向量的坐标可以是()A．(1,2,2)B．(1,1,2)C．(2,2,2)D．(2,2,1)【答案】C第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．一个几何体的三视图如图所示，则该几何体为。【答案】正四棱台14．下面是关于三棱锥的四个命题：①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥．③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥．④侧棱与底面所成的角相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．其中，真命题的编号是(写出所有真命题的编号）【答案】①④15．直三棱柱111ABCABC的各顶点都在同一球面上，若12ABACAA，120BAC，则此球的表面积等于；【答案】2016．如图，一个三棱锥的三视图的轮廓都是边长为1的正方形，则此三棱锥外接球的表面积．【答案】3三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．如图，四棱锥PABCD的底面是正方形，PDABCD底面，点E在棱PB上.(Ⅰ）求证：平面AECPDB平面；(Ⅱ...