正弦函数性质课件-北师大版VIP免费

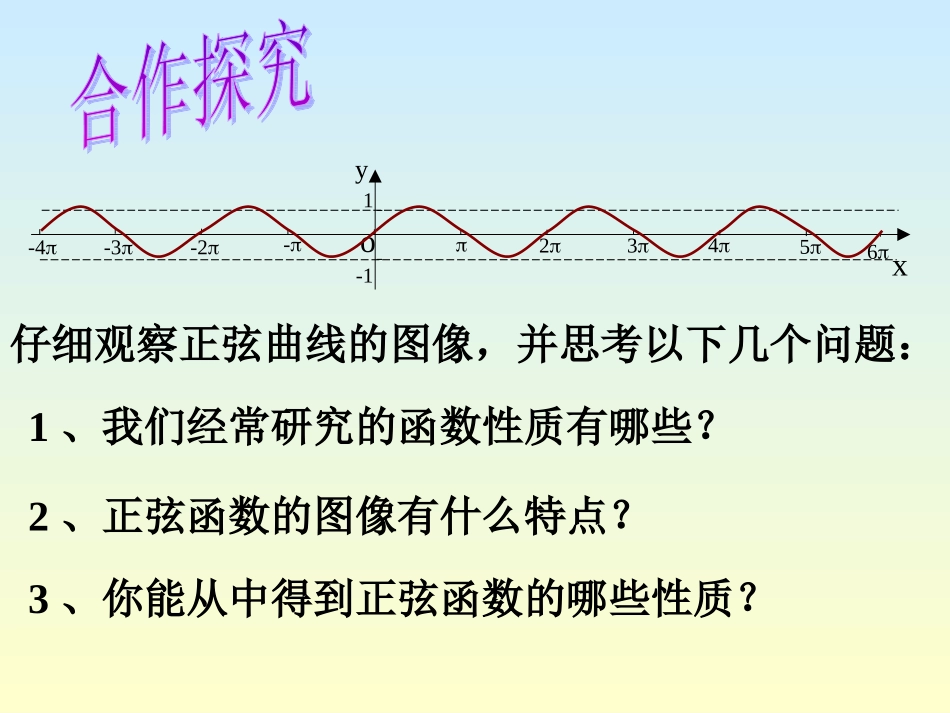
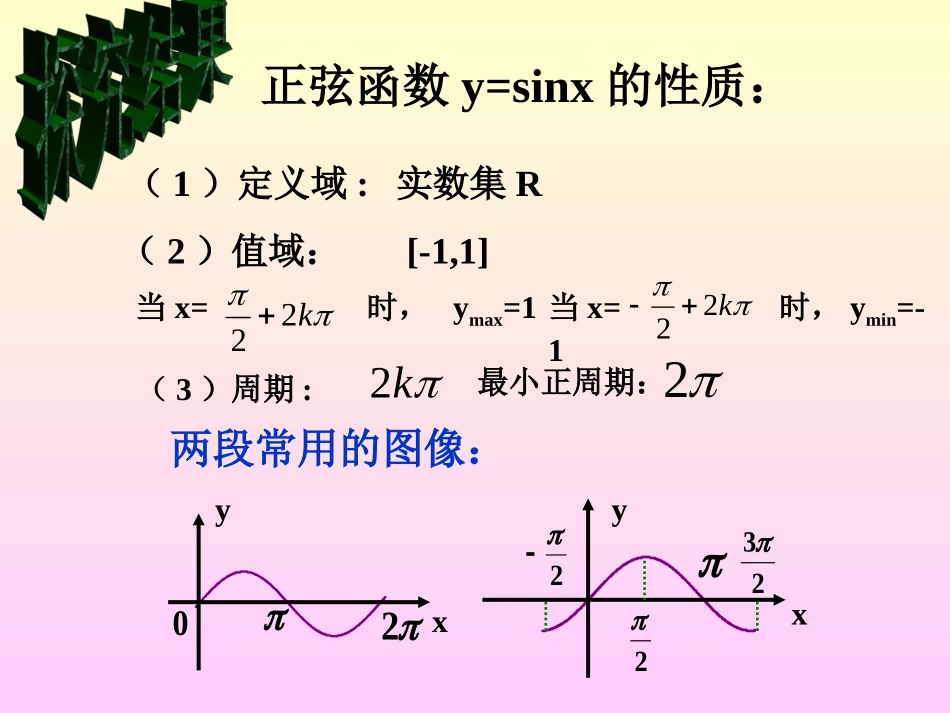
x6yo--12345-2-3-41仔细观察正弦曲线的图像，并思考以下几个问题：1、我们经常研究的函数性质有哪些？2、正弦函数的图像有什么特点？3、你能从中得到正弦函数的哪些性质？正弦函数y=sinx的性质：2（1）定义域:实数集R（2）值域：[-1,1]当x=时，ymin=-1当x=时，ymax=1（3）周期:最小正周期：k22k22k2两段常用的图像：02yx2223yx（4）正弦函数的单调性y=sinx(x)增区间为[，]其函数值从-1增至122xyo--1234-2-31223252722325减区间为[，]其函数值从1减至-1223Zkkk,22,22Zkkk,223,2223,2Rx（5）正弦函数的奇偶性y=sinxyxo--1234-2-31223252722325y=sinx(xR)图象关于原点对称sin(-x)=-sinx即f(-x)=-f(x)正弦函数为奇函数正弦曲线：sinyxxRxy1-1正弦曲线还有其它对称中心吗？有对称轴吗？如果有，请写出对称轴方程及对称中心的坐标，如果没有，请说明理由。对称轴：,2xkkZ对称中心：(,0)kkZ思考交流二、正弦函数性质的简单应用例1、不求值，比较下列各组正弦值的大小：)10sin()8sin()1与87sin85sin)2与分析：利用正弦函数的不同区间上的单调性进行比较。解：1）因为01082并且f(x)=sinx在上是增函数，所以2,2)10sin()8sin(2）因为87852并且f(x)=sinx在上是减函数，所以],2[87sin85sin)10sin()8sin()1与87sin85sin)2与例2、求函数y=4+sinx的最大值、最小值，并求这个函数取最大值、最小值的x值的集合。解：使y=4+sinx取得最大值的x的集合是：Zkkxx,22使y=4+sinx取得最小值的x的集合是：514sin4maxmaxxy3)1(4sin4minminxyZkkxx,221、观察正弦曲线，写出满足sinx>0的区间.2、函数y=2+sinx在区间＿＿＿＿＿＿＿上是增加的，在区间＿＿＿＿＿＿＿＿上是减少的；当x=＿＿＿＿＿＿＿时，y取最大值＿＿；当x=＿＿＿＿＿＿时，y取最小值＿＿。3、函数y=4sinx,当x[-∈π,π]时，在区间＿＿＿＿＿上是增加的，在区间＿＿＿＿＿＿＿＿＿＿是减少的；当x=______时，y取最大值__________；当x=_________时，y取最小值_______.）（Zkk,22Zkkk,22,22，和22,2Zkkk,223,22)(,232Zkk222，-4413(2kπ,2kπ+π)kZ∈当堂检测4不求值，比较下列各对正弦值的大小：（１）（２）260sin250sin与863sin754sin与解:(1)90250260270sin250sin260sin90,270yx并且在上是减函数1、正弦函数的性质2、正弦函数的性质的简单应用3、观察-发现-讨论-归纳的思想方法独立作业教材P28A组:2、3你懂了吗？