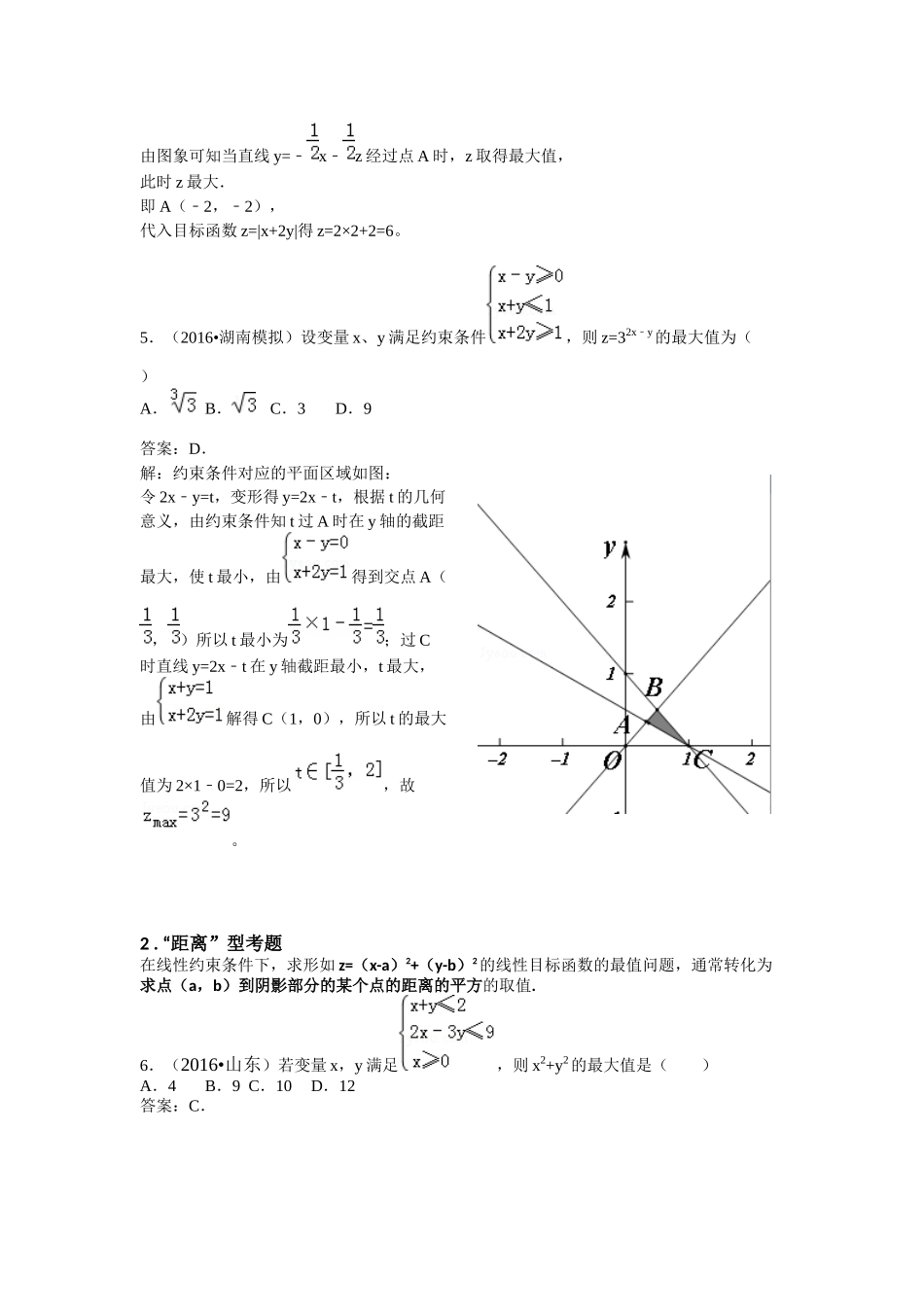
线性规划题型总结1.“截距”型考题在线性约束条件下,求形如的线性目标函数的最值问题,通常转化为求直线在轴上的截距的取值.结合图形易知,目标函数的最值一般在可行域的顶点处取得.掌握此规律可以有效避免因画图太草而造成的视觉误差.1.(2017•天津)设变量x,y满足约束条件,则目标函数z=x+y的最大值为()A.B.1C.D.3答案:D解:变量x,y满足约束条件的可行域如图:目标函数z=x+y结果可行域的A点时,目标函数取得最大值,由可得A(0,3),目标函数z=x+y的最大值为:3.2.(2017•新课标Ⅲ)若x,y满足约束条件,则z=3x4y﹣的最小值为.答案:﹣1.解:由z=3x4y﹣,得y=x﹣,作出不等式对应的可行域(阴影部分),平移直线y=x﹣,由平移可知当直线y=x﹣,经过点B(1,1)时,直线y=x﹣的截距最大,此时z取得最小值,将B的坐标代入z=3x4y=34=1﹣﹣﹣,即目标函数z=3x4y﹣的最小值为﹣1.3.(2017•浙江)若x、y满足约束条件,则z=x+2y的取值范围是()A.[0,6]B.[0,4]C.[6,+∞)D.[4,+∞)答案:D.解:x、y满足约束条件,表示的可行域如图:目标函数z=x+2y经过C点时,函数取得最小值,由解得C(2,1),目标函数的最小值为:4目标函数的范围是[4,+∞).4.(2016•河南二模)已知x,y∈R,且满足,则z=|x+2y|的最大值为()A.10B.8C.6D.3答案:C.解:作出不等式组,对应的平面区域如图:(阴影部分)由z=|x+2y|,平移直线y=﹣x+z,由图象可知当直线y=﹣x﹣z经过点A时,z取得最大值,此时z最大.即A(﹣2,﹣2),代入目标函数z=|x+2y|得z=2×2+2=6。5.(2016•湖南模拟)设变量x、y满足约束条件,则z=32xy﹣的最大值为()A.B.C.3D.9答案:D.解:约束条件对应的平面区域如图:令2xy=t﹣,变形得y=2xt﹣,根据t的几何意义,由约束条件知t过A时在y轴的截距最大,使t最小,由得到交点A(,)所以t最小为;过C时直线y=2xt﹣在y轴截距最小,t最大,由解得C(1,0),所以t的最大值为2×10=2﹣,所以,故。2.“距离”型考题在线性约束条件下,求形如z=(x-a)2+(y-b)2的线性目标函数的最值问题,通常转化为求点(a,b)到阴影部分的某个点的距离的平方的取值.6.(2016•山东)若变量x,y满足,则x2+y2的最大值是()A.4B.9C.10D.12答案:C.解:由约束条件作出可行域如图,A (0,﹣3),C(0,2),∴|OA|>|OC|,联立,解得B(3,﹣1). ,x∴2+y2的最大值是10.7.(2016•浙江)在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影,由区域中的点在直线x+y2=0﹣上的投影构成的线段记为AB,则|AB|=()A.2B.4C.3D.6答案:C解:作出不等式组对应的平面区域如图:(阴影部分),区域内的点在直线x+y2=0﹣上的投影构成线段R′Q′,即SAB,而R′Q′=RQ,由得,即Q(﹣1,1),由得,即R(2,﹣2),则|AB|=|QR|===3,8.(2016•安徽模拟)如果实数x,y满足,则z=x2+y22x﹣的最小值是()A.3B.C.4D.答案:B.解:由z=x2+y22x=﹣(x1﹣)2+y21﹣,设m=(x1﹣)2+y2,则m的几何意义是区域内的点到点D(1,0)的距离的平方,作出不等式组对应的平面区域如图:由图象知D到AC的距离为最小值,此时d==,则m=d2=()2=,则z=m1=﹣1=﹣。3.“斜率”型考题在线性约束条件下,求形如z=的线性目标函数的最值问题,通常转化为求过点(a,b)阴影部分的某个点的直线斜率的取值.9.(2016•唐山一模)若x,y满足不等式组,则的最大值是()A.B.1C.2D.3答案:C解:由题意作平面区域如下,的几何意义是阴影内的点(x,y)与原点的连线的斜率,结合图象可知,过点A(1,2)时有最大值,此时==2,10.(2016•莱芜一模)已知x,y满足约束条件,则z=的范围是()A.[,2]B.B[﹣,]C.[,]D.[,]答案:C解:画出满足条件的平面区域,如图示:,由,解得A(1,2),由,解得B(3,1),而z=的几何意义表示过平面区域内的点与(﹣1,﹣1)的直线的斜率,显然直线AC斜率最大,直线BC斜率最小,KAC==,KBC==.11.(2016•衡阳二模)已知变量x,y满足,则的取值范围是()A.B.C.D.答案:[,]解:作出满足所对应的区域(如图阴影),变形目...