模块综合测评(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∪B=()A.{1,2,4}B.{2,3,4}C.{0,2,4}D.{0,2,3,4}【解析】 全集U={0,1,2,3,4},集合A={1,2,3},∴∁UA={0,4},又B={2,4},则(∁UA)∪B={0,2,4}.故选C.【答案】C2.可作为函数y=f(x)的图象的是()【解析】由函数的定义可知:每当给出x的一个值,则f(x)有唯一确定的实数值与之对应,只有D符合.【答案】D3.同时满足以下三个条件的函数是()①图象过点(0,1);②在区间(0,+∞)上单调递减;③是偶函数.A.f(x)=-(x+1)2+2B.f(x)=3|x|C.f(x)=|x|D.f(x)=x-2【解析】A.若f(x)=-(x+1)2+2,则函数关于x=-1对称,不是偶函数,不满足条件③.B.若f(x)=3|x|,在区间(0,+∞)上单调递增,不满足条件②.C.若f(x)=|x|,则三个条件都满足.D.若f(x)=x-2,则f(0)无意义,不满足条件①.故选C.【答案】C4.下列函数中,与y=-3|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是()A.y=-B.y=|x|-C.y=-(2x+2-x)D.y=x3-1【解析】y=-3|x|为偶函数,在(-∞,0)上是增函数,对于选项A,D不是偶函数,B,C是偶函数;对于选项B,当x<0时,y=-x+是减函数;故答案选C.【答案】C5.函数f(x)=2x-1+log2x的零点所在区间是()A.B.C.D.(1,2)【解析】 函数f(x)=2x-1+log2x,∴f=-1,f(1)=1,∴f·f(1)<0,故连续函数f(x)的零点所在区间是,故选C.【答案】C6.若函数f(x)是幂函数,且=3,则f的值为()A.-3B.-C.3D.【解析】设f(x)=xα(α为常数),则==3【答案】D7.函数f(x)=+lg(3x+1)的定义域为()A.B.C.D.【解析】要使函数有意义,x应满足:解得-<x<1,故函数f(x)=+lg(3x+1)的定义域为.【答案】A8.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为()A.a
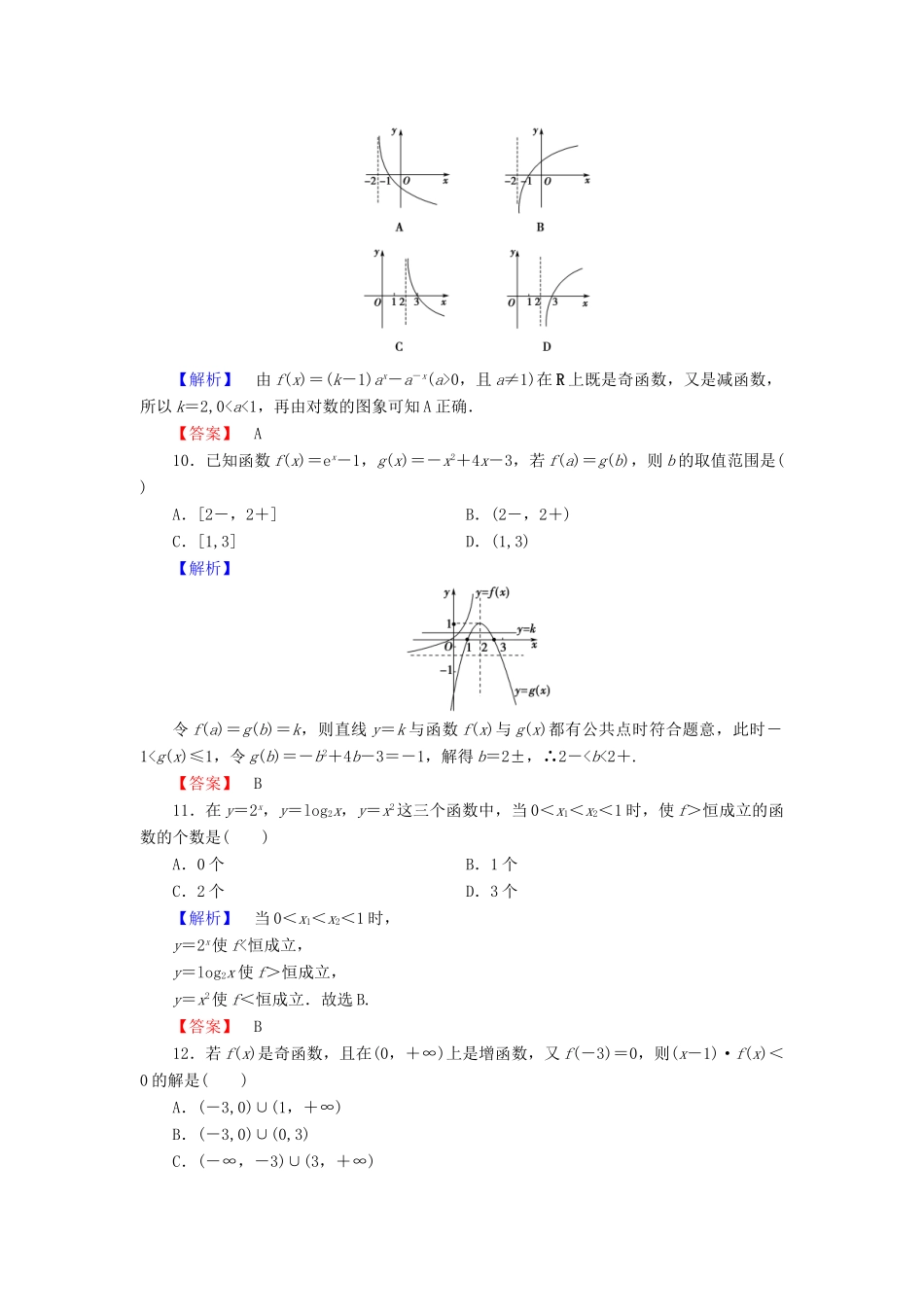
f(-log23)>f(0),即c0,且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x+k)的图象是()【解析】由f(x)=(k-1)ax-a-x(a>0,且a≠1)在R上既是奇函数,又是减函数,所以k=2,0b>1,若logab+logba=,ab=ba,则a=________,b=________.【解析】 logab+logba=logab+=,∴logab=2或. a>b>1,∴logab