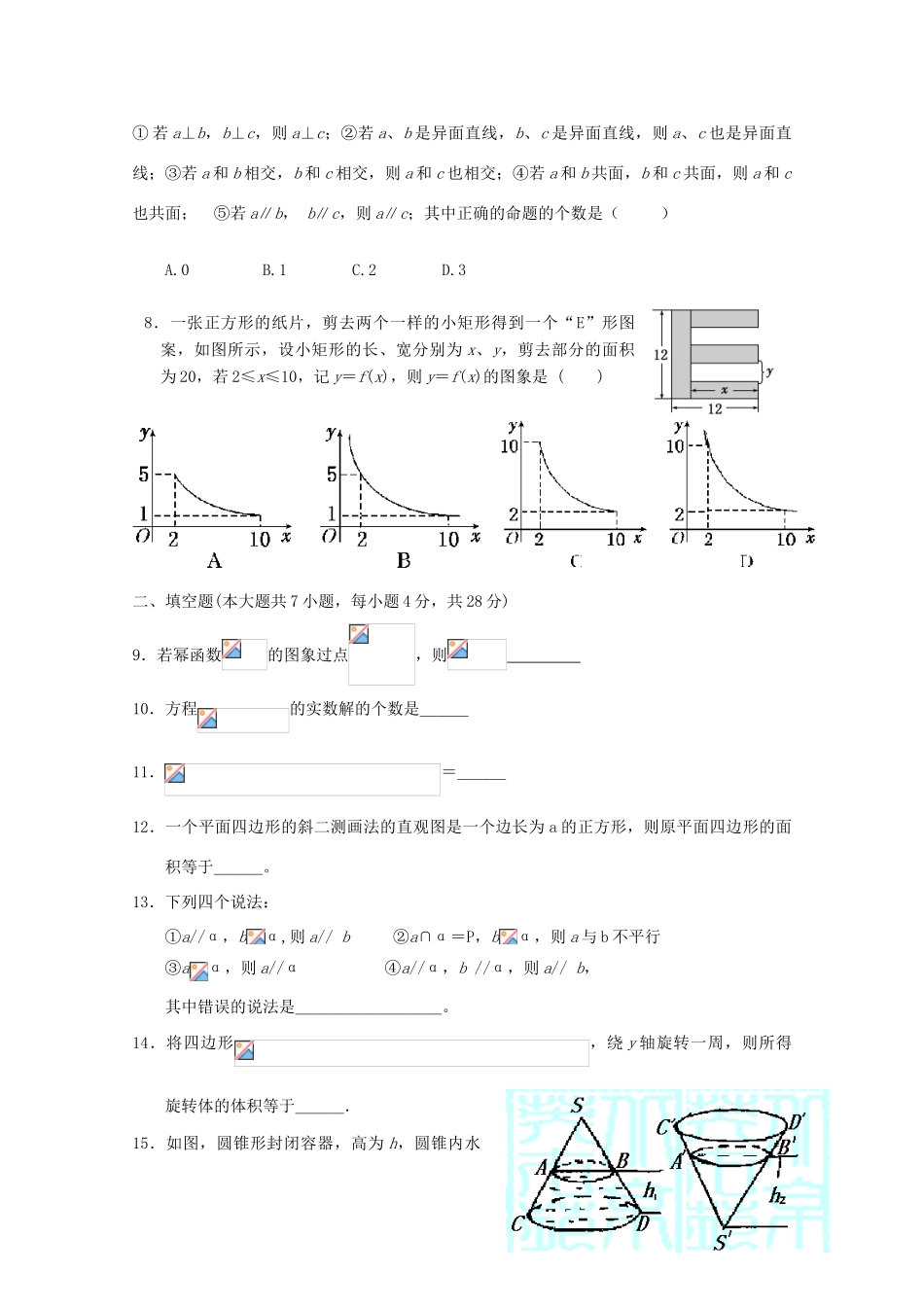
上学期高一数学11月月考试题08一、选择题(本大题共8小题,每小题3分,共24分)1.函数f(x)=的定义域为()A.B.(0,+)C.(0,1D.(0,1)2.下列函数中,同时具有性质:(1)图象过点(0,1);(2)在区间(0,+∞)上是减函数;(3)是偶函数.这样的函数是()A.y=x3+1B.y=log2(|x|+2)C.y=()|x|D.y=2|x|3.下列函数中没有零点的是()A、B、C、D、4.若函数的一个正零点附近的函数值的参考数据如下:那么方程的一个近似根(精确到0.1)为()A、1..2B、1.3C、1.4D、1.55.下列几何体中,正视图、侧视图、俯视图都相同的几何体的序号是()A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)6.将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了()A.B.12a2C.18a2D.24a27.设是空间的三条直线,给出以下五个命题:①若a⊥b,b⊥c,则a⊥c;②若a、b是异面直线,b、c是异面直线,则a、c也是异面直线;③若a和b相交,b和c相交,则a和c也相交;④若a和b共面,b和c共面,则a和c也共面;⑤若a∥b,b∥c,则a∥c;其中正确的命题的个数是()A.0B.1C.2D.38.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”形图案,如图所示,设小矩形的长、宽分别为x、y,剪去部分的面积为20,若2≤x≤10,记y=f(x),则y=f(x)的图象是()二、填空题(本大题共7小题,每小题4分,共28分)9.若幂函数的图象过点,则10.方程的实数解的个数是___11.=___12.一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于___。13.下列四个说法:①a//α,bα,则a//b②a∩α=P,bα,则a与b不平行③aα,则a//α④a//α,b//α,则a//b,其中错误的说法是_________。14.将四边形,绕y轴旋转一周,则所得旋转体的体积等于___.15.如图,圆锥形封闭容器,高为h,圆锥内水面高为若将圆锥倒置后,圆锥内水面高为三、解答题(本大题共6小题,共48分)16.(本题满分6分)已知集合M={x|x2-3x+2=0},N={},Q={1,a2+1,a+1}(1).求:MN;(2).若MQ,求实数a的值。17.(本题满分8分)设平面α∥β,两条异面直线AC和BD分别在平面α、β内,线段AB、CD中点分别为M、N,设MN=a,线段AC=BD=2a,求异面直线AC和BD所成的角.18.(本题满分8分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费200元.(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少αβABCDMN19.(本题满分8分)已知ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:AP∥GH、20.(本题满分8分)已知函数(1)求函数的定义域;(2)求函数的零点;(3)若函数f(x)的最小值为,求的值。21.(本题满分10分)已知函数f(x)=ax+(x≠0,常数a∈R).(1)讨论函数f(x)的奇偶性,并说明理由;(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.参考答案一、CCCCDBBA二、2①③④三、16.解:(1).M={1,2},N={0,1,2,3}……………………….1分MN={1,2}………………………………………………….3分(2).MQ当a2+1=2即a=1或-1时,a=1Q={1,2,2}(舍)a=1符合题意;……4分当a+1=2即a=1时,Q={1,1,1}(舍)……………………………..5分a=-1……………………………………………………………6分17.18.解:(Ⅰ)当每辆车的月租金定为3600元时,未租出的车辆数为,所以这时租出了88辆车.…………………….2分(Ⅱ)设每辆车的月租金定为x元,则租赁公司的月收益为,……………………4分整理得.所以,当x=4100时,最大,最大值为,……………….7分即当每辆车的月租金定为4100元时,租赁公司的月收益最大,最大月收益为304200元….8分19.证明:连结AC,设AC交BD于O,连结MO、 四边形ABCD是平行四边形,∴O是AC的中点、又M是PC的中点,∴MO∥PA、…………………….4分又MO面BDM、PA面BDM、∴PA∥面BDM、…………………….6分又经过PA与点G的平面交面BDM于GH、∴AP∥GH、………………...