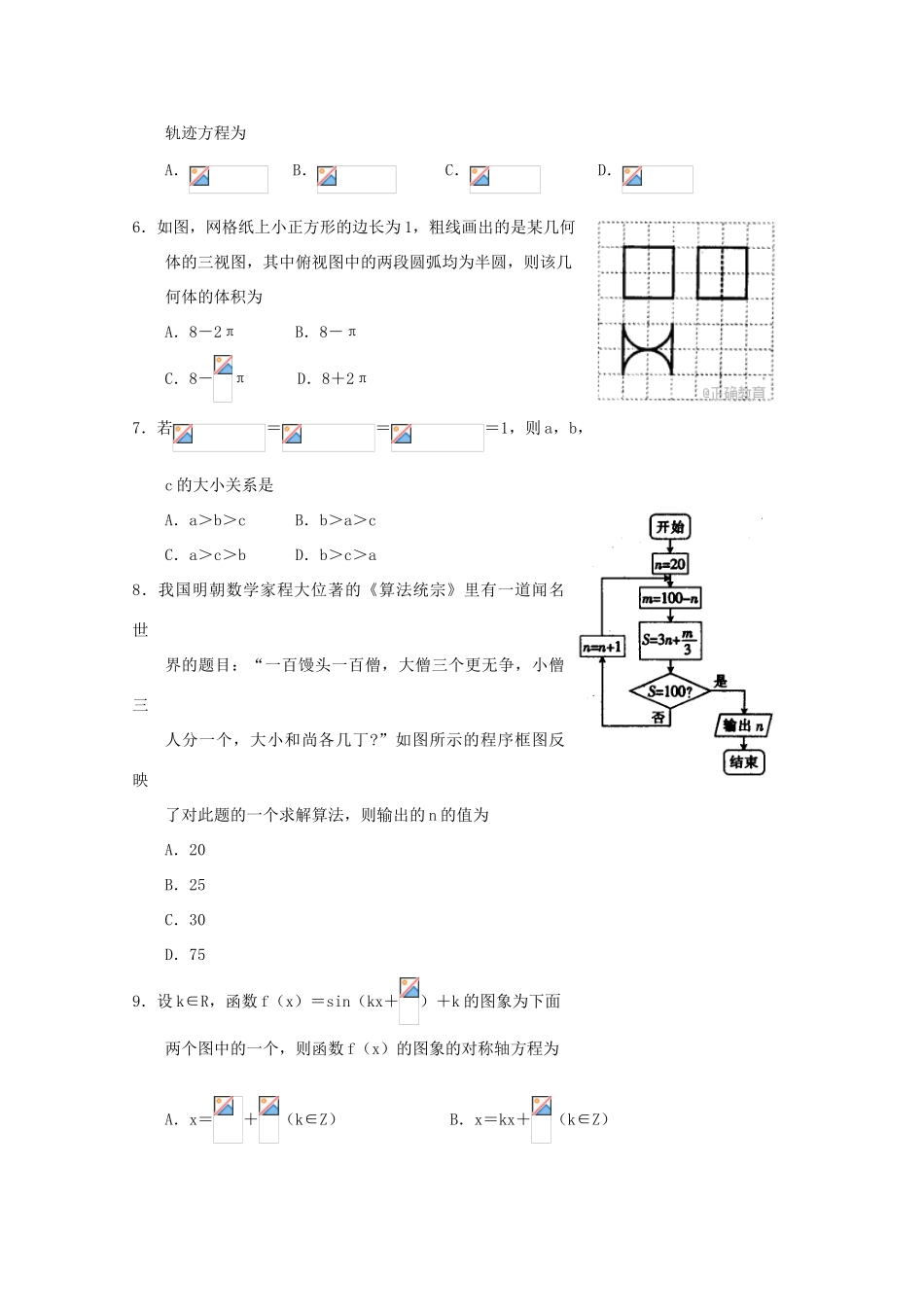
新乡市2018届高三年级第一次模拟测试数学试卷(理科)考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.2.请将各题答案填在答题卡上.3.本试卷主要考试内容:高考全部内容.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|-x≤0},B={x|a-1≤x<a},若A∩B只有一个元素,则a=A.0B.1C.2D.1或22.设复数z满足iz=|2+i|+2i,则|z|=A.3B.C.9D.103.点P(x,y)是如图所示的三角形区域(包括边界)内任意一点,则的最小值为A.—2B.—C.—D.—4.“a>1”是“(a∈R)的展开式中的常数项大于1”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件5.在平面直角坐标系xOy中,动点P关于x轴的对称点为Q,且·=2,则点P的轨迹方程为A.B.C.D.6.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图中的两段圆弧均为半圆,则该几何体的体积为A.8-2πB.8-πC.8-πD.8+2π7.若===1,则a,b,c的大小关系是A.a>b>cB.b>a>cC.a>c>bD.b>c>a8.我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”如图所示的程序框图反映了对此题的一个求解算法,则输出的n的值为A.20B.25C.30D.759.设k∈R,函数f(x)=sin(kx+)+k的图象为下面两个图中的一个,则函数f(x)的图象的对称轴方程为A.x=+(k∈Z)B.x=kx+(k∈Z)C.x=-(k∈Z)D.x=kπ-(k∈Z)10.抛物线M:=4x的准线与x轴交于点A,点F为焦点,若抛物线M上一点P满足PA⊥PF,则以F为圆心且过点P的圆被y轴所截得的弦长约为(参考数据:≈2.24)A.B.C.D.11.在三棱锥D—ABC中,CD⊥底面ABC,AE∥CD,△ABC为正三角形,AB=CD=AE=2,三棱锥D—ABC与三棱锥E—ABC的公共部分为一个三棱锥,则此三棱锥的外接球的表面积为A.πB.6πC.πD.π12.△ABC的内角A,B,C的对边分别为a,b,c,已知=acosA—ccosB+,且b=2,则a的最小值为A.B.C.D.第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卷中的横线上.13.已知向量a,b满足|b|=2|a|=2,a与b的夹角为120°,则|a-2b|=_____________.14.若2tanα=tan420°,则tan(α+)=_____________.15.在一次53.5公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示.若用简单随机抽样方法从中选取2人,则这2人成绩的平均数恰为100的概率为_______________.16.若函数f(x)=恰有3个零点,则f(a)的取值范围为_______________.三、解答题:共70分.解答应写出文字说明.证明过程或演算步骤.第17~21题为必考题.每个试题考生都必须作答.第22、23题为选考题.考生根据要求作答.(一)必考题:共60分.17.(12分)已知为等差数列{}的前n项和,且a17=33,S7=49.(1)证明:a1,a5,a41成等比数列;(2)求数列{·}的前n项和.18.(12分)已知某智能手机制作完成之后还需要依次通过三道严格的检测程序,第一道检测、第二道检测、第三道检测通过的概率分别为,,,每道程序是相互独立的,且一旦检测不通过就停止检测,每部手机只有三道程序都通过才能出厂销售.(1)求检测过程中只通过两道程序的概率;(2)现有3部该智能手机进入检测,记这3部手机可以出厂销售的部数为X,求X的分布列及数学期望.19.(12分)如图,在四棱锥E—ABCD中,底面为等腰梯形,且底面与侧面ABE垂直,AB∥CD,F,G,M分别为线段BE,BC,AD的中点,AE=CD=1,AD=2,AB=3,且AE⊥AB.(1)证明:MF∥平面CDE;(2)求EG与平面CDE所成角的正弦值.20.(12分)已知椭圆C:(a>b>0)经过(0,),且椭圆C的离心率为.(1)求椭圆C的方程;(2)设斜率存在的直线l与椭圆C交于P,Q两点,O为坐标原点,OP⊥OQ,且l与圆心为O的定圆W相切.直线:y=-x+n(n≠0)与圆W交于M,N两点,G(3,-3).求△GMN的面积的最...