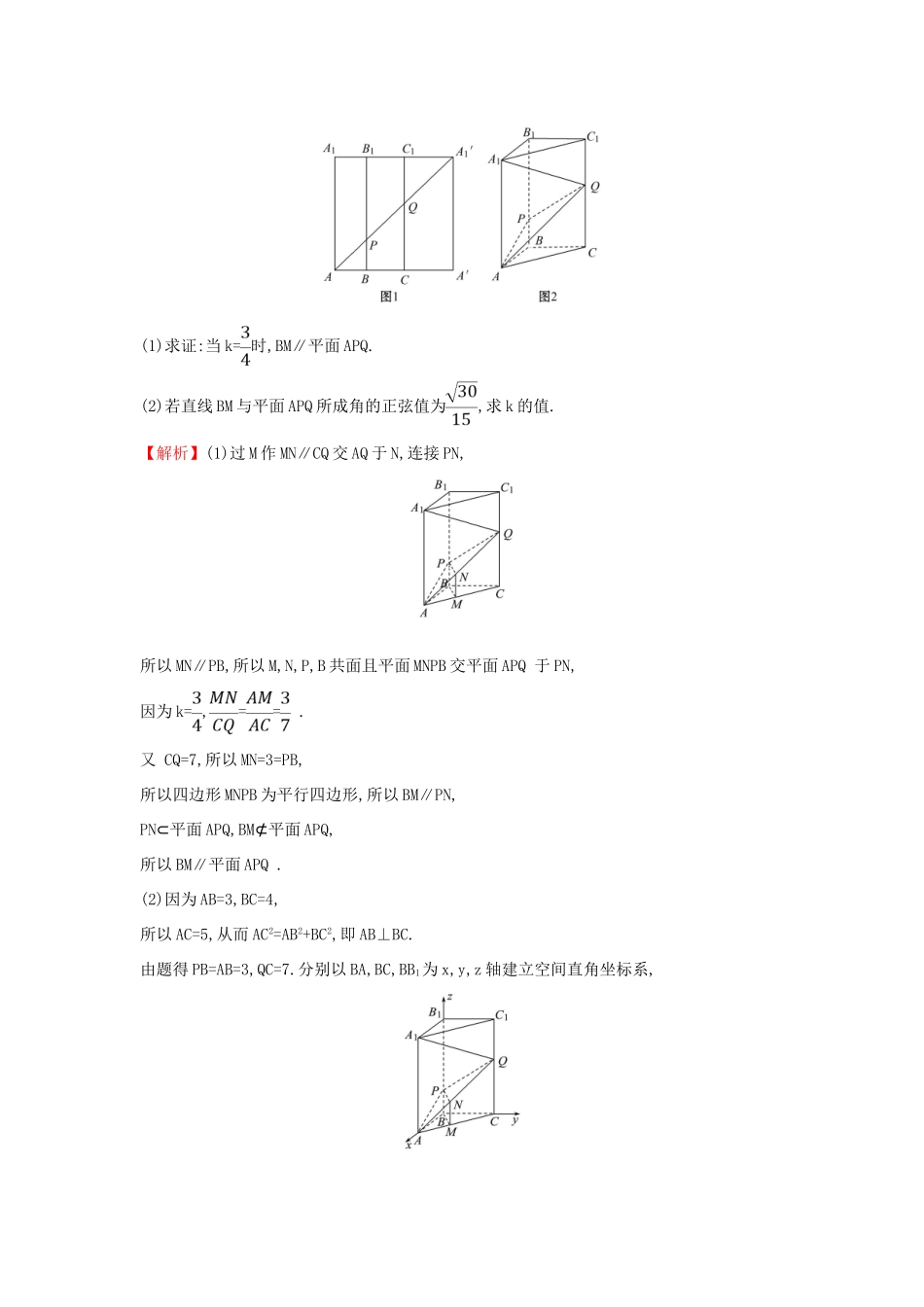
高考大题标准练(二)满分60分,实战模拟,60分钟拿到高考主观题高分!1.Sn为数列{an}的前n项和,已知3Sn+2=4an,bn·loan·loan+1=1.(1)求{an}的通项公式.(2)若数列{bn}的前n项和Tn满足Tn+k<0,求实数k的取值范围.【解析】(1)由3Sn+2=4an,可知3Sn+1+2=4an+1,两式相减可得3an+1=4an+1-4an,易知an≠0,于是=4.又3a1+2=4a1,得a1=2.所以{an}是首项为2,公比为4的等比数列,通项公式为an=22n-1.(2)由an=22n-1可知bn===.于是Tn=-++…+=.不等式Tn+k<0可化为k<-.因为n∈N*,所以->-,故k≤-.因此实数k的取值范围为.2.已知如图1所示,在边长为12的正方形AA′A1′A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1′分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A′1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1,在该三棱柱底边AC上有一点M,满足AM=kMC(0
0,得到m2<8,AB的垂直平分线方程为y-m=-(x-2),令y=0,得x=4,所以G(4,0),=(x1-4,y1),=(x2-4,y2),因为·=5,所以(x1-4)(x2-4)+y1y2=5.x1x2-4(x1+x2)+16+y1y2=5,-4×4+16+y1y2=5③,把②代入③得(m2-4)2+8(m2-4)-20=0,(m2+6)(m2-6)=0,m2=6<8,m=±,所以,直线l的方程为2x-y+2=0或2x+y+2=0.5.已知函数f(x)=ex+e-x,其中e是自然对数的底数.(1)若关于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求实数m的取值范围.(2)已知正数a满足:存在x0∈[1,+∞),使得f(x0)