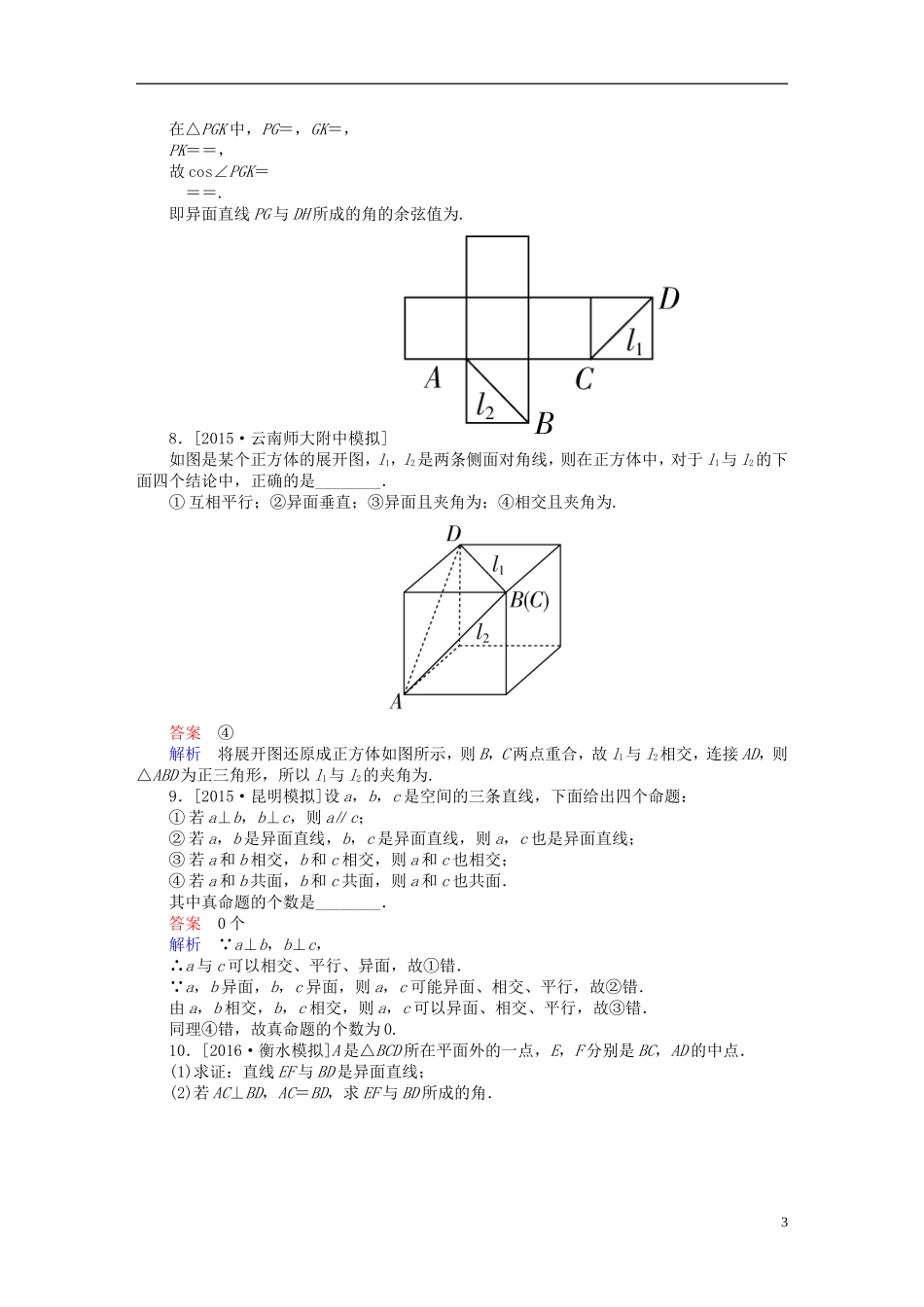
7-3空间点、直线、平面的位置关系练习文[A组·基础达标练]1.[2015·广东高考]若空间中n个不同的点两两距离都相等,则正整数n的取值()A.至多等于3B.至多等于4C.等于5D.大于5答案B解析首先我们知道正三角形的三个顶点满足两两距离相等,于是可以排除C、D.又注意到正四面体的四个顶点也满足两两距离相等,于是排除A,故选B.2.[2015·福建高考]若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案B解析由“m⊥α且l⊥m”推出“l⊂α或l∥α”,但由“m⊥α且l∥α”可推出“l⊥m”,所以“l⊥m”是“l∥α”的必要而不充分条件,故选B.3.[2016·威海模拟]设A、B、C、D是空间中四个不同的点,下列命题中,不正确的是()A.若AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若AB=AC,DB=DC,则AD=BCD.若AB=AC,DB=DC,则AD⊥BC答案C解析若AB=AC,DB=DC,AD不一定等于BC,故C不正确.4.[2015·海口模拟]已知正方体ABCD-A1B1C1D1中,O是BD1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是()A.A1、M、O三点共线B.M、O、A1、A四点共面C.A、O、C、M四点共面D.B、B1、O、M四点共面答案D解析由正方体的性质知,O也是A1C的中点,因此A1、M、O三点共线,又直线与直线外一点确定一个平面,所以B、C正确.由BB1与A1C异面知D错误.故选D.5.给出下列命题,其中正确命题的个数是()①如果线段AB在平面α内,那么直线AB在平面α内;②两个不同的平面可以相交于不在同一直线上的三个点A、B、C;③若三条直线a,b,c互相平行且分别交直线l于A,B,C三点,则这四条直线共面;④若三条直线两两相交,则这三条直线共面;⑤两组对边相等的四边形是平行四边形.A.1B.2C.3D.4答案B解析显然①③正确.若两平面有三个不共线的公共点,则这两平面重合,故②不正确.三条直线两两相交于同一点时,三条直线不一定共面,故④不正确;两组对边相等的四边形可能是空间四边形,⑤不正确.故选B.6.[2016·武汉模拟]如果两条异面直线称为“一对”,那么在正方体的十二条棱中共有异面直线()A.12对B.24对C.36对D.48对1答案B解析如图所示,与AB异面的直线有B1C1,CC1,A1D1,DD1四条,因为各棱具有相同的位置且正方体共有12条棱,共有异面直线=24(对).故选B.7.如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为________.答案解析折成的正四面体,如图,连接HE,取HE的中点K,连接GK,PK.则GK∥DH,故∠PGK(或其补角)即为所求的异面直线所成的角.设这个正四面体的棱长为2,2在△PGK中,PG=,GK=,PK==,故cos∠PGK===.即异面直线PG与DH所成的角的余弦值为.8.[2015·云南师大附中模拟]如图是某个正方体的展开图,l1,l2是两条侧面对角线,则在正方体中,对于l1与l2的下面四个结论中,正确的是________.①互相平行;②异面垂直;③异面且夹角为;④相交且夹角为.答案④解析将展开图还原成正方体如图所示,则B,C两点重合,故l1与l2相交,连接AD,则△ABD为正三角形,所以l1与l2的夹角为.9.[2015·昆明模拟]设a,b,c是空间的三条直线,下面给出四个命题:①若a⊥b,b⊥c,则a∥c;②若a,b是异面直线,b,c是异面直线,则a,c也是异面直线;③若a和b相交,b和c相交,则a和c也相交;④若a和b共面,b和c共面,则a和c也共面.其中真命题的个数是________.答案0个解析 a⊥b,b⊥c,∴a与c可以相交、平行、异面,故①错. a,b异面,b,c异面,则a,c可能异面、相交、平行,故②错.由a,b相交,b,c相交,则a,c可以异面、相交、平行,故③错.同理④错,故真命题的个数为0.10.[2016·衡水模拟]A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.(1)求证:直线EF与BD是异面直线;(2)若AC⊥BD,AC=BD,求EF与BD所成的角.3解(1)证明:假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内...