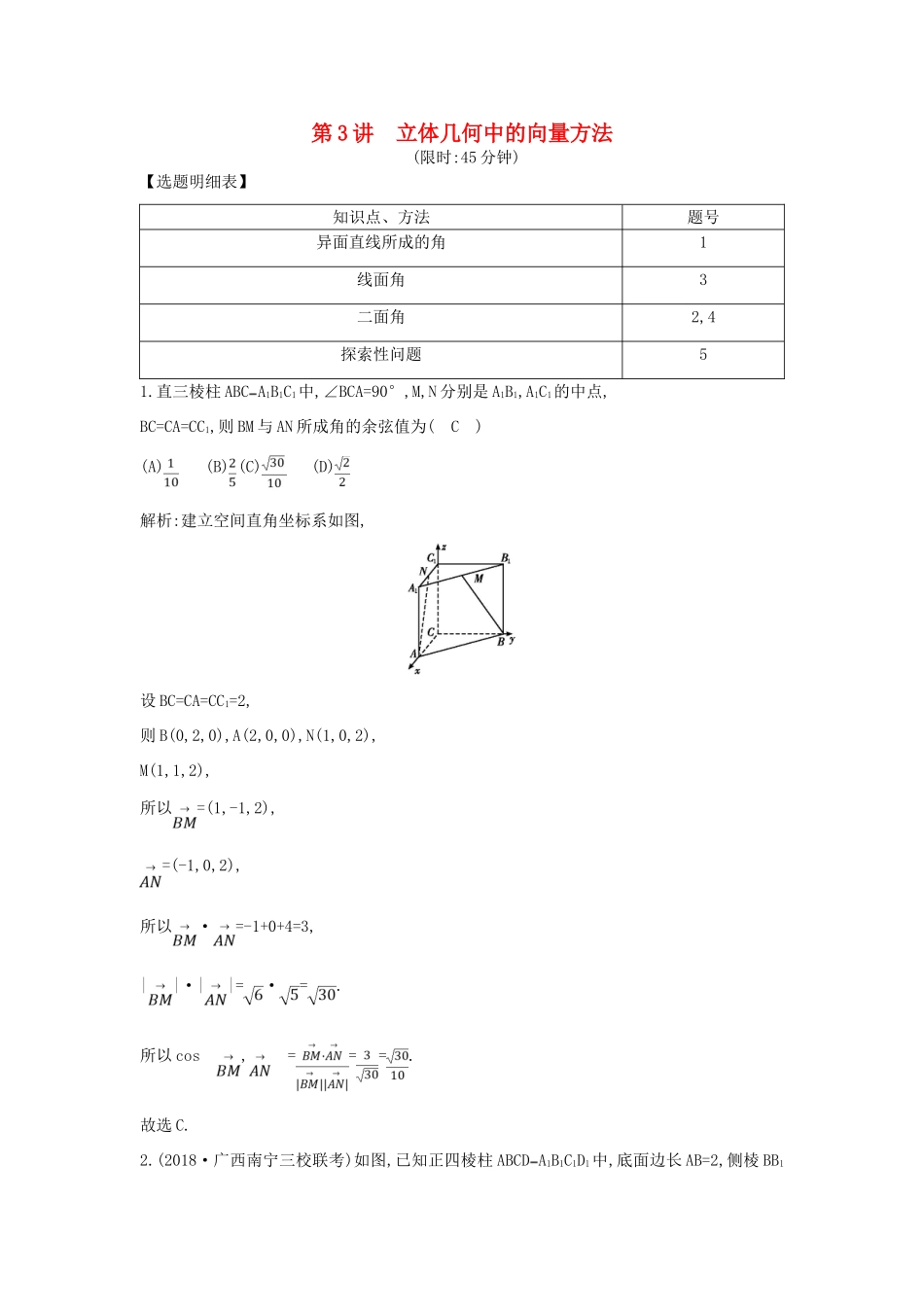
第3讲立体几何中的向量方法(限时:45分钟)【选题明细表】知识点、方法题号异面直线所成的角1线面角3二面角2,4探索性问题51.直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为(C)(A)(B)(C)(D)解析:建立空间直角坐标系如图,设BC=CA=CC1=2,则B(0,2,0),A(2,0,0),N(1,0,2),M(1,1,2),所以=(1,-1,2),=(-1,0,2),所以·=-1+0+4=3,||·||=·=.所以cos,===.故选C.2.(2018·广西南宁三校联考)如图,已知正四棱柱ABCDA1B1C1D1中,底面边长AB=2,侧棱BB1的长为4,过点B作B1C的垂线交侧棱CC1于点E,交B1C于点F.(1)求证:A1C⊥平面BDE;(2)求二面角EBDA1的余弦值.(1)证明:连接AC,因为ABCDA1B1C1D1是正四棱柱,所以⇒BD⊥平面A1ACBD⊥A⇒1C.同理可得BE⊥⇒平面A1B1CBE⊥A⇒1C.又因为BD∩BE=B,所以A1C⊥平面BDE.(2)解:以DA,DC,DD1分别为x,y,z轴,建立空间直角坐标系,设CE=a,则B(2,2,0).E(0,2,a),B1(2,2,4),C(0,2,0),A1(2,0,4),由BE⊥B1C⇒·=0a=1,⇒所以E(0,2,1).设平面DBE的法向量为n=(x,y,z).由n⊥(x,y,z)⇒·(2,2,0)=0,所以x+y=0.由n⊥(x,y,z)⇒·(0,2,1)=0,所以2y+z=0.令y=1,得x=-1,z=-2,所以n=(-1,1,-2).设平面DBA1的法向量为m=(x1,y1,z1).由m⊥x⇒1+y1=0,由m⊥x⇒1+2z1=0,令x1=2得y1=-2,z1=-1,所以m=(2,-2,-1).设m与n所成的角为θ,则cosθ====-.由题意,二面角A1DBE为锐角,所以二面角A1DBE的余弦值为.3.(2018·郑州市一中入学测试)在如图所示的多面体中,四边形ABCD是平行四边形,四边形BDEF是矩形,ED⊥平面ABCD,∠ABD=,AB=2AD.(1)求证:平面BDEF⊥平面ADE;(3)若ED=BD,求直线AF与平面AEC所成角的正弦值.(1)证明:在△ABD中,∠ABD=,AB=2AD,由余弦定理,得BD=AD,从而BD2+AD2=AB2,故BD⊥AD,所以△ABD为直角三角形且∠ADB=90°.因为DE⊥平面ABCD,BD⊂平面ABCD,所以DE⊥BD.又AD∩DE=D,所以BD⊥平面ADE.因为BD⊂平面BDEF,所以平面BDEF⊥平面ADE.(2)解:由(1)可得,在Rt△ABD中,∠BAD=,BD=AD,又由ED=BD,设AD=1,则BD=ED=.因为DE⊥平面ABCD,BD⊥AD,所以,以点D为坐标原点,DA,DB,DE所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.则A(1,0,0),C(-1,,0),E(0,0,),F(0,,),所以=(-1,0,),=(-2,,0).设平面AEC的法向量为n=(x,y,z),则即令z=1,得n=(,2,1),为平面AEC的一个法向量.因为=(-1,,),所以cos==.所以直线AF与平面AEC所成角的正弦值为.4.(2018·广东省广州市海珠区一模)如图,四棱锥PABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AD=2BC=2,∠BAD=∠ABC=90°.(1)证明:PC⊥BC;(2)若直线PC与平面PAD所成角为30°,求二面角BPCD的余弦值.(1)证明:取AD的中点为O,连接PO,CO,因为△PAD为等边三角形,所以PO⊥AD.底面ABCD中,可得四边形ABCO为矩形,所以CO⊥AD,因为PO∩CO=O,所以AD⊥平面POC,PC⊂平面POC,AD⊥PC.又AD∥BC,所以PC⊥BC.(2)解:由平面PAD⊥平面ABCD,PO⊥AD知,所以PO⊥平面ABCD,OP,OD,OC两两垂直,直线PC与平面PAD所成角为30°,即∠CPO=30°,由AD=2,知PO=,得CO=1.分别以,,的方向为x轴、y轴、z轴的正方向建立空间直角坐标系Oxyz,则P(0,0,),D(0,1,0),C(1,0,0),B(1,-1,0),=(0,1,0),=(1,0,-),=(-1,1,0),设平面PBC的法向量为n=(x,y,z),所以则n=(,0,1),设平面PDC的法向量为m=(x1,y1,z1),所以则m=(,,1),cos===,所以可知二面角BPCD的余弦值为-.5.(2018·南昌市重点中学一模)如图,在三棱柱ABCDEF中,所有棱长均相等,且∠ABE=∠ACF=,CE∩BF=O,点P为线段ED上的动点(异于E,D两点).(1)当P为线段ED的中点时,证明:OP∥平面ACFD;(2)当P在线段ED上何处时,二面角OPFE的余弦值为?(1)证明:法一当P为ED的中点时,连接CD,因为O为CE的中点,所以OP∥CD,又OP⊄平面ACFD,CD⊂平面ACFD,所以OP∥平面ACFD.法二取EF的中点G,因为P为ED的中点,所以PG∥FD,又PG⊄平面ACFD,FD⊂平面ACFD,所以PG∥平面ACFD.连接OG,同理可证OG∥平面ACFD.故平面OPG∥平面ACFD.又OP⊂平面OPG,所以OP∥平面ACFD.(2)解:连接AE,AF,AO,令AB=,因为∠ABE=∠ACF=,所以AB=AC=AF=AE.又O为BF,CE的中点,所以AO⊥BF,AO⊥CE,所以AO⊥平面CBEF,又BC⊂平面CBEF,所以AO⊥BC,取BC的中点S,连接AS,OS,易知BC⊥AS,所以BC⊥平面ASO,所以BC⊥OS,又易知OS∥CF,所以BC⊥CF,故底面BCFE为正方形.以OB,OE,OA所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则O(0,0,0),B(1,0,0),E(0,1,0),F(-1,0,0),A(0,0,1),=(-1,0,0),=(-1,1,0),由=,得D(-1,1,1),令=t(0|=||=,得t=,故||=||,即当点P为DE的靠近点D的四等分点时,二面角OPFE的余弦值为.