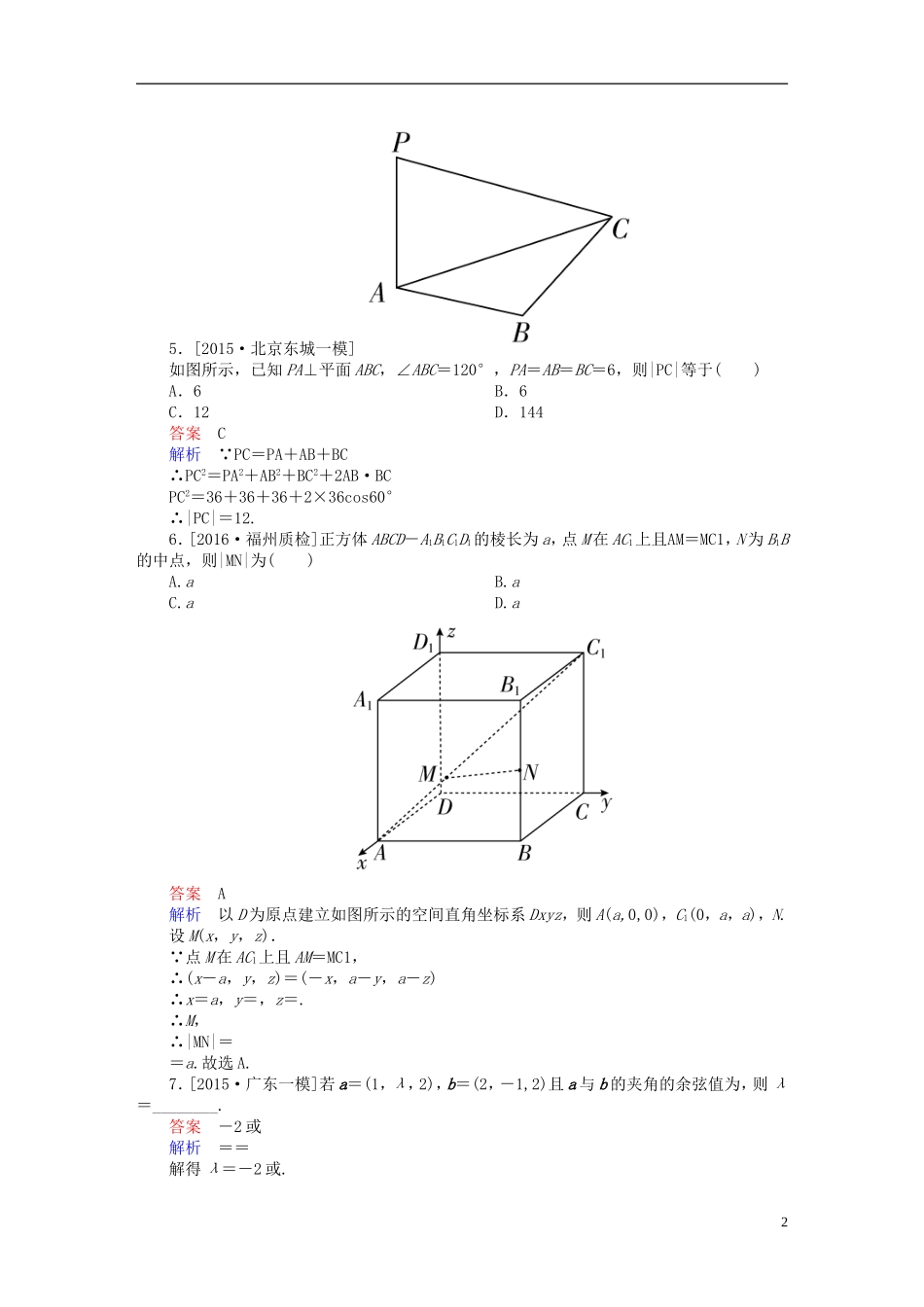
第七章立体几何7.6空间向量及运算练习理[A组·基础达标练]1.[2016·潍坊月考]如图所示,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos〈DP,AE〉=,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为()A.(1,1,1)B.C.D.(1,1,2)答案A解析设P(0,0,z),依题意知A(2,0,0),B(2,2,0),则E,于是DP=(0,0,z),AE=,cos〈DP,AE〉===.解得z=±2,由题图知z=2,故E(1,1,1).2.[2015·青岛一模]已知a=(-2,-3,1),b=(2,0,4),c=(-4,-6,2),则下列结论正确的是()A.a∥c,b∥cB.a∥b,a⊥cC.a∥c,a⊥bD.以上都不对答案C解析 c=2a,∴a∥c又a·b=(-2,-3,1)·(2,0,4)=0,故a⊥b,故选C.3.[2016·银川质检]已知a=(λ+1,0,2),b=(6,2μ-1,2λ),若a∥b,则λ与μ的值可以是()A.2,B.-,C.-3,2D.2,2答案A解析 a∥b可得解得或.4.已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a、b、c三向量共面,则实数λ等于()A.B.C.D.答案D解析由题意存在实数x,y使得c=xa+yb,即(7,5,λ)=x(2,-1,3)+y(-1,4,-2),由此得方程组解得x=,y=,所以λ=-=.15.[2015·北京东城一模]如图所示,已知PA⊥平面ABC,∠ABC=120°,PA=AB=BC=6,则|PC|等于()A.6B.6C.12D.144答案C解析 PC=PA+AB+BC∴PC2=PA2+AB2+BC2+2AB·BCPC2=36+36+36+2×36cos60°∴|PC|=12.6.[2016·福州质检]正方体ABCD-A1B1C1D1的棱长为a,点M在AC1上且AM=MC1,N为B1B的中点,则|MN|为()A.aB.aC.aD.a答案A解析以D为原点建立如图所示的空间直角坐标系Dxyz,则A(a,0,0),C1(0,a,a),N.设M(x,y,z). 点M在AC1上且AM=MC1,∴(x-a,y,z)=(-x,a-y,a-z)∴x=a,y=,z=.∴M,∴|MN|==a.故选A.7.[2015·广东一模]若a=(1,λ,2),b=(2,-1,2)且a与b的夹角的余弦值为,则λ=________.答案-2或解析==解得λ=-2或.28.已知A(4,1,3),B(2,3,1),C(3,7,-5),点P(x,-1,3)在平面ABC内,则x=________.答案11解析根据共面向量定理设AP=λAB+μAC,即(x-4,-2,0)=λ(-2,2,-2)+μ(-1,6,-8),由此得解得λ=-4,μ=1.所以x=4+8-1=11.9.[2015·新乡一模]在空间直角坐标系中,以点A(4,1,9)、B(10,-1,6)、C(x,4,3)为顶点的△ABC是以BC为斜边的等腰直角三角形,则实数x的值为________.答案2解析AB=(6,-2,-3),AC=(x-4,3,-6),由题意可知AB·AC=0.|AB|=|AC|,6(x-4)-6+18=0可解得x=2.10.已知各个面都是平行四边形的四棱柱ABCD-A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶NC′=3∶1,设MN=αAB+βAD+γAA′,试求α,β,γ之值.解MN=MB+BN=DB+BC′=(DA+AB)+(BC+CC′)=(-AD+AB)+(AD+AA′)=AB+AD+AA′,所以α=,β=,γ=.[B组·能力提升练]1.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k的值是()A.-1B.C.D.答案D解析由题意得(ka+b)·(2a-b)=0,即2ka2+(2-k)a·b-b2=0,即4k-5+(2-k)×(-1)=0,解得k=,故选D.2.已知矩形ABCD,AB=1,BC=,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中()A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直3答案B解析如图所示,在图(1)中,易知AE=CF=,BE=EF=FD=.在图(2)中,设AE=a,EF=b,FC=c,则〈a,b〉=〈b,c〉=90°,设〈a,c〉=θ,则AC=a+b+c,BD=3b,故AC·BD=3b2=1≠0,故AC与BD不垂直,A不正确;AB=AE+EB=a-b,CD=CF+FD=b-c,所以AB·CD=-a·c-b2=-cosθ-.当cosθ=-,即θ=时,AB·CD=0,故B正确;AD=AE+ED=a+2b,BC=BF+FC=2b+c,所以AD·BC=a·c+4b2=cosθ+=(cosθ+2),故无论θ为何值,AD·BC≠0,故C不正确,故选B.3.已知向量a,b满足的条件:|a|=2,|b|=,且a与2b-a互相垂直,则a与b的夹角为________.答案45...