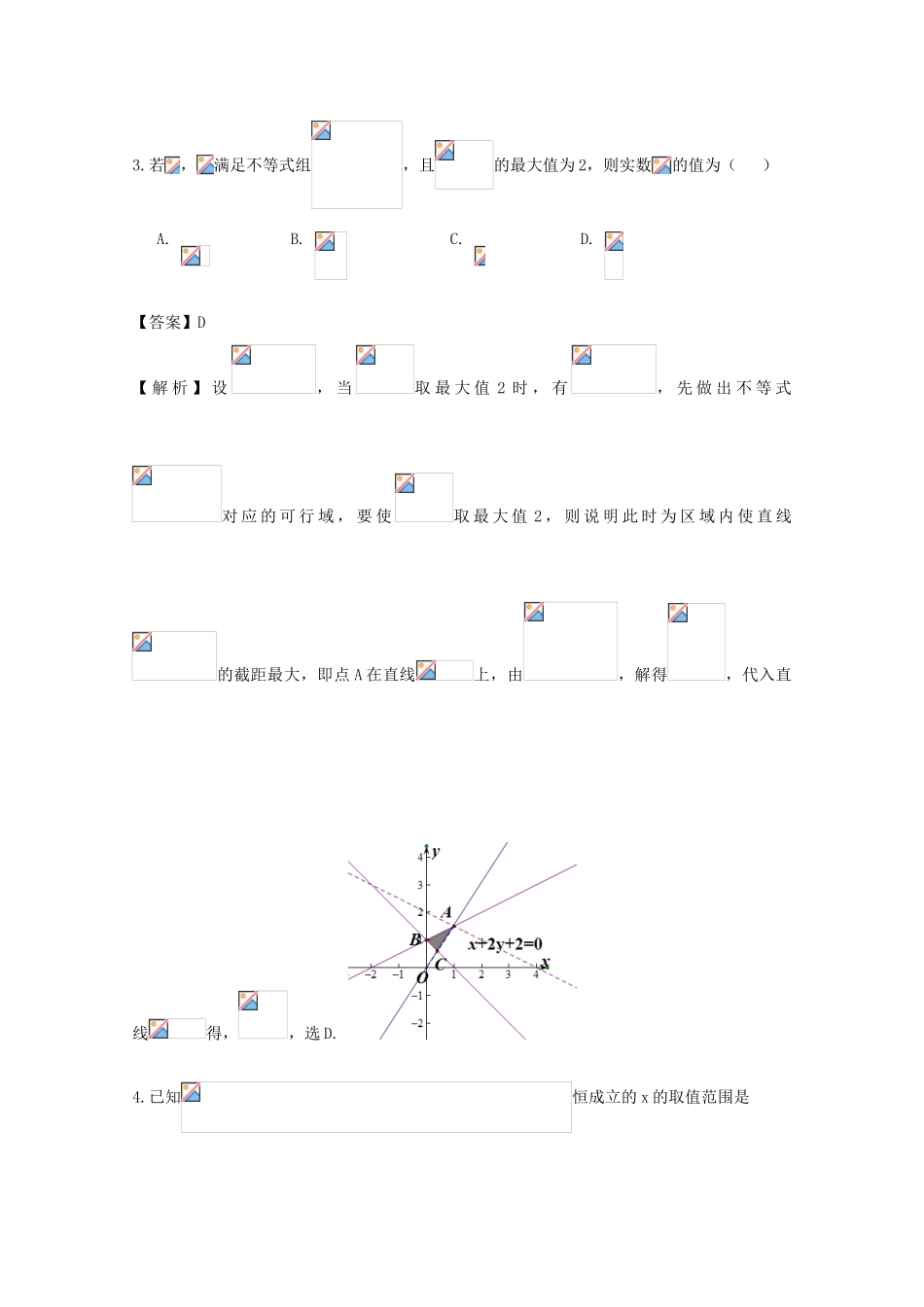
不等式011.已知,为常数,且的最大值为2,则=A.2B.4C.D.【答案】C【解析】当时,有,当且仅当时取等号。因为的最大值为2,所以,所以,选C.2.如果实数满足不等式组则的最小值是A.25B.5C.4D.1【答案】B【解析】在直角坐标系中画出不等式组所表示的平面区域如图1所示的阴影部分,x2+y2的最小值即表示阴影部分(包含边界)中的点到原点的距离的最小值的平方,由图可知直线x−y+1=0与直线x=1的交点(1,2)到原点最近,故x2+y2的最小值为12+22=5.选B.3.若,满足不等式组,且的最大值为2,则实数的值为()A.B.C.D.【答案】D【解析】设,当取最大值2时,有,先做出不等式对应的可行域,要使取最大值2,则说明此时为区域内使直线的截距最大,即点A在直线上,由,解得,代入直线得,,选D.4.已知恒成立的x的取值范围是A.B.C.D.【答案】C【解析】,所以要使不等式恒成立,则有恒成立,即,所以,因为,所以,即,所以使不等式恒成立的的取值范围是,选C.5.若直线(a>0,b>0)被圆截得的弦长为4,则的最小值为()A.B.C.D.【答案】C【解析】圆的标准方程为,所以圆心坐标为,半径为.因为直线被圆截得的弦长为4,所以线长为直径,即直线过圆心,所以,即,所以,所以,当且仅当,即,时取等号,所以的最小值为,选C.6.已知实数满足则的最小值是()A.7B.-5C.4D.-7【答案】B【解析】由得,,做直线,平移直线,由图象可知当直线经过点B时,直线的截距最大,此时最小,由得,,代入得最小值,所以选B.7.设x,y满足约束条件,若目标函数(a.>0,b>0),最大值为12,则的最小值为A.B.C.5D.4【答案】B【解析】做出可行域,由得,因为,所以直线斜率,直线截距越大,越大,做出直线,,由图象可知当直线经过点B时,截距做大,此时,由得,代入直线得,即。所以,当且仅当,即时取等号,所以选B.8.已知,满足不等式组当时,目标函数的最大值的变化范围是(A)(B)(C)(D)【答案】D【解析】,当时,对应的平面区域为阴影部分,由得,平移直线由图象可知当直线经过点C时,直线的截距最大,此时解得,即,代入得。当时,对应的平面区域为阴影部分ODE,由得,平移直线由图象可知当直线经过点E时,直线的截距最大,此时解得,即,代入得。所以目标函数的最大值的变化范围是,即,选D.9.若,则下列各式正确的是A.B.C.D.【答案】C【解析幂函数在时,单调递减,所以A错误。在定义域上不单调,错误。对数函数在定义域上单调递增,所以C正确。指数函数在定义域上单调递减,不正确。所以选C.