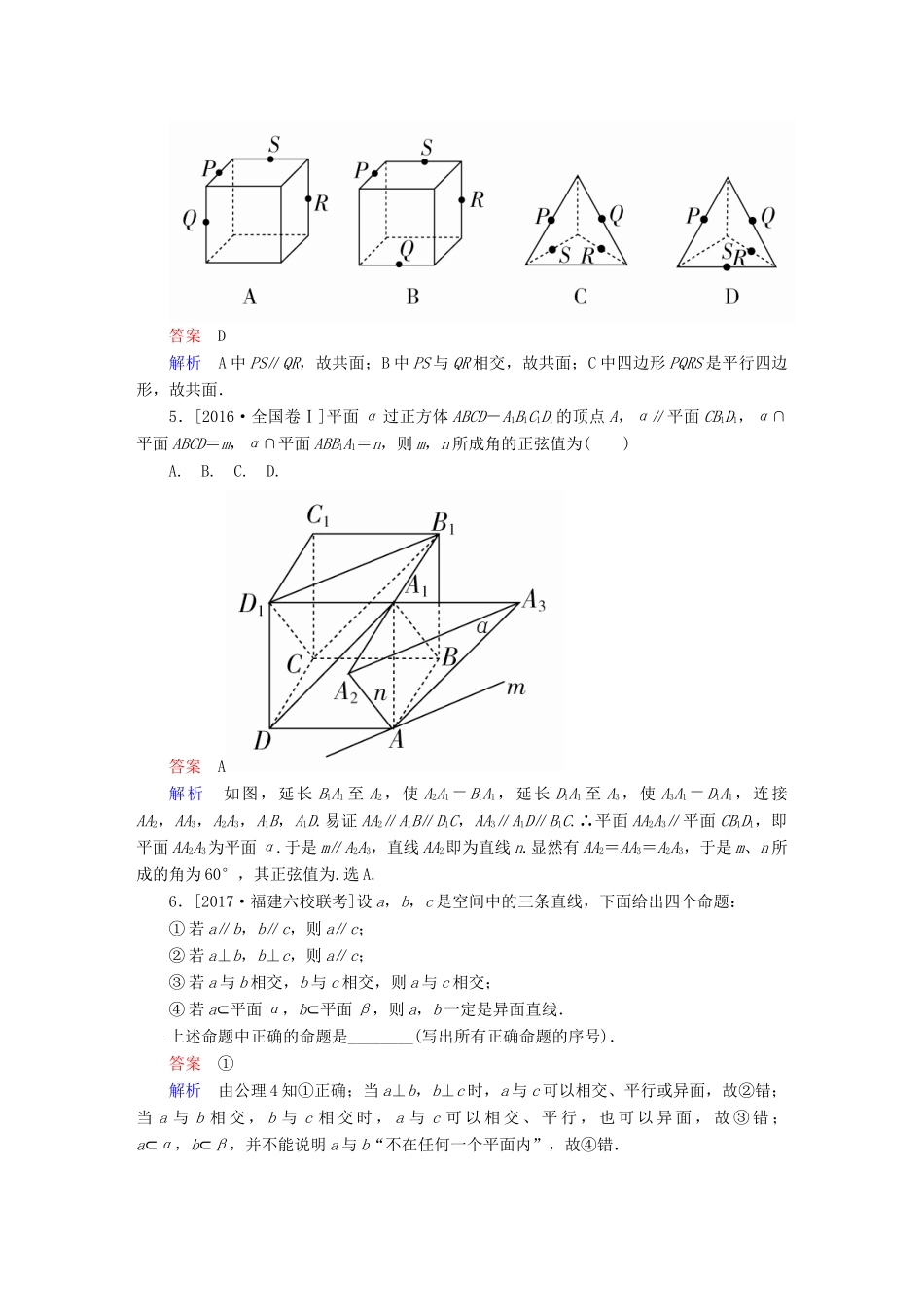
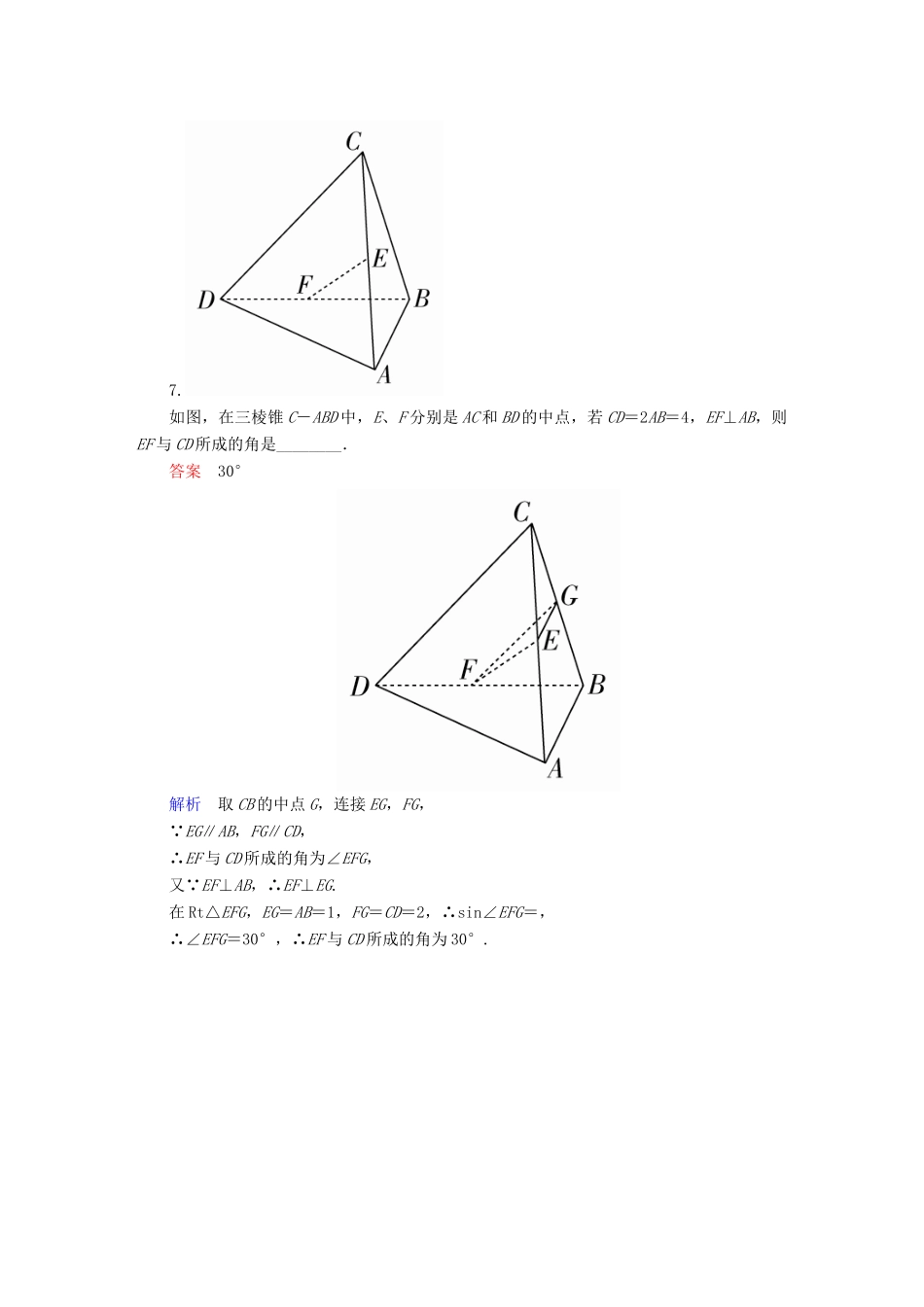
2018版高考数学一轮总复习第7章立体几何7.3空间点、直线、平面之间的位置关系模拟演练理[A级基础达标](时间:40分钟)1.[2017·福州质检]已知命题p:a,b为异面直线,命题q:直线a,b不相交,则p是q的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案A解析若直线a,b不相交,则a,b平行或异面,所以p是q的充分不必要条件,故选A.2.设A,B,C,D是空间四个不同的点,在下列命题中,不正确的是()A.若AC与BD共面,则AD与BC共面B.若AC与BD是异面直线,则AD与BC是异面直线C.若AB=AC,DB=DC,则AD⊥BCD.若AB=AC,DB=DC,则AD=BC答案D解析ABCD可能为平面四边形,也可能为空间四边形,故D不成立.3.[2017·泉州模拟]设a,b是互不垂直的两条异面直线,则下列命题成立的是()A.存在唯一直线l,使得l⊥a,且l⊥bB.存在唯一直线l,使得l∥a,且l⊥bC.存在唯一平面α,使得a⊂α,且b∥αD.存在唯一平面α,使得a⊂α,且b⊥α答案C解析a,b是互不垂直的两条异面直线,把它放入正方体中如图,由图可知A不正确由l∥a,且l⊥b,可得a⊥b,与题设矛盾,故B不正确;由a⊂α,且b⊥α,可得a⊥b,与题设矛盾,故D不正确,故选C.4.[2017·温州模拟]如图所示的是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点不共面的是()答案D解析A中PS∥QR,故共面;B中PS与QR相交,故共面;C中四边形PQRS是平行四边形,故共面.5.[2016·全国卷Ⅰ]平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为()A.B.C.D.答案A解析如图,延长B1A1至A2,使A2A1=B1A1,延长D1A1至A3,使A3A1=D1A1,连接AA2,AA3,A2A3,A1B,A1D.易证AA2∥A1B∥D1C,AA3∥A1D∥B1C.∴平面AA2A3∥平面CB1D1,即平面AA2A3为平面α.于是m∥A2A3,直线AA2即为直线n.显然有AA2=AA3=A2A3,于是m、n所成的角为60°,其正弦值为.选A.6.[2017·福建六校联考]设a,b,c是空间中的三条直线,下面给出四个命题:①若a∥b,b∥c,则a∥c;②若a⊥b,b⊥c,则a∥c;③若a与b相交,b与c相交,则a与c相交;④若a⊂平面α,b⊂平面β,则a,b一定是异面直线.上述命题中正确的命题是________(写出所有正确命题的序号).答案①解析由公理4知①正确;当a⊥b,b⊥c时,a与c可以相交、平行或异面,故②错;当a与b相交,b与c相交时,a与c可以相交、平行,也可以异面,故③错;a⊂α,b⊂β,并不能说明a与b“不在任何一个平面内”,故④错.7.如图,在三棱锥C-ABD中,E、F分别是AC和BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成的角是________.答案30°解析取CB的中点G,连接EG,FG, EG∥AB,FG∥CD,∴EF与CD所成的角为∠EFG,又 EF⊥AB,∴EF⊥EG.在Rt△EFG,EG=AB=1,FG=CD=2,∴sin∠EFG=,∴∠EFG=30°,∴EF与CD所成的角为30°.8.如图所示,是正方体的平面展开图,在这个正方体中,①BM与ED平行;②CN与BE是异面直线;③CN与BM成60°角;④DM与BN垂直.以上四个命题中,正确命题的序号是________.答案③④解析如图所示,把正方体的平面展开图还原成原来的正方体,显然BM与ED为异面直线,故命题①不成立;而CN与BE平行,故命题②不成立. BE∥CN,∴CN与BM所成角为∠MBE. ∠MBE=60°,故③正确; BC⊥面CDNM,∴BC⊥DM,又 DM⊥NC,∴DM⊥面BCN,∴DM⊥BN,故④正确,故填③④.9.如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点.已知∠BAC=,AB=2,AC=2,PA=2.求:(1)三棱锥P-ABC的体积;(2)异面直线BC与AD所成角的余弦值.解(1)S△ABC=×2×2=2,三棱锥P-ABC的体积为V=S△ABC·PA=×2×2=.(2)如图,取PB的中点E,连接DE,AE,则ED∥BC,所以∠ADE(或其补角)是异面直线BC与AD所成的角.在△ADE中,DE=2,AE=,AD=2,cos∠ADE==.故异面直线BC与AD所成角的余弦值为.10.如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.求证:(1)E、C、D1、F四点共面;(2)CE、D1F、DA三线共点.证明(1)如图所示,连接CD1、EF、A1B, E、F分别是AB和AA1的中点,∴FE∥A1B且EF=A1B. A1D1綊BC...