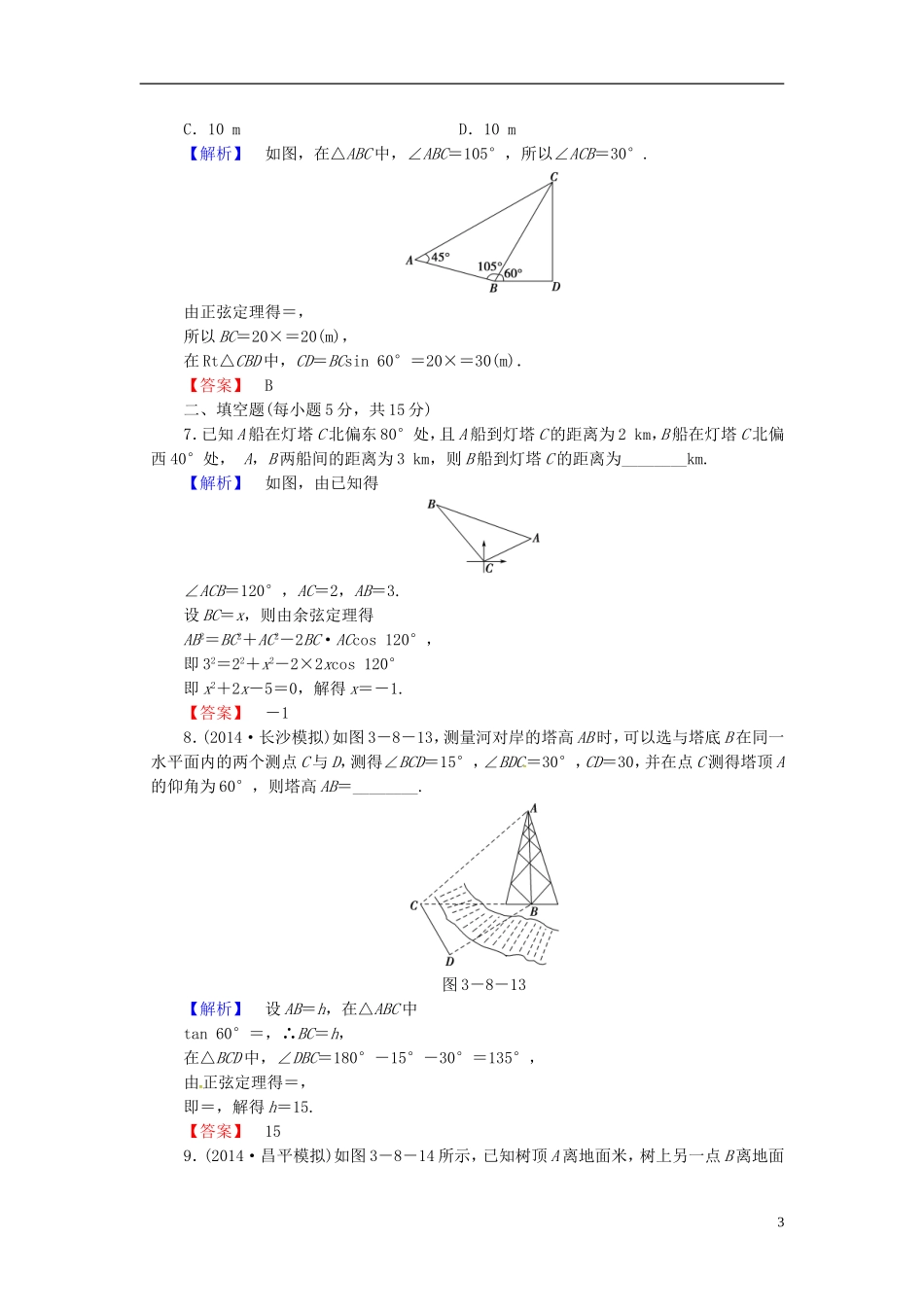
课时限时检测(二十四)正弦定理、余弦定理的应用举例(时间:60分钟满分:80分)命题报告考查知识点及角度题号及难度基础中档稍难测量距离问题1,4,710测量高度问题2,86测量角度问题59综合应用311,12一、选择题(每小题5分,共30分)1.已知A、B两地的距离为10km,B、C两地的距离为20km,现测得∠ABC=120°,则A,C两地的距离为()A.10kmB.10kmC.10kmD.10km【解析】由余弦定理得AC2=AB2+BC2-2AB·BC·cos∠ABC=100+400-2×10×20×=700,∴AC=10.【答案】D2.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为()图3-8-9A.10mB.20mC.20mD.40m【解析】设电视塔的高度为xm,则BC=x,BD=x.在△BCD中,根据余弦定理得3x2=x2+402-2×40x×cos120°,即x2-20x-800=0,解得x=-20(舍去)或x=40.故电视塔的高度为40m.【答案】D3.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时()A.5海里B.5海里C.10海里D.10海里【解析】如图,依题意有∠BAC=60°,∠BAD=75°,所以∠CAD=∠CDA=15°,从而CD=CA=10,在直角三角形ABC中,得AB=5,于是这艘船的速度是=10(海里/小时).1【答案】C4.一艘海轮从A处出发,以每小时40海里的速度沿东偏南50°方向直线航行,30分钟后到达B处.在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,那么B、C两点间的距离是()图3-8-10A.10海里B.10海里C.20海里D.20海里【解析】由已知可得,∠BAC=30°,∠ABC=105°,AB=20,从而∠ACB=45°.在△ABC中,由正弦定理,得BC=×sin30°=10.【答案】A5.(2014·南昌模拟)如图3-8-11所示,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°相距10海里C处的乙船,乙船立即朝北偏东θ+30°角的方向沿直线前往B处营救,则sinθ的值为()图3-8-11A.B.C.D.【解析】连接BC.在△ABC中,AC=10,AB=20,∠BAC=120°,由余弦定理,得BC2=AC2+AB2-2AB·AC·cos120°=700,∴BC=10,再由正弦定理,得=,∴sinθ=.【答案】A6.某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图3-8-12所示),则旗杆的高度为()图3-8-12A.10mB.30m2C.10mD.10m【解析】如图,在△ABC中,∠ABC=105°,所以∠ACB=30°.由正弦定理得=,所以BC=20×=20(m),在Rt△CBD中,CD=BCsin60°=20×=30(m).【答案】B二、填空题(每小题5分,共15分)7.已知A船在灯塔C北偏东80°处,且A船到灯塔C的距离为2km,B船在灯塔C北偏西40°处,A,B两船间的距离为3km,则B船到灯塔C的距离为________km.【解析】如图,由已知得∠ACB=120°,AC=2,AB=3.设BC=x,则由余弦定理得AB2=BC2+AC2-2BC·ACcos120°,即32=22+x2-2×2xcos120°即x2+2x-5=0,解得x=-1.【答案】-18.(2014·长沙模拟)如图3-8-13,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30,并在点C测得塔顶A的仰角为60°,则塔高AB=________.图3-8-13【解析】设AB=h,在△ABC中tan60°=,∴BC=h,在△BCD中,∠DBC=180°-15°-30°=135°,由正弦定理得=,即=,解得h=15.【答案】159.(2014·昌平模拟)如图3-8-14所示,已知树顶A离地面米,树上另一点B离地面3米,某人在离地面米的C处看此树,则该人离此树________米时,看A,B的视角最大.图3-8-14【解析】过C作CF⊥AB于点F,设∠ACB=α,∠BCF=β.由已知得AB=-=5(米),BF=-=4(米),AF=-=9(米).则tan(α+β)==,tanβ==,∴tanα=[(α+β)-β]===≤=.当且仅当FC=,即FC=6时,tanα取得最大值,...