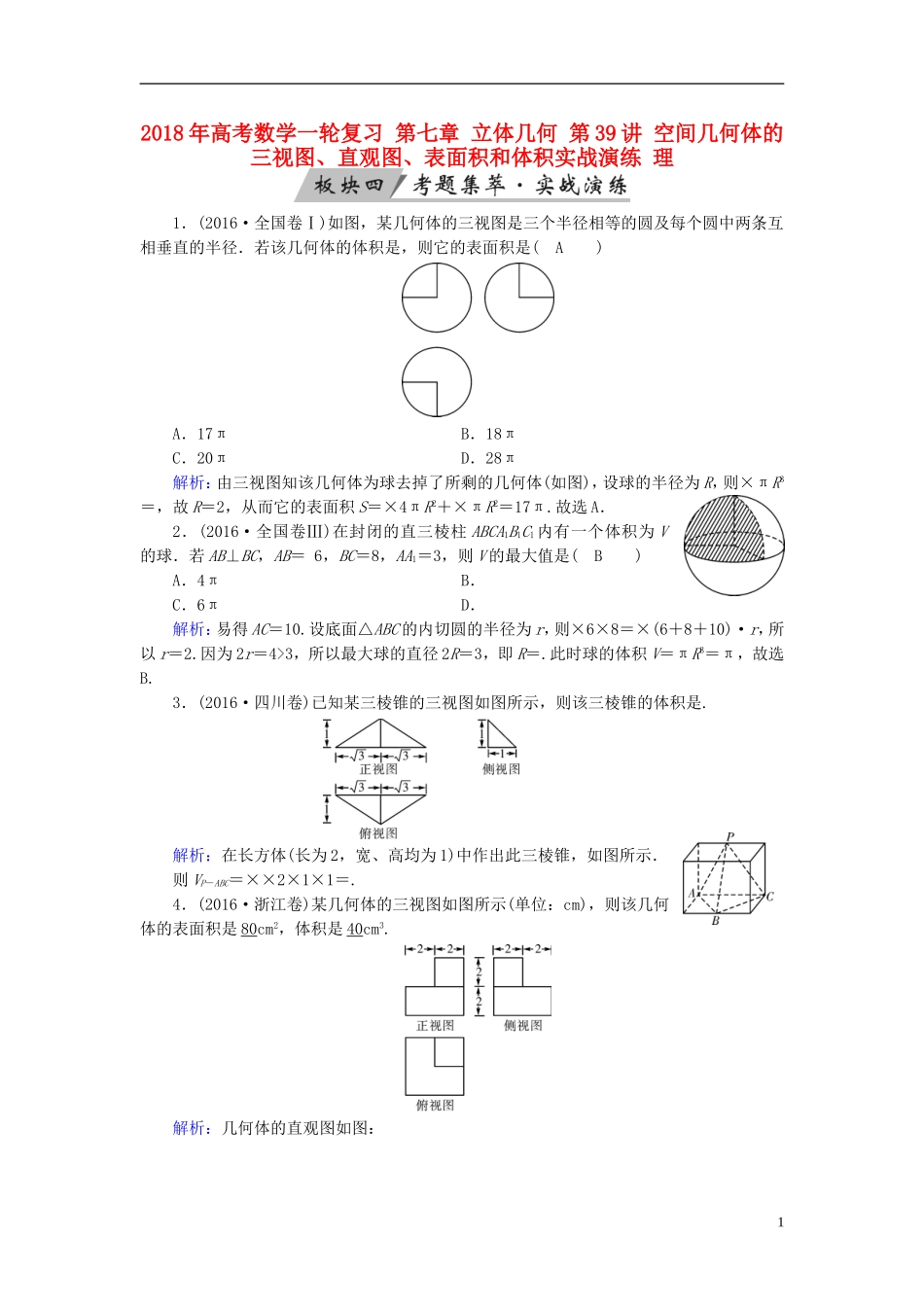
2018年高考数学一轮复习第七章立体几何第39讲空间几何体的三视图、直观图、表面积和体积实战演练理1.(2016·全国卷Ⅰ)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是(A)A.17πB.18πC.20πD.28π解析:由三视图知该几何体为球去掉了所剩的几何体(如图),设球的半径为R,则×πR3=,故R=2,从而它的表面积S=×4πR2+×πR2=17π.故选A.2.(2016·全国卷Ⅲ)在封闭的直三棱柱ABCA1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是(B)A.4πB.C.6πD.解析:易得AC=10.设底面△ABC的内切圆的半径为r,则×6×8=×(6+8+10)·r,所以r=2.因为2r=4>3,所以最大球的直径2R=3,即R=.此时球的体积V=πR3=π,故选B.3.(2016·四川卷)已知某三棱锥的三视图如图所示,则该三棱锥的体积是.解析:在长方体(长为2,宽、高均为1)中作出此三棱锥,如图所示.则VP-ABC=××2×1×1=.4.(2016·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的表面积是80cm2,体积是40cm3.解析:几何体的直观图如图:1则S表=42×2+4×2×4+22×4=80(cm2),V=23+4×4×2=40(cm3).2