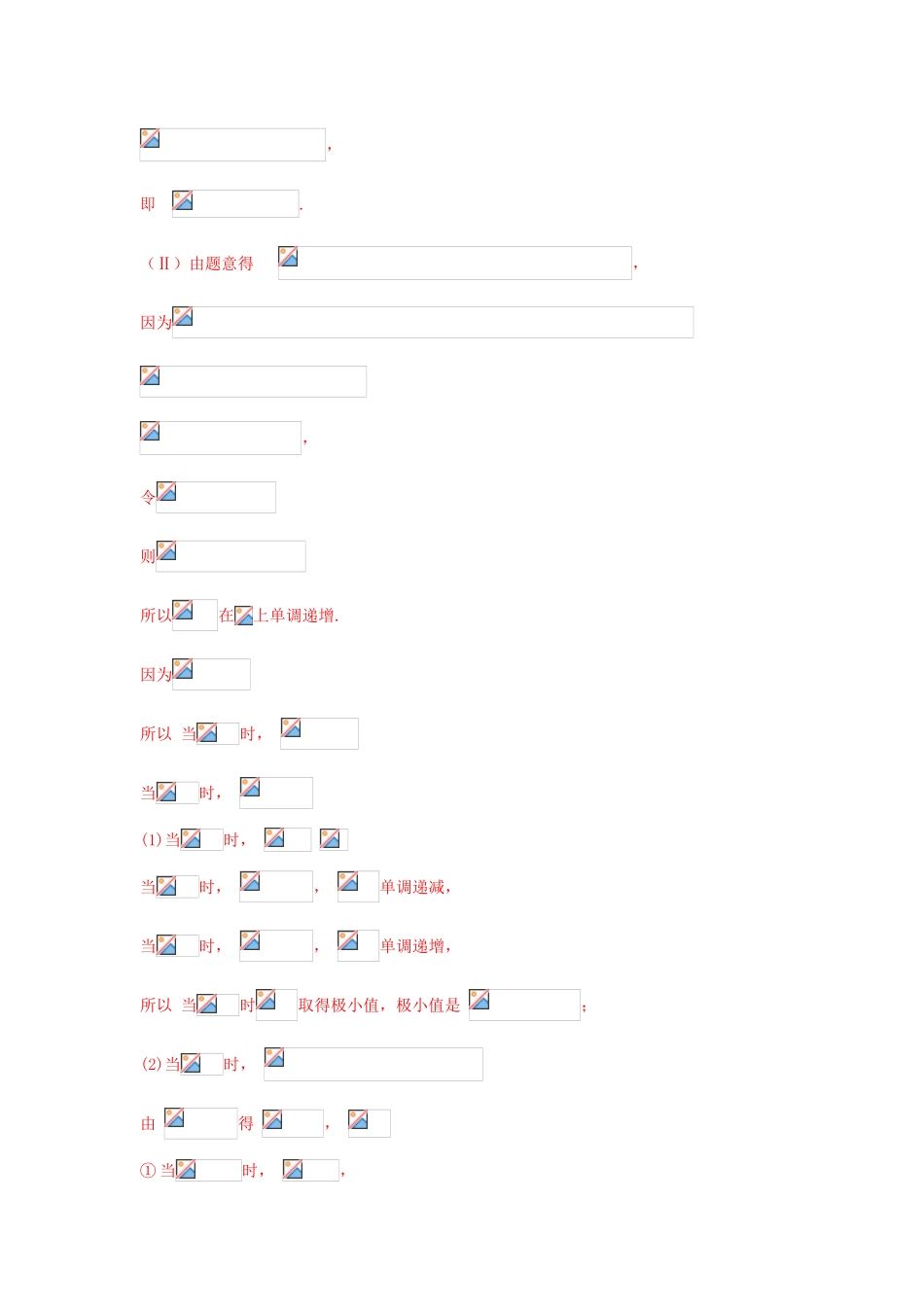
专题10导数的概念及运算1.了解导数概念的实际背景。2.通过函数图象直观理解导数的几何意义。3.能根据导数的定义求函数y=c(c为常数),y=x,y=,y=x2,y=x3,y=的导数。4.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数。热点题型一导数的计算例1、求下列函数的导数(1)y=exsinx;(2)y=x;(3)y=x-sincos。(4)y=ln(1-2x)。【提分秘籍】导数计算的原则和方法(1)原则:先化简解析式,使之变成能用八个求导公式求导的函数的和、差、积、商,再求导。(2)方法:①连乘积形式:先展开化为多项式的形式,再求导;②分式形式:观察函数的结构特征,先化为整式函数或较为简单的分式函数,再求导;③对数形式:先化为和、差和的形式,再求导;④根式形式:先化为分数指数幂的形式,再求导;⑤三角形式:先利用三角函数公式转化为和或差的形式,再求导。【举一反三】求下列函数的导数(1)y=(2x2-1)(3x+1);(2)y=;(3)y=-sin。解析:(1)因为y=(2x2-1)(3x+1)=6x3+2x2-3x-1,所以,y′=(6x3)′+(2x2)′-(3x)′=18x2+4x-3。(2)因为y==x+x3+,所以,y′=(x)′+(x3)′+′=-x+3x2+=3x2+x-2cosx-x-2x-3sinx。(3)因为y=-sin=sin=sincos=sinx,所以,y′=cosx。热点题型二导数的几何意义及应用例2、【2017山东,理20】已知函数,,其中是自然对数的底数.(Ⅰ)求曲线在点处的切线方程;(Ⅱ)令,讨论的单调性并判断有无极值,有极值时求出极值.【答案】(1)(2)见解析【解析】(Ⅰ)由题意又,所以,因此曲线在点处的切线方程为,即.(Ⅱ)由题意得,因为,令则所以在上单调递增.因为所以当时,当时,(1)当时,当时,,单调递减,当时,,单调递增,所以当时取得极小值,极小值是;(2)当时,由得,①当时,,当时,,单调递增;当时,,单调递减;当时,,单调递增.所以当时取得极大值.极大值为,当时取到极小值,极小值是;②当时,,所以当时,,函数在上单调递增,无极值;极小值是.综上所述:当时,在上单调递减,在上单调递增,函数有极小值,极小值是;当时,函数在和和上单调递增,在上单调递减,函数有极大值,也有极小值,极大值是极小值是;当时,函数在上单调递增,无极值;当时,函数在和上单调递增,在上单调递减,函数有极大值,也有极小值,极大值是;极小值是.【提分秘籍】导数几何意义的应用及解决(1)已知切点A(x0,y0)求斜率k,即求该点处的导数值k=f′(x0)。(2)已知斜率k,求切点A(x1,f(x1)),即解方程f′(x1)=k。(3)求过某点M(x1,y1)的切线方程时,需设出切点A(x0,f(x0)),则切线方程为y-f(x0)=f′(x0)(x-x0),再把点M(x1,y1)代入切线方程,求x0。(4)根据导数的几何意义求参数的值时,一般是利用切点P(x0,y0)既在曲线上又在切线上构造方程组求解。提醒:当切线方程中x(或y)的系数含有字母参数时,则切线恒过定点。【举一反三】设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x,则a=()A.0B.1C.2D.3解析:y′=a-,由题意得y′|x=0=2,即a-1=2,所以a=3。答案:D【2017天津,理20】设,已知定义在R上的函数在区间内有一个零点,为的导函数.(Ⅰ)求的单调区间;(Ⅱ)设,函数,求证:;(Ⅲ)求证:存在大于0的常数,使得对于任意的正整数,且满足.【答案】(Ⅰ)增区间是,,递减区间是.(Ⅱ)见解析;(III)见解析.【解析】(Ⅰ)解:由,可得,进而可得.令,解得,或.当x变化时,的变化情况如下表:x+-+↗↘↗所以,的单调递增区间是,,单调递减区间是.(III)证明:对于任意的正整数,,且,令,函数.由(II)知,当时,在区间内有零点;当时,在区间内有零点.所以在内至少有一个零点,不妨设为,则.由(I)知在上单调递增,故,于是.因为当时,,故在上单调递增,所以在区间上除外没有其他的零点,而,故.又因为,,均为整数,所以是正整数,从而.所以.所以,只要取,就有.【2017山东,理20】已知函数,,其中是自然对数的底数.(Ⅰ)求曲线在点处的切线方程;(Ⅱ)令,讨论的单调性并判断有无极值,有极值时求出极值.【答案】(1)(2)见解析【解析】(Ⅱ)由题意...