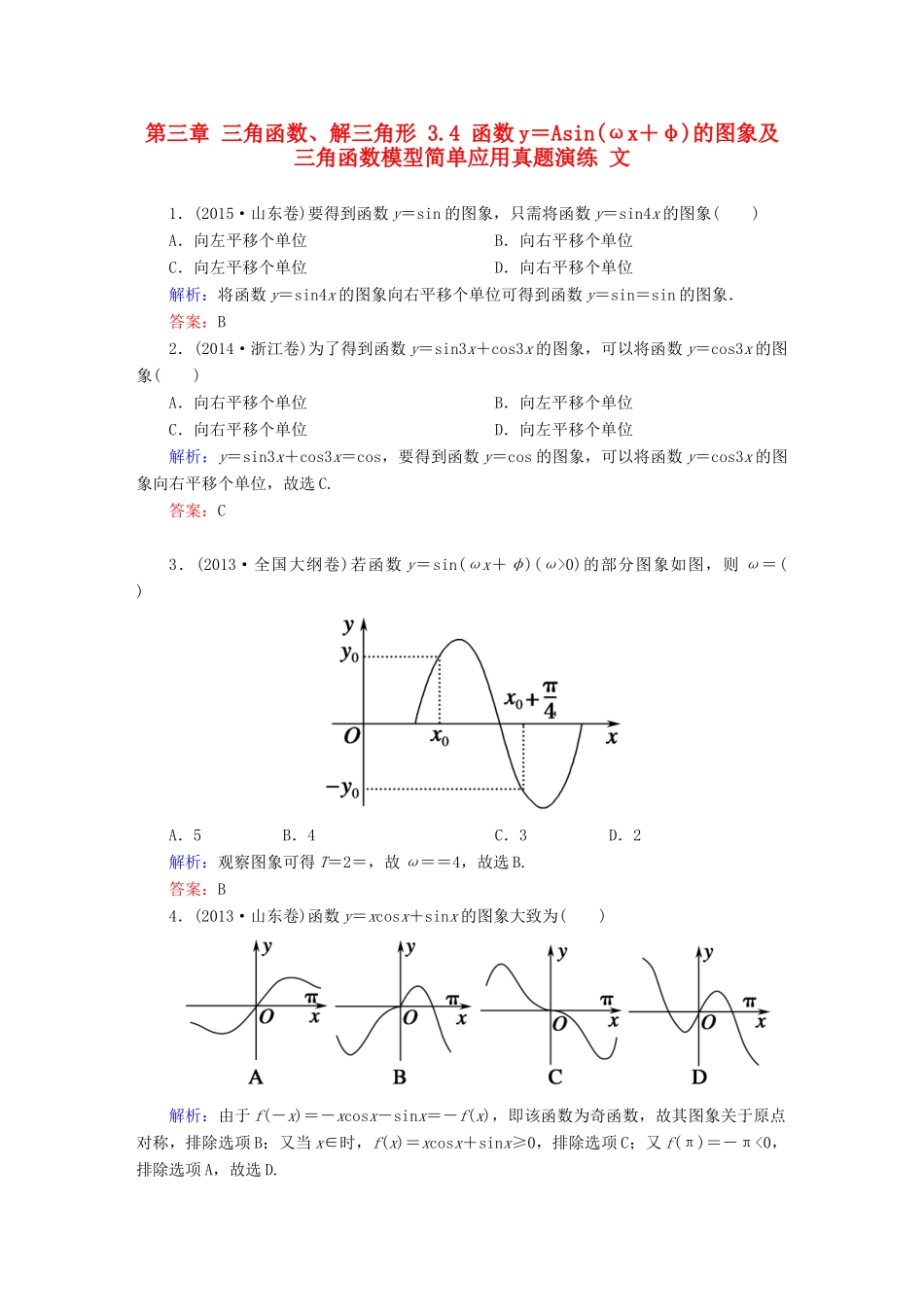
第三章三角函数、解三角形3.4函数y=Asin(ωx+φ)的图象及三角函数模型简单应用真题演练文1.(2015·山东卷)要得到函数y=sin的图象,只需将函数y=sin4x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位解析:将函数y=sin4x的图象向右平移个单位可得到函数y=sin=sin的图象.答案:B2.(2014·浙江卷)为了得到函数y=sin3x+cos3x的图象,可以将函数y=cos3x的图象()A.向右平移个单位B.向左平移个单位C.向右平移个单位D.向左平移个单位解析:y=sin3x+cos3x=cos,要得到函数y=cos的图象,可以将函数y=cos3x的图象向右平移个单位,故选C.答案:C3.(2013·全国大纲卷)若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=()A.5B.4C.3D.2解析:观察图象可得T=2=,故ω==4,故选B.答案:B4.(2013·山东卷)函数y=xcosx+sinx的图象大致为()解析:由于f(-x)=-xcosx-sinx=-f(x),即该函数为奇函数,故其图象关于原点对称,排除选项B;又当x∈时,f(x)=xcosx+sinx≥0,排除选项C;又f(π)=-π<0,排除选项A,故选D.答案:D5.(2011·辽宁卷)已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<),y=f(x)的部分图象如图,则f=()A.2+B.C.D.2-解析:本题考查正切函数的图象与性质及待定系数法,难度中等.观察图象可知其周期为2=,故=⇒ω=2,即f(x)=Atan(2x+φ),又f=Atan=0,则+φ=kπ⇒φ=kπ-(k∈Z),又|φ|<,故φ=,再由f(0)=Atan=A=1,故f(x)=tan,因此f=tan=tan=.答案:B6.(2013·福建卷)将函数f(x)=sin(2x+θ)的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P,则φ的值可以是()A.B.C.D.解析:f(x)的图象向右平移φ个单位得g(x)=sin[2(x-φ)+θ],由题意可得解得θ=.经检验φ=π符合.答案:B