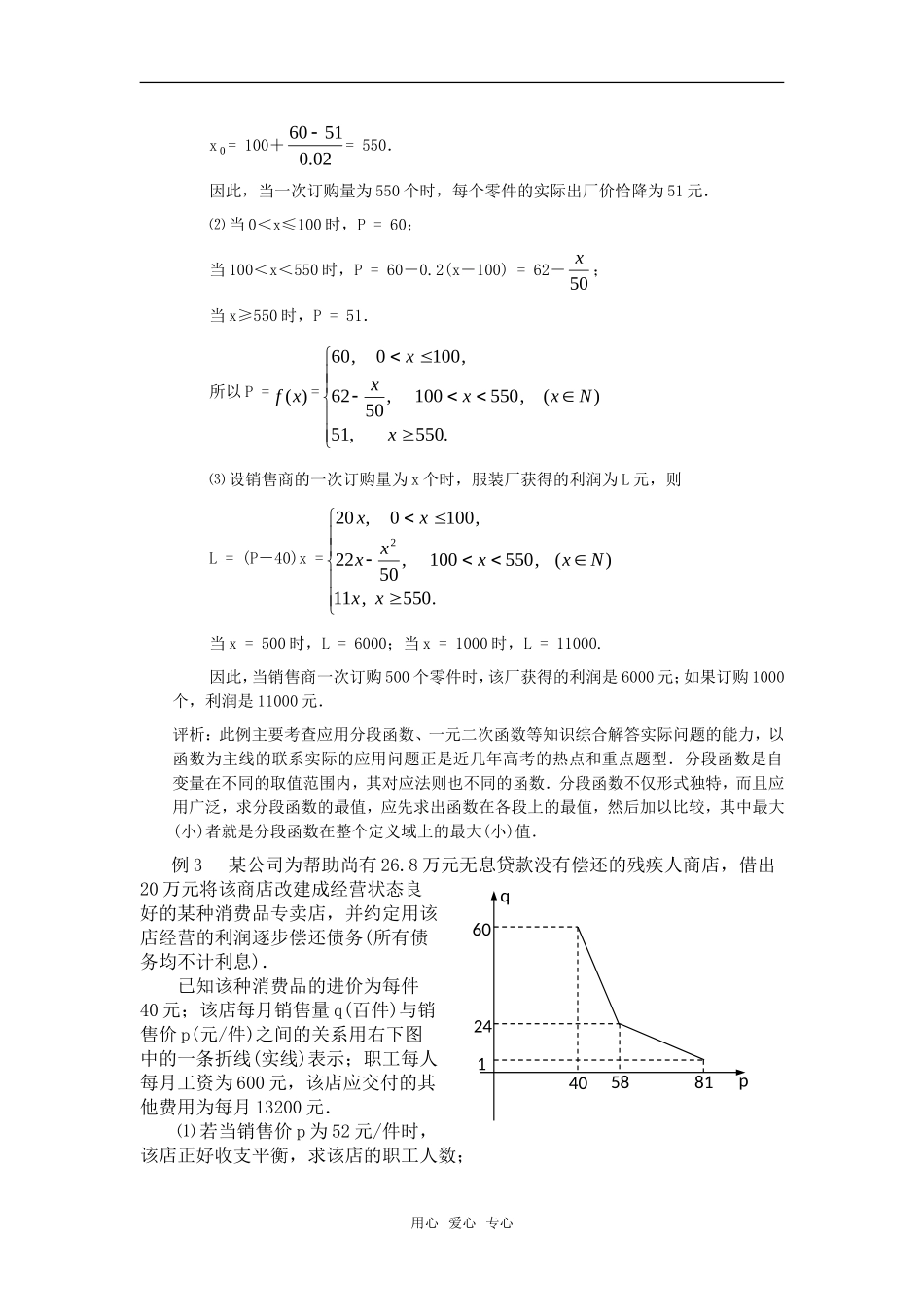
函数应用题中的最值问题选解函数是高中数学主要内容,涉及函数的应用问题,题源丰富、背景深刻、题型新颖、解法灵活,是历年高考的热点之一.有很多应用体涉及到“方案最优化”问题,其解决方法一般是建立“目标函数”,从而化归为求目标函数的最大值或最小值问题.例1渔场中鱼群的最大养殖量是m吨,为保证鱼群的生长空间,实际养殖量不能达到最大养殖量,必须留出适当的空闲量.已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比,比例系数为k(k>0).⑴写出y关于x的函数关系式,并指出这个函数的定义域;⑵求鱼群年增长量的最大值;⑶当鱼群的年增长量达到最大值时,求k的取值范围.解:⑴因鱼群的年增长量为m吨,实际养殖量为x吨,则空闲量为(m-x)吨,空闲率为mxm=1-mx.依题意,鱼群年增长量为:y=kx(1-mx),定义域为0<x<m.⑵y=kx(1-mx)=-mk(x-2m)2+4km,当x=2m时,ymax=4km,即鱼群年增长量的最大值为4km.⑶由于实际养殖量和年增长量之和小于最大养殖量,所以有0<x+y<m,即0<2m+4km<m,解得-2<k<2,再注意到k>0,得0<k<2.评析:此题中专业术语多,如最大养殖量、实际养殖量和年增长量等,很不容易理解清楚,主要问题是抓住涉及数量关系的一句话:“已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比.”理解并求出空闲率mxm,就可列出函数表达式.由于是二次函数,处理时可依据二次函数求最值的方法来求.而实际养殖量和年增长量之和小于最大养殖量应是社会常识,在阅读题意中要得到这个隐含条件.例2某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.⑴当一次订购量为多少个时,零件的实际出厂单价恰降为51元?⑵设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=)(xf的表达式;⑶当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本).解:⑴设每个零件的实际出厂价恰好降为51元,一次订购两为x0个,则用心爱心专心x0=100+02.05160=550.因此,当一次订购量为550个时,每个零件的实际出厂价恰降为51元.⑵当0<x≤100时,P=60;当100<x<550时,P=60-0.2(x-100)=62-50x;当x≥550时,P=51.所以P=)(xf=.550,51)(,550100,5062,1000,60xNxxxx⑶设销售商的一次订购量为x个时,服装厂获得的利润为L元,则L=(P-40)x=.550,11)(,550100,5022,1000,202xxNxxxxxx当x=500时,L=6000;当x=1000时,L=11000.因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润是11000元.评析:此例主要考查应用分段函数、一元二次函数等知识综合解答实际问题的能力,以函数为主线的联系实际的应用问题正是近几年高考的热点和重点题型.分段函数是自变量在不同的取值范围内,其对应法则也不同的函数.分段函数不仅形式独特,而且应用广泛,求分段函数的最值,应先求出函数在各段上的最值,然后加以比较,其中最大(小)者就是分段函数在整个定义域上的最大(小)值.例3某公司为帮助尚有26.8万元无息贷款没有偿还的残疾人商店,借出20万元将该商店改建成经营状态良好的某种消费品专卖店,并约定用该店经营的利润逐步偿还债务(所有债务均不计利息).已知该种消费品的进价为每件40元;该店每月销售量q(百件)与销售价p(元/件)之间的关系用右下图中的一条折线(实线)表示;职工每人每月工资为600元,该店应交付的其他费用为每月13200元.⑴若当销售价p为52元/件时,该店正好收支平衡,求该店的职工人数;用心爱心专心pq16024405881⑵若该店只安排40名职工,则该店最早可在几年后还清所有债务,此时每件消费品的价格定为多少元?解:⑴设该店的月利润为S元,有职工m名.则S=q(p-40)×100-600m-13200.又由图可知:q=2140,(4058)82.(5881)pppp所以,S=(2140)(40)10060013200,(4058)(80)(40)1006001320...