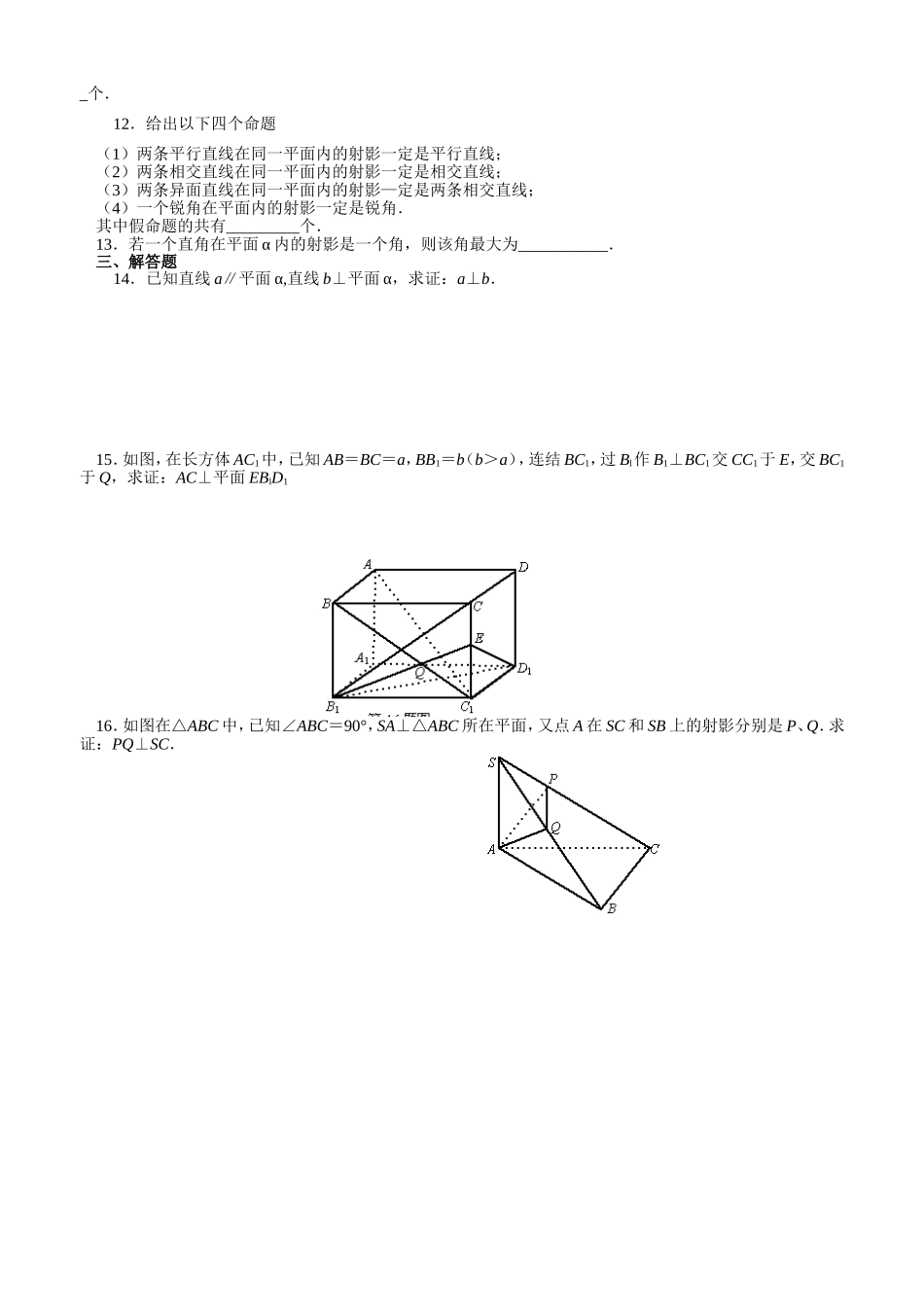
直线与平面垂直的判定与性质一、选择题1.两异面直线在平面α内的射影()A.相交直线B.平行直线C.一条直线—个点D.以上三种情况均有可能2.若两直线a与b异面,则过a且与b垂直的平面()A.有且只有—个B.可能存在也可能不存在C.有无数多个D.—定不存在3.在空间,下列哪些命题是正确的()①平行于同一条直线的两条直线互相平行;②垂直于同一条直线的两条直线互相平行;③平行于同一个平面的两条直线互相平行;④垂直于同—个平面的两条直线互相平行.A.仅②不正确B.仅①、④正确C.仅①正确D.四个命题都正确4.若平面α的斜线l在α上的射影为l′,直线b∥α,且b⊥l′,则b与l()A.必相交B.必为异面直线C.垂直D.无法确定5.下列命题①平面的每条斜线都垂直于这个平面内的无数条直线;②若一条直线垂直于平面的斜线,则此直线必垂直于斜线在此平面内的射影;③若平面的两条斜线段相等,则它们在同一平面内的射影也相等;④若一条线段在平面外并且不垂直于这个平面,则它的射影长一定小于线段的长.其中,正确的命题有()A.1个B.2个C.3个n4个6.在下列四个命题中,假命题为()A.如果一条直线垂直于平面内的无数条直线,那么这条直线和这个平面垂直B.垂直于三角形两边的直线必垂直于第三边C.过点A垂直于直线a的所有直线都在过点A垂直于a的平面内D.如果三条共点直线两两垂直,那么其中一条直线垂直于另两条直线确定的平面7.已知P是四边形ABCD所在平面外一点且P在平面ABCD内的射影在四边形ABCD内,若P到这四边形各边的距离相等,那么这个四边形是()A.圆内接四边形B.矩形C.圆外切四边形D.平行四边形8.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离等于()A.5B.52C.35D.45二、填空题9.AB是平面α的斜线段,其长为a,它在平面α内的射影A′B的长为b,则垂线A′A_________.10.如果直线l、m与平面α、β、γ满足:l=β∩γ,l⊥α,mÌα和m⊥γ,现给出以下四个结论:①α∥γ且l⊥m;②αγ且m∥β③αβ且l⊥m;④αγ且l⊥m;其中正确的为“________”.(写出序号即可)11.如图,正方形ABCD,P是正方形平面外的一点,且PA⊥平面ABCD则在△PAB、△PBC、△PCD、△PAD、△PAC及△PBD中,为直角三角形有_________个.12.给出以下四个命题(1)两条平行直线在同一平面内的射影一定是平行直线;(2)两条相交直线在同一平面内的射影一定是相交直线;(3)两条异面直线在同一平面内的射影—定是两条相交直线;(4)一个锐角在平面内的射影一定是锐角.其中假命题的共有_________个.13.若一个直角在平面α内的射影是一个角,则该角最大为___________.三、解答题14.已知直线a∥平面α,直线b⊥平面α,求证:a⊥b.15.如图,在长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过Bl作B1⊥BC1交CC1于E,交BC1于Q,求证:AC⊥平面EBlD116.如图在△ABC中,已知∠ABC=90°,SA⊥△ABC所在平面,又点A在SC和SB上的射影分别是P、Q.求证:PQ⊥SC.