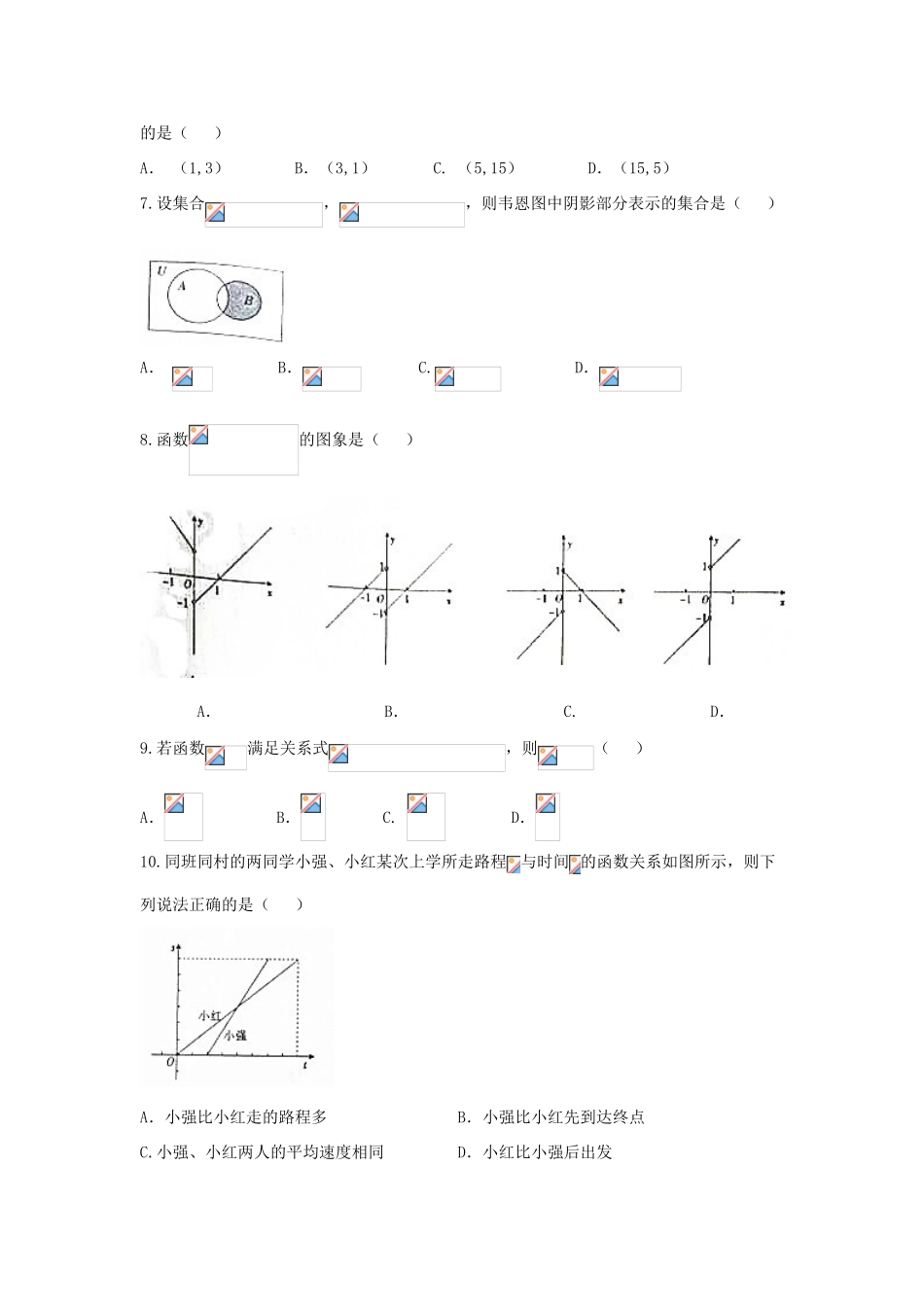
张家口市2017年度第一学期阶段测试卷高一数学试卷第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,,则()A.B.C.D.2.已知函数,则()A.2B.-2C.1D.-13.下列各选项中,不能组成集合的是()A.所有的整数B.所有大于0的数C.班上所有长得帅的同学D.所有的偶数4.下列四组函数中,与表示同一函数的是()A.,B.,C.,D.,5.下列四个函数中,在上为减函数的是()A.B.C.D.6.若点在映射下对应的点是,则在映射下对应的点为(5,5)的是()A.(1,3)B.(3,1)C.(5,15)D.(15,5)7.设集合,,则韦恩图中阴影部分表示的集合是()A.B.C.D.8.函数的图象是()A.B.C.D.9.若函数满足关系式,则()A.B.C.D.10.同班同村的两同学小强、小红某次上学所走路程与时间的函数关系如图所示,则下列说法正确的是()A.小强比小红走的路程多B.小强比小红先到达终点C.小强、小红两人的平均速度相同D.小红比小强后出发11.定义集合运算:,设,,则集合的真子集个数为()A.8B.7C.16D.1512.设函数是定义在上的增函数,则实数的取值范围是()A.B.C.D.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.函数的定义域为.14.已知两个函数和的定义域和值域都是集合,其定义如下表:则.15.设,集合,则.16.某班进行集体活动,为活跃气氛,班主任要求班上60名同学从唱歌、跳舞、讲故事三个节目中至少选择一个节目为大家表演,已知报名参加唱歌、跳舞、讲故事的人数分别为40,20,30,同时参加唱歌和讲故事的有15人,同时参加唱歌和跳舞的有10人,则同时只参加跳舞和讲故事的人数为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设全集,集合,,.(1)求,,;(2)求.18.(1)已知,求的解析式;(2)已知是一次函数,且满足,求的解析式.19.已知集合,,若,求实数的取值范围.20.已知函数.(1)判断函数在上的单调性,并用定义法加以证明;(2)求在上的最大值.21.已知函数.(1)求函数的定义域;(2)求函数的值域.22.若是定义在上的增函数,且对任意,满足,已知.(1)解不等式;(2)若,求的解析式,并在如图所示的平面直角坐标系中画出函数在区间上的图象.张家口市2017年度第一学期阶段测试卷高一数学试卷参考答案一、选择题1-5:BACDA6-10:BCBAB11、12:BD二、填空题13.14.215.-216.5三、解答题17.解:(1),,.(2).18.解:(1)令,则,所以,即函数.(2)设,则由,得,即,所以,解得.所以.19.解:.(1)当时,由,得.(2)当时,则,即.所以实数的取值范围是.20.解:(1)设是区间上的任意两个实数,且,则.由,得,,,于是,即.所以函数是区间上的减函数.(2)∵在上单调递减,也在上单调递减,∴在上单调递减,∴.21.解:(1)由,得.所以函数的定义域为.(2)令,则,原函数值域等价于函数的值域,结合二次函数图象可知,.22.解:(1)∵,∴,∵,∴,∴等价于,又是定义在上的增函数,∴,得.∴原不等式的解集为.(2)∵,∴,∴,∵,∴,又在上递增,∴.结合函数性质可知,在区间上单调递增,函数在区间上的图象如图所示: