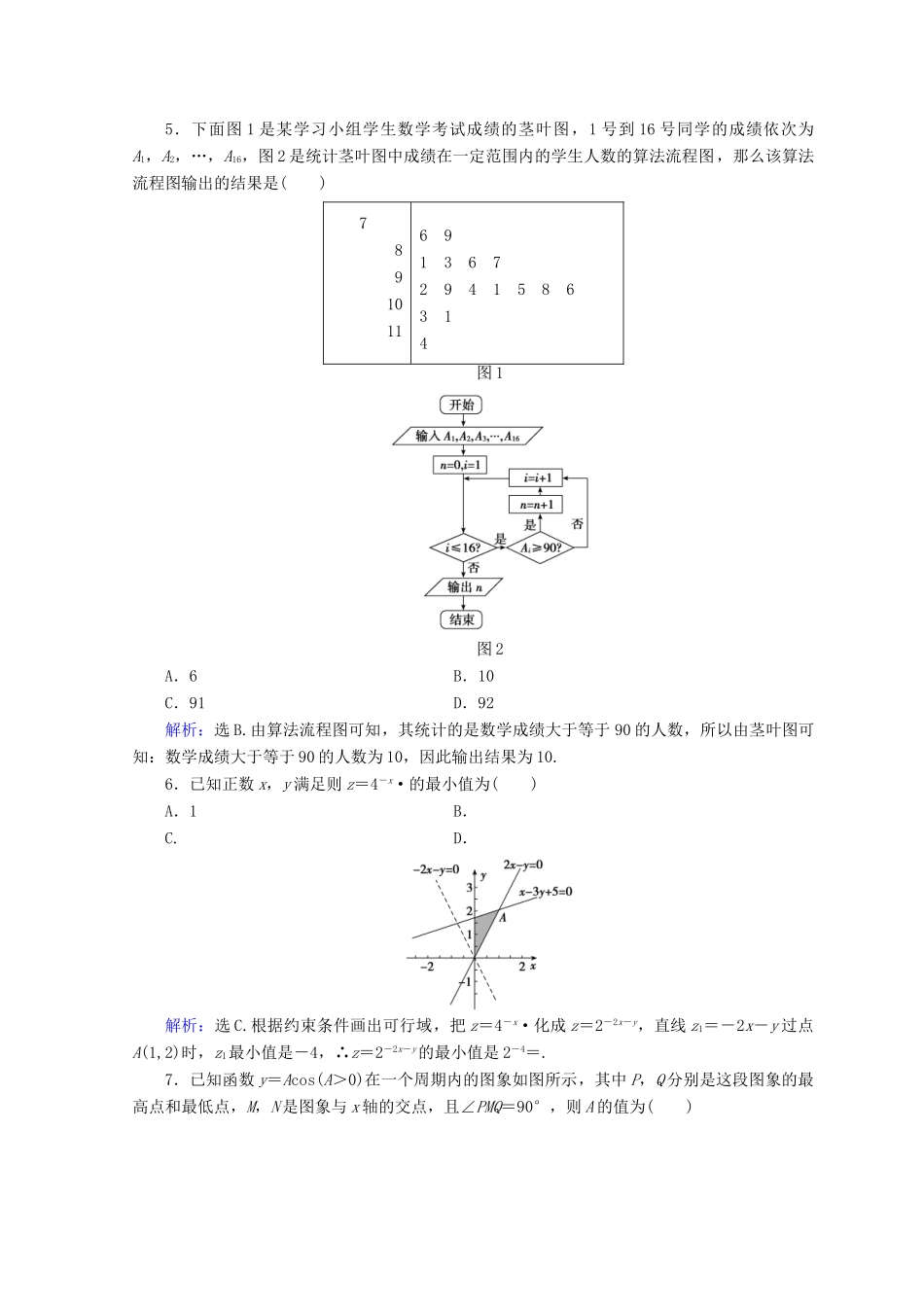
小题提速练(七)(满分80分,押题冲刺,45分钟拿下客观题满分)一、选择题(本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U=R,A={x∈N|2x(x-4)<1},B={x∈N|y=ln(2-x)},则图中阴影部分表示的集合的子集个数为()A.1B.2C.3D.4解析:选D.由韦恩图知阴影部分表示的是A∩(∁UB), A={x∈N|2x(x-4)<1}={1,2,3},B={x∈N|y=ln(2-x)}={0,1},∴阴影部分对应的集合是A∩(∁UB)={2,3},则图中阴影部分表示的集合的子集个数为22=4.2.若复数(a∈R,i为虚数单位)是纯虚数,则实数a的值为()A.-6B.-2C.4D.6解析:选A. ==为纯虚数,∴解得a=-6.3.给出命题p:若平面α与平面β不重合,且平面α内有不共线的三点到平面β的距离相等,则α∥β;命题q:向量a=(-2,-1),b=(λ,1)的夹角为钝角的充要条件为λ∈.关于以上两个命题,下列结论中正确的是()A.命题“p∨q”为假B.命题“p∧q”为真C.命题“p∨﹁q”为假D.命题“p∧﹁q”为真解析:选A.命题p:若平面α与平面β不重合,且平面α内有不共线的三点到平面β的距离相等,则α∥β或相交,因此是假命题;命题q:向量a=(-2,-1),b=(λ,1)的夹角为钝角的充要条件为-2λ-1<0,解得λ>-,由-λ+2=0,解得λ=2,此时a与b异向共线,因此向量a=(-2,-1),b=(λ,1)的夹角为钝角的充要条件为λ∈且λ≠2,因此是假命题.4.一个空间几何体的三视图如图所示,则该几何体的外接球的表面积为()A.24πB.6πC.4πD.2π解析:选B.几何体为三棱锥,可以将其补形为一个棱长为的正方体,该正方体的外接球和几何体的外接球为同一个,故2R=,R=,所以外接球的表面积为4πR2=6π.5.下面图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为A1,A2,…,A16,图2是统计茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是()78910116913672941586314图1图2A.6B.10C.91D.92解析:选B.由算法流程图可知,其统计的是数学成绩大于等于90的人数,所以由茎叶图可知:数学成绩大于等于90的人数为10,因此输出结果为10.6.已知正数x,y满足则z=4-x·的最小值为()A.1B.C.D.解析:选C.根据约束条件画出可行域,把z=4-x·化成z=2-2x-y,直线z1=-2x-y过点A(1,2)时,z1最小值是-4,∴z=2-2x-y的最小值是2-4=.7.已知函数y=Acos(A>0)在一个周期内的图象如图所示,其中P,Q分别是这段图象的最高点和最低点,M,N是图象与x轴的交点,且∠PMQ=90°,则A的值为()A.B.C.1D.2解析:选A.过Q,P分别作x轴的垂线于B,C, 函数的周期T==4,∴MN=2,CN=1, ∠PMQ=90°,∴PQ=2MN=4,即PN=2,即PC===,∴A=.8.已知函数f(n)=n2cos(nπ),且an=f(n)+f(n+1),则a1+a2+a3+…+a100=()A.0B.-100C.100D.10200解析:选B.由题意可得an=n2cos(nπ)+(n+1)2cos[(n+1)π]=(-1)n-1(2n+1),所以a1+a2+a3+…+a100=3-5+7-9+11-…+199-201=50×(-2)=-100.9.函数f(x)是定义域为R的奇函数,且x≤0时,f(x)=2x-x+a,则函数f(x)的零点个数是()A.1B.2C.3D.4解析:选C. 函数f(x)是定义域为R的奇函数,∴f(0)=0,又 x≤0时,f(x)=2x-x+a,∴f(0)=20+a=0,解得a=-1,故x≤0时,f(x)=2x-x-1,令f(x)=2x-x-1=0,解得x=-1或x=0,故f(-1)=0,则f(1)=0,综上所述,函数f(x)的零点个数是3个.10.设A1,A2分别为双曲线C:-=1(a>0,b>0)的左右顶点,若双曲线上存在点M使得两直线斜率kMA1·kMA2<2,则双曲线C的离心率的取值范围为()A.(0,)B.(1,)C.(,+∞)D.(0,3)解析:选B.由题意可得A1(-a,0),A2(a,0),设M(m,n),可得-=1,即=,由题意kMA1·kMA2<2,即为·<2,即有<2,即b2<2a2,c2-a2<2a2,即c2<3a2,c<a,即有e=<,由e>1,可得1<e<.11.已知△ABC外接圆O的半径为1,且OA·OB=-,∠C=,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为,则△ABC的形状为()A.直角三角形B.等边三角形C.钝角三角形D.等腰直角...