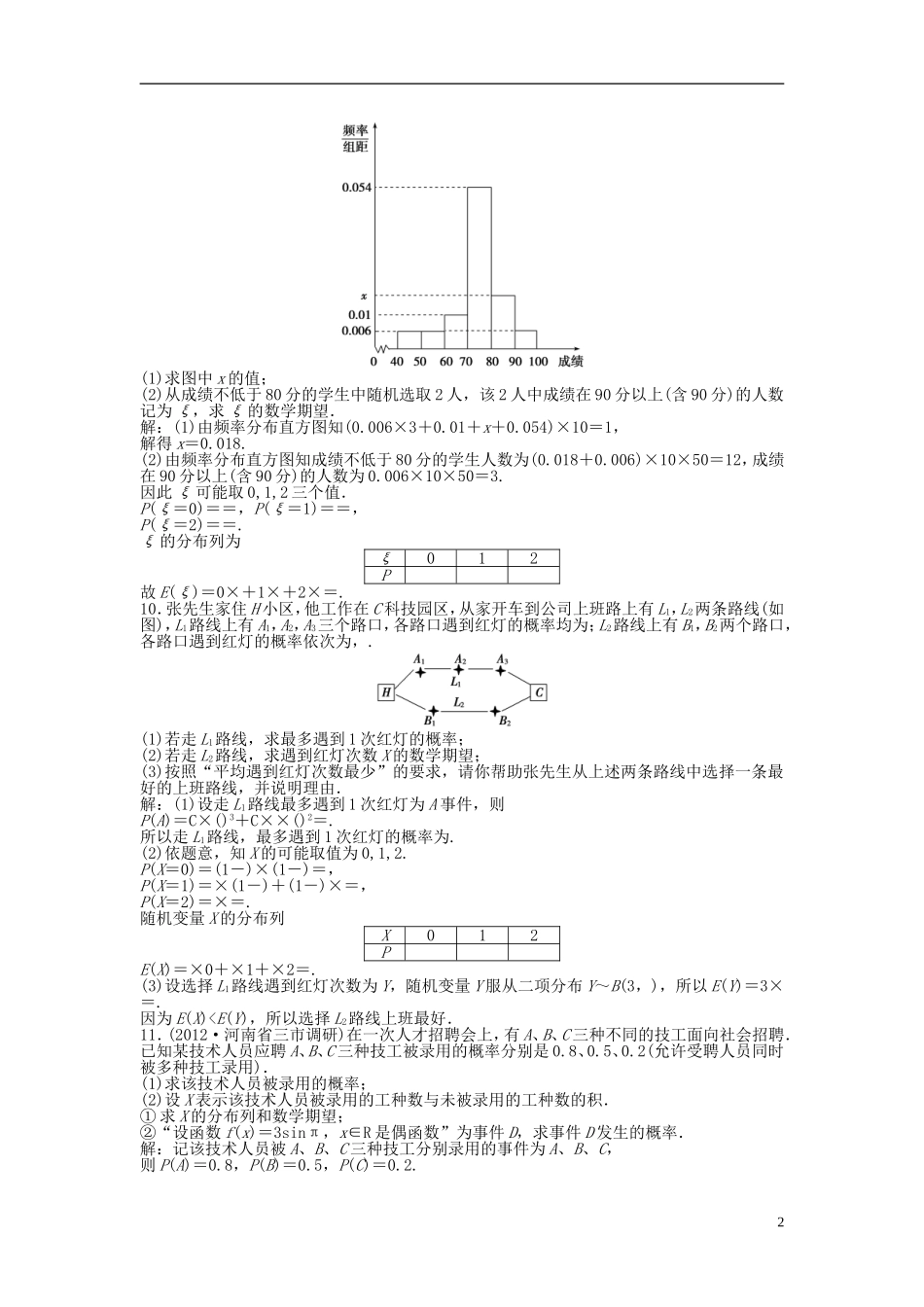
高考数学专题六第3讲知能演练轻松闯关训练题1.(2011·高考浙江卷)从装有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是()A.B.C.D.解析:选D.“所取的3个球中至少有1个白球”的对立事件是“所取的3个球都不是白球”,因而所求的概率P=1-=1-=.2.有一底面半径为1,高为2的圆柱,点O为这个圆柱底面圆的圆心,在这个圆柱内随机取一点P,则点P到点O的距离大于1的概率为()A.B.C.D.解析:选B.设点P到点O的距离小于1的概率为P1,由几何概型,则P1===,故点P到点O的距离大于1的概率P=1-=.3.(2012·安徽淮北二模)设随机变量ξ服从正态分布N(3,σ2),若P(ξ>m)=a,则P(ξ>6-m)等于()A.aB.1-2aC.2aD.1-a解析:选D.正态分布曲线关于x=μ对称,即关于x=3对称,m与6-m关于x=3对称,∴P(ξ<6-m)=P(ξ>m)=a,则P(ξ>6-m)=1-a.4.(2012·福州高三质量检查)在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为,则事件A恰好发生一次的概率为()A.B.C.D.解析:选C.设事件A在每次试验中发生的概率为x,由题意有1-C(1-x)3=,得x=,则事件A恰好发生一次的概率为C××(1-)2=.5.从1,2,3,4,5中任取两个不同的数,事件A为“取到的两个数之和为偶数”,事件B为“取到的两个数均为偶数”,则P(B|A)=()A.B.C.D.解析:选B.由于n(A)=C+C=4,n(AB)=C=1,所以P(B|A)==,故选B.6.(2012·高考上海卷)三位同学参加跳高、跳远、铅球项目的比赛.若每人都选择其中两个项目,则有且仅有两人选择的项目完全相同的概率是__________(结果用最简分数表示).解析:三位同学每人选择三项中的两项有CCC=3×3×3=27(种)选法,其中有且仅有两人所选项目完全相同的有CCC=3×3×2=18(种)选法.∴所求概率为P==.答案:7.在集合A={m|关于x的方程x2+mx+m+1=0无实根}中随机的取一元素x,恰使式子lgx有意义的概率为________.解析:由于Δ=m2-4(m+1)<0,得-10.在数轴上表示为,故所求概率为.答案:8.已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a,b,c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=“|a-b|的取值”,则X的数学期望E(X)为________.解析:依题意知>0.X可能取的值为:0,1,2,则P(X=0)==,P(X=1)==,P(X=2)==,∴E(X)=0×+1×+2×=.答案:9.(2012·高考广东卷)某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].1(1)求图中x的值;(2)从成绩不低于80分的学生中随机选取2人,该2人中成绩在90分以上(含90分)的人数记为ξ,求ξ的数学期望.解:(1)由频率分布直方图知(0.006×3+0.01+x+0.054)×10=1,解得x=0.018.(2)由频率分布直方图知成绩不低于80分的学生人数为(0.018+0.006)×10×50=12,成绩在90分以上(含90分)的人数为0.006×10×50=3.因此ξ可能取0,1,2三个值.P(ξ=0)==,P(ξ=1)==,P(ξ=2)==.ξ的分布列为ξ012P故E(ξ)=0×+1×+2×=.10.张先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1,L2两条路线(如图),L1路线上有A1,A2,A3三个路口,各路口遇到红灯的概率均为;L2路线上有B1,B2两个路口,各路口遇到红灯的概率依次为,.(1)若走L1路线,求最多遇到1次红灯的概率;(2)若走L2路线,求遇到红灯次数X的数学期望;(3)按照“平均遇到红灯次数最少”的要求,请你帮助张先生从上述两条路线中选择一条最好的上班路线,并说明理由.解:(1)设走L1路线最多遇到1次红灯为A事件,则P(A)=C×()3+C××()2=.所以走L1路线,最多遇到1次红灯的概率为.(2)依题意,知X的可能取值为0,1,2.P(X=0)=(1-)×(1-)=,P(X=1)=×(1-)+(1-)×=,P(X=2)=×=.随机变量X的分布列X012PE(X)=×0+×1+×2=.(3)设选择L1路线遇到红灯次数为Y,随机变量Y服从二项分布Y~B(3,),所以E(Y)=3×=.因为E(X)