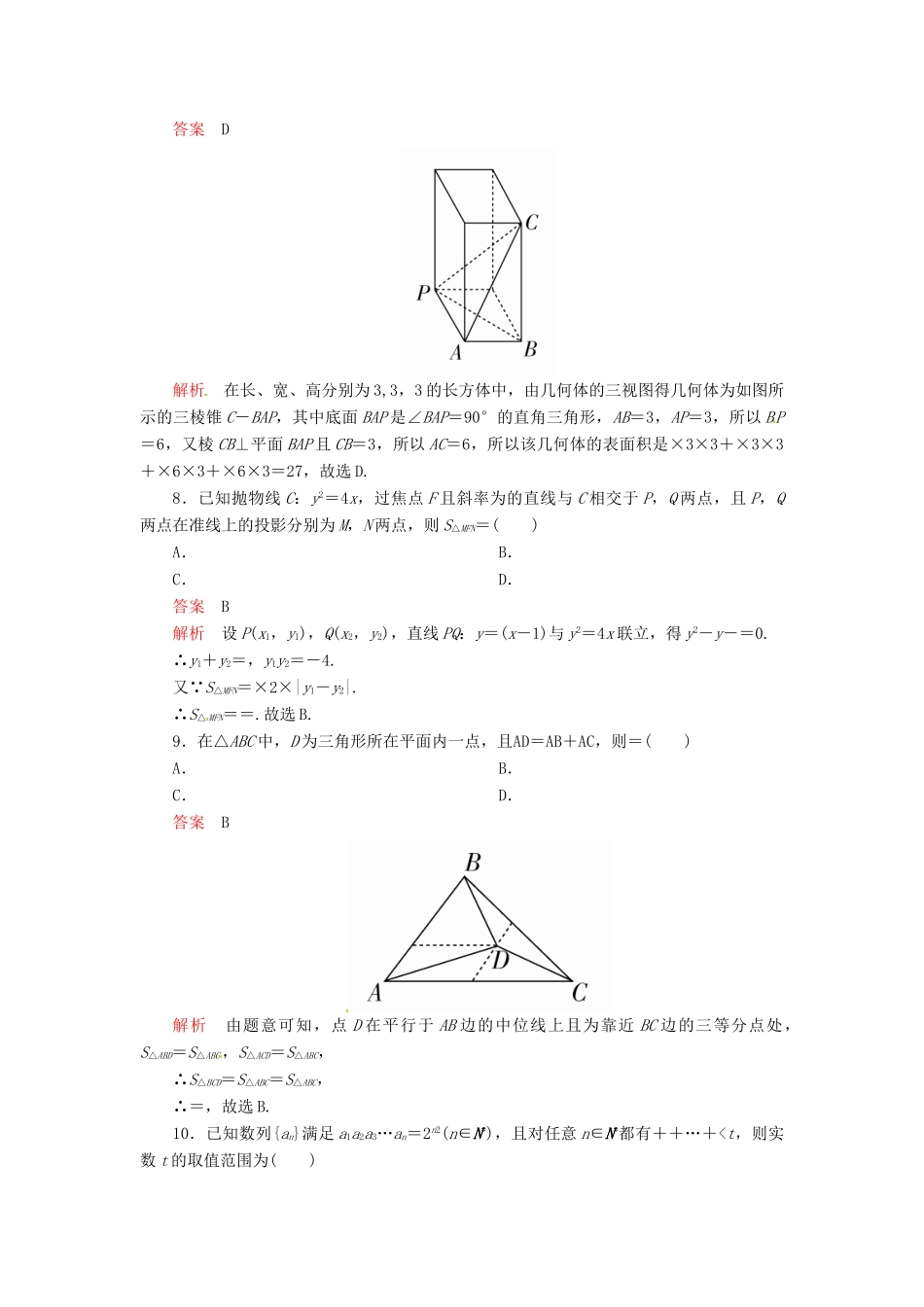
三基保分强化训练(三)1.已知=(1+i)2(i为虚数单位),则复数z的共轭复数为()A.--iB.-+iC.-iD.+i答案B解析 =(1+i)2,∴z====--i,∴z=-+i.故选B.2.已知全集U=R,集合A=,B={x|log3x<1},则A∩(∁UB)=()A.(-1,+∞)B.[3,+∞)C.(-1,0)∪(3,+∞)D.(-1,0]∪[3,+∞)答案D解析 2x>=2-1,∴x>-1,∴A={x|x>-1}.又 log3x<1,∴log3x,则下列为真命题的是()A.p∧qB.p∧(綈q)C.(綈p)∧qD.(綈p)∧(綈q)答案B解析对于命题p,当x0=0时,1≥0成立,所以命题p为真命题,命题綈p为假命题;对于命题q,当a=-1,b=1时,<,所以命题q为假命题,命题綈q为真命题,所以p∧(綈q)为真命题,故选B.4.元朝时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a,b分别为5,2,则输出的n=()A.2B.3C.4D.5答案C解析由程序框图得,n=1,a=,b=4,a≤b不成立;n=2,a=,b=8,a≤b不成立;n=3,a=,b=16,a≤b不成立;n=4,a=,b=32,a≤b成立.故输出的n=4,故选C.5.已知函数f(x)=cos(x+θ)(0<θ<π)在x=时取得最小值,则f(x)在[0,π]上的单调递增区间是()A.B.C.D.答案A解析因为0<θ<π,所以<+θ<,又f(x)=cos(x+θ)在x=时取得最小值,所以+θ=π,θ=,所以f(x)=cos.由0≤x≤π,得≤x+≤.由π≤x+≤,得≤x≤π,所以f(x)在[0,π]上的单调递增区间是,故选A.6.已知函数f(x)=kx+1,其中实数k随机选自区间[-2,1],对任意x∈[0,1],f(x)≥0的概率是()A.B.C.D.答案C解析当k=0时,f(x)=1,满足对任意x∈[0,1],f(x)≥0;当k≠0时,函数f(x)=kx+1在R上单调,所以对任意x∈[0,1],f(x)≥0等价于解得-1≤k≤1,因为实数k随机选自区间[-2,1],所以所求概率为P==.7.已知某几何体的三视图如图所示,则该几何体的表面积为()A.B.27C.27D.27答案D解析在长、宽、高分别为3,3,3的长方体中,由几何体的三视图得几何体为如图所示的三棱锥C-BAP,其中底面BAP是∠BAP=90°的直角三角形,AB=3,AP=3,所以BP=6,又棱CB⊥平面BAP且CB=3,所以AC=6,所以该几何体的表面积是×3×3+×3×3+×6×3+×6×3=27,故选D.8.已知抛物线C:y2=4x,过焦点F且斜率为的直线与C相交于P,Q两点,且P,Q两点在准线上的投影分别为M,N两点,则S△MFN=()A.B.C.D.答案B解析设P(x1,y1),Q(x2,y2),直线PQ:y=(x-1)与y2=4x联立,得y2-y-=0.∴y1+y2=,y1y2=-4.又 S△MFN=×2×|y1-y2|.∴S△MFN==.故选B.9.在△ABC中,D为三角形所在平面内一点,且AD=AB+AC,则=()A.B.C.D.答案B解析由题意可知,点D在平行于AB边的中位线上且为靠近BC边的三等分点处,S△ABD=S△ABC,S△ACD=S△ABC,∴S△BCD=S△ABC=S△ABC,∴=,故选B.10.已知数列{an}满足a1a2a3…an=2n2(n∈N*),且对任意n∈N*都有++…+