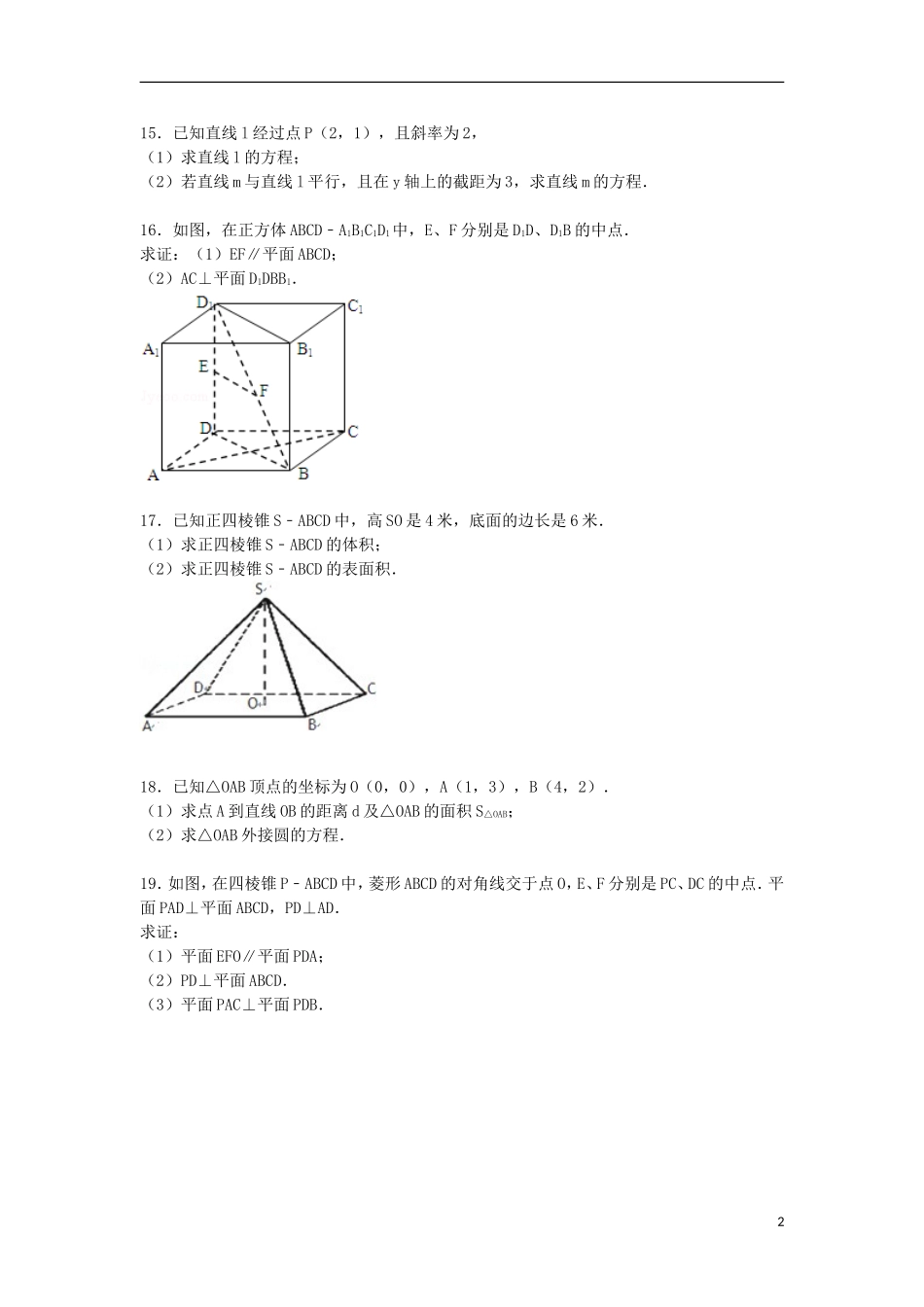
2014-2015学年江苏省南京六中高一(下)期末数学试卷一、填空题(本大题共14小题,每小题5分,共70分,请将答案写在答卷纸相应区域)1.在等差数列{an}中,已知a1=1,d=2,则第3项a3=.2.过两点(1,0),(0,2)的直线方程是.3.一元二次不等式(x﹣2)(x﹣3)<0的解集为.4.直线的倾斜角的大小为.5.在等比数列{an}中,已知a1=2,q=2,an=16,则项数n=.6.两条平行直线3x﹣4y+12=0与3x﹣4y+2=0之间的距离d=.7.在△ABC中,A=30°,C=45°,c=,则边a=.8.在正方体ABCD﹣A1B1C1D1中,直线AD1与平面ABCD所成的角的大小为.9.在△ABC中,已知a=1,b=2,C=60°,则c=.10.过点A(2,3),且与直线x﹣y﹣1=0垂直的直线方程是.11.在等差数列{an}中,a3+a9=4,则前11项的和S11=.12.以点X(3,1)为圆心,且与x轴相切的圆的方程是.13.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:则第n个图案中有白色地面砖块14.已知两条不同直线m、l,两个不同平面α、β,给出下列命题:①若l垂直于α内的两条相交直线,则l⊥α;②若l∥α,则l平行于α内的所有直线;③若m⊂α,l⊂β且l⊥m,则α⊥β;④若l⊂β,l⊥α,则α⊥β;⑤若m⊂α,l⊂β且α∥β,则m∥l.其中正确命题的序号是.(把你认为正确命题的序号都填上)二、解答题(本大题共6小题,每小题15分,共90分,请将答案写在答卷纸相应区域,解答时应写出文字说明、证明或演算步骤)115.已知直线l经过点P(2,1),且斜率为2,(1)求直线l的方程;(2)若直线m与直线l平行,且在y轴上的截距为3,求直线m的方程.16.如图,在正方体ABCD﹣A1B1C1D1中,E、F分别是D1D、D1B的中点.求证:(1)EF∥平面ABCD;(2)AC⊥平面D1DBB1.17.已知正四棱锥S﹣ABCD中,高SO是4米,底面的边长是6米.(1)求正四棱锥S﹣ABCD的体积;(2)求正四棱锥S﹣ABCD的表面积.18.已知△OAB顶点的坐标为O(0,0),A(1,3),B(4,2).(1)求点A到直线OB的距离d及△OAB的面积S△OAB;(2)求△OAB外接圆的方程.19.如图,在四棱锥P﹣ABCD中,菱形ABCD的对角线交于点O,E、F分别是PC、DC的中点.平面PAD⊥平面ABCD,PD⊥AD.求证:(1)平面EFO∥平面PDA;(2)PD⊥平面ABCD.(3)平面PAC⊥平面PDB.220.如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ过点C,其中AB=30米,AD=20米.记三角形花园APQ的面积为S.(1)设DQ=x米,将S表示成x的函数.(2)当DQ的长度是多少时,S最小?并求S的最小值.(3)要使S不小于1600平方米,则DQ的长应在什么范围内?32014-2015学年江苏省南京六中高一(下)期末数学试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,共70分,请将答案写在答卷纸相应区域)1.在等差数列{an}中,已知a1=1,d=2,则第3项a3=5.考点:等差数列的通项公式.专题:等差数列与等比数列.分析:直接由已知写出等差数列的通项公式,取n=3得答案.解答:解:在等差数列{an}中,由a1=1,d=2,得an=a1+(n﹣1)d=1+2(n﹣1)=2n﹣1,∴第3项a3=2×3﹣1=5.故答案为:5.点评:本题考查了等差数列的通项公式,是基础的计算题,属会考题型.2.过两点(1,0),(0,2)的直线方程是2x+y﹣2=0.考点:直线的两点式方程.专题:计算题.分析:由斜率公式可得斜率,由点斜式可得方程,化为一般式即可.解答:解:由题意可得直线的斜率k==﹣2,故直线的方程为:y﹣2=﹣2(x﹣0)整理可得2x+y﹣2=0故答案为:2x+y﹣2=0点评:本题考查直线方程的求解,结果化为一般式方程,属基础题.3.一元二次不等式(x﹣2)(x﹣3)<0的解集为{x|2<x<3}.考点:一元二次不等式的解法.专题:不等式的解法及应用.分析:根据一元二次不等式与对应方程解的关系,写出不等式的解集即可.解答:解:一元二次不等式(x﹣2)(x﹣3)<0,对应的方程为(x﹣2)(x﹣3)=0,解方程,得x=2,或x=3,所以,不等式(x﹣2)(x﹣3)<0的解集为{x|2<x<3}.故答案为:{x|2<x<3}.点评:本题考查了求一元二次不等式的解集的应用问题...