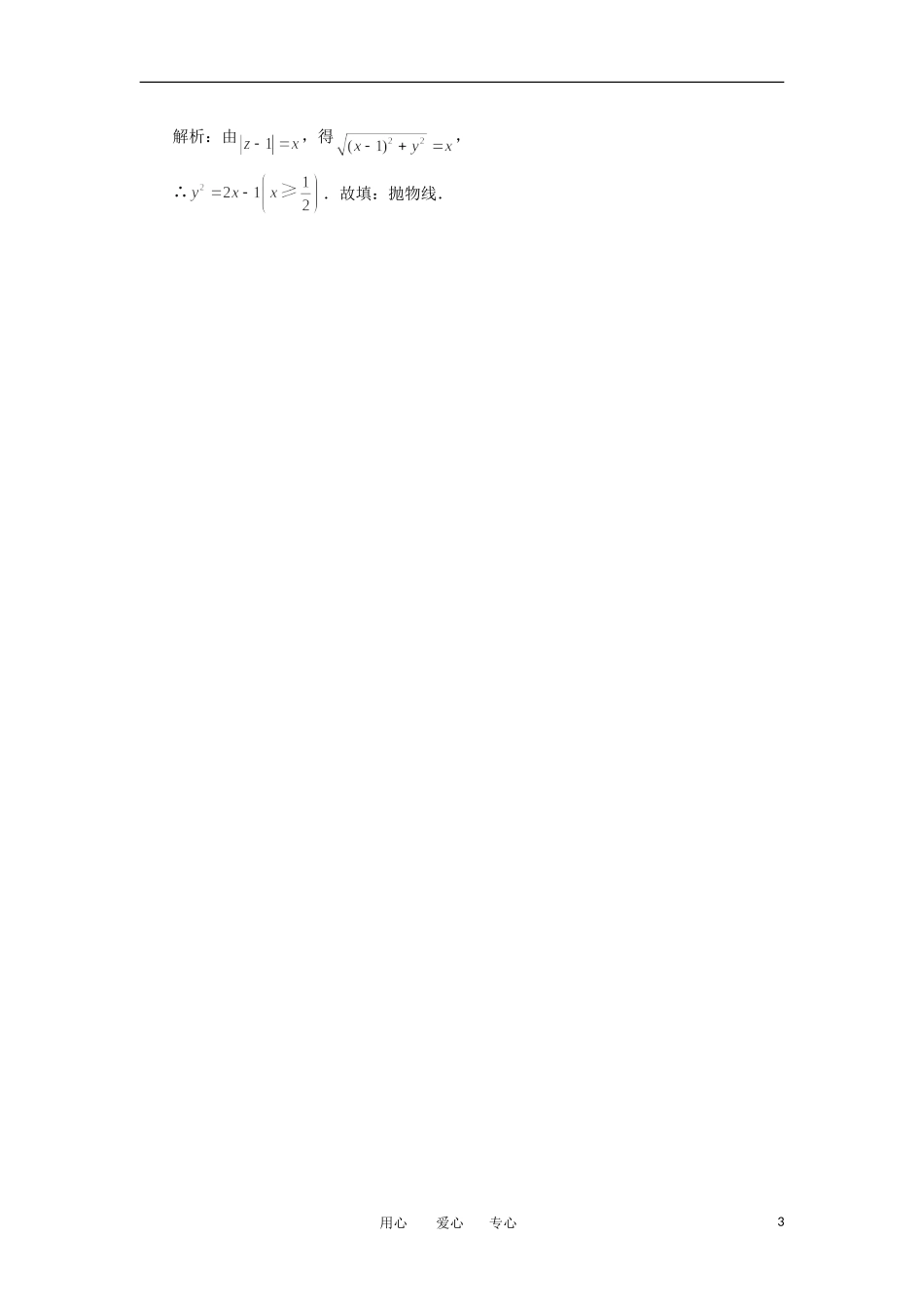
填空题的解答技巧与方法填空题不同于解答题,它只要求直接写出结果,不必写出计算或推理过程,故填空题的结果必须是数值准确,形式规范,表达式最简.基于以上原因,现就填空题的特点及方法技巧试作分析.一、填空题的主要特点填空题的主要特点是题目小、跨度大、知识覆盖面广,渗透着各种思想与方法,形式灵活,突出考查学生准确、严谨、全面、灵活运用知识的能力,近年来填空题作为命题组改革试验的一个窗口,因此出现了不少创新题型:如阅读理解型、发散开放型、多项选择型、实际应用型等,这些题型的出现,使解填空题的要求更高、更严了.二、填空题的解答技巧与方法1.直接法从题设条件出发,运用定义、定理、公式、性质、法则等知识,通过变形、推理、计算等,得到正确的结论.直接法是解填空题的常用的基本方法.使用时,要善于透过现象抓本质,自觉地、有意识地采用灵活、简捷的解法.例1设是虚数,条件甲:是实数,条件乙:,则甲是乙的条件.解析:设是虚数..若,即,则,若,则,又,.甲是乙的充要条件.例2①;②;③;④中,使成立的是.解析:,,即.2.数形结合法根据题设条件的几何意义,画出辅助图形,然后通过对图形的直观分析,获取正确答案.这种方法常常会收到简捷明快的效果.例3已知,,则.解析:由联想复数加法的几何性质,不难发现所对应的三点及原点构成平行四边形的四个顶点如图,用心爱心专心1则为等边三角形易求得;当点对应的点在实轴下方时,,故填或.例4适合条件及的复数的集合.解析:由数形结合知,表示单位圆,变形为,其几何意义为与1两点连线的垂直平分线,即轴,则易知点为单位圆与轴的两个交点,.即复数的集合为.3.等价转化运用转化的方法,把新问题转化为已经解决的问题,许多问题是在条件和结论不断转化中获得解决的.例5复数满足,则等于.解析:利用复数相等的定义求复数的关键是要把两个复数转化成代数形式.设,则,所以.例6设,则方程的解的个数为.解析:由,知.或为纯虚数.设,有或.方程有3个解.点评:本例中,充分注意到了的特征,设,简化了运算过程,也考查了同学们的观察能力.4.用好已知条件速解创新填空题填空题作为试验田,常有创新题出现,这类题目,通过定义、新概念或一种新的运算,或给定新模型来创设问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识与方法,实现信息的迁移,从而顺利解决问题.例7定义运算,则对复数,符合条件的点在复平面上所表示的曲线形状是.用心爱心专心2解析:由,得,.故填:抛物线.用心爱心专心3