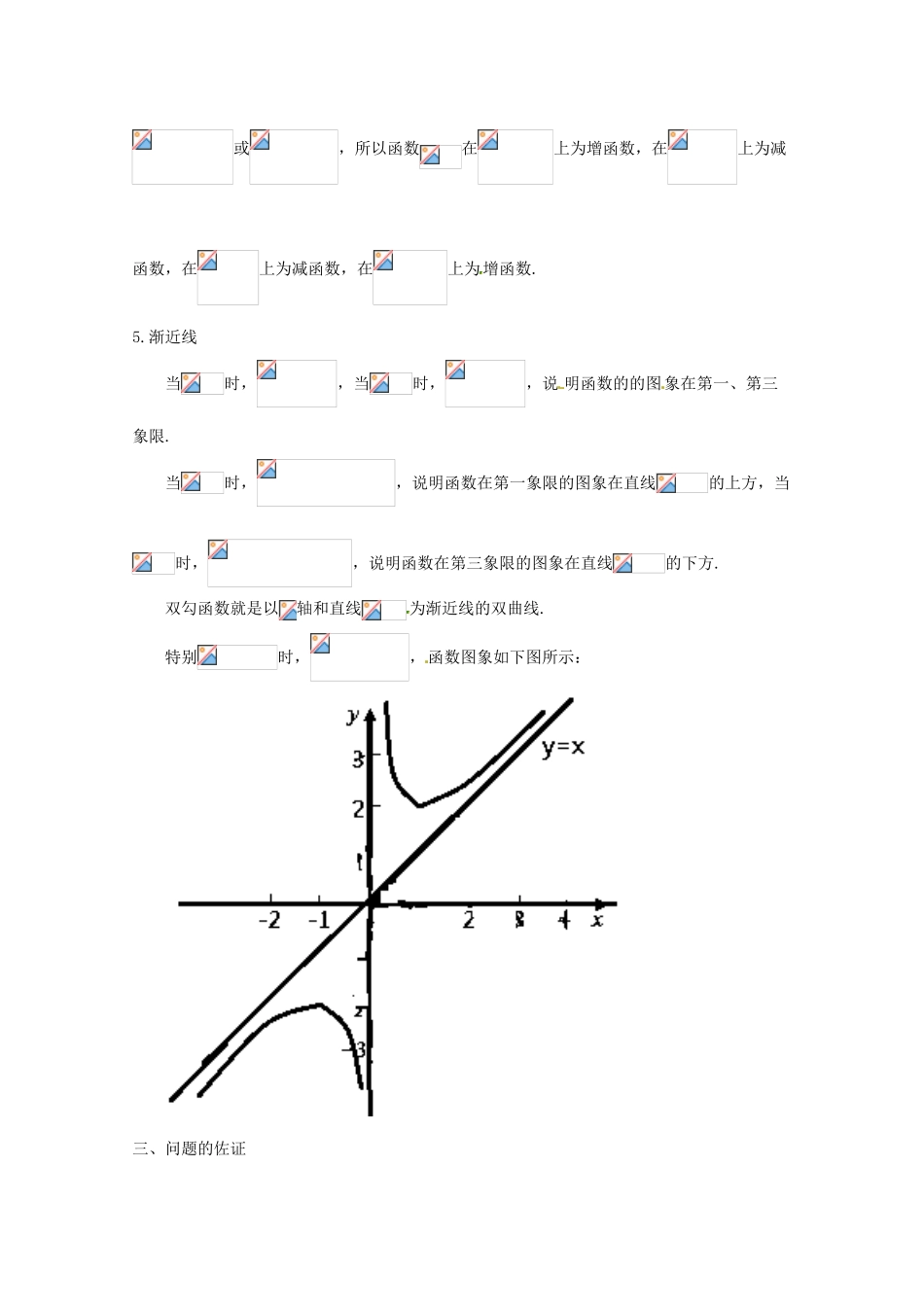
问题5深化点对号函数的应用一、问题的提出在不等式恒成立和有解问题中会涉及到利用对号函数求最值问题,所以掌握对号函数图象和性质至关重要,本文列举了对号函数的应用,以飨读者.二、问题的探源(1)对勾函数的定义形如的函数,叫做对勾函数.(2)对勾函数的图象与性质1.定义域2.值域当时,(当且仅当,即时取等号).当时,(当且仅当,即时取等号).函数的值域为.3.奇偶性由于双勾函数定义域关于原点对称,,则对勾函数为奇函数.4.单调性由于,令,解得或,令,解得或,所以函数在上为增函数,在上为减函数,在上为减函数,在上为增函数.5.渐近线当时,,当时,,说明函数的的图象在第一、第三象限.当时,,说明函数在第一象限的图象在直线的上方,当时,,说明函数在第三象限的图象在直线的下方.双勾函数就是以轴和直线为渐近线的双曲线.特别时,,函数图象如下图所示:三、问题的佐证(一)恒成立问题中的对号函数问题例1.若函数在区间上单调递减,则实数t的取值范围是()A.B.C.D.【答案】C(二)有解问题中的对号函数问题例2.若二次不等式在区间[2,5]上有解,则的取值范围是A.B.C.D.【答案】A【解析】关于不等式在上有解,所以在上有解,即在上有解,设,所以恒成立,所以函数在上单调递减函数,所以函数的值域为,所以,故选A.(三)对号函数在数列最值问题中的应用数列满足,则的最小值为__________.【答案】21四、问题的解决1.已知,,则()A.B.C.D.【答案】A2.已知,则有()A.最大值B.最小值C.最大值2D.最小值2【答案】D【解析】依题意,类比对钩函数的性质可知,当,即时,函数取得最小值为.3.已知x>0,则的最大值为________.【答案】【解析】∵x>0∴当且仅当即x=2时取等号故的最大值为故答案为:.4.已知函数,,则的最小值是__________.【答案】【解析】∵,∴,当且仅当,即时,等号成立,故的最小值是,故答案为.5.要制作一个容积为4m3,高为1m的无盖长方体容器.已知该容器的底面造价是每平方米200元,侧面造价是每平方米100元,则该容器的最低总造价是________元.【答案】16006.已知函数,,.(1)求实数的值;(2)若函数,求的最小值并指出此时的取值.【解析】(1)得到b=1,c=7;(2),当且仅当时等号成立.7.函数的最大值为______【答案】【解析】设即求函数在[1,2]上的最大值函数为对勾函数,在上单调递减。所以当t=1时,函数取到最大值,即8.已知,且,若不等式恒成立,求实数的取值范围.【答案】9.已知,若对所有的均成立,求实数的取值范围.解:由题易知,令,,当且仅当时取等号所以,即.10.某工厂去年的某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第次投入后,每只产品的固定成本为(为常数,且),若产品销售价保持不变,第次投入后的年利润为万元.(1)求的值,并求出的表达式;(2)问从今年算起第几年利润最高?最高利润为多少万元?解:(1)由,当时,由题意,可得,所以(2)由当且仅当,即时取等号,所以第8年工厂的利润最高,最高为520万元.11.已知在区间单调递增,求的取值范围.解:当时,在区间显然单调递增;当时,结合的图像与性质,可知函数在区间单调递增当时在区间内单调递增,所以,所以综上所述,实数的取值范围为.12.求函数的值域.解:,令,则,结合图像与性质,可知当时函数单调递减,当时函数单调递增,又,所以13.已知函数f(x)=,其中x∈[2,+∞).(1)求f(x)的最小值;(2)若f(x)>a恒成立,求a的取值范围.(2)∵f(x)的最小值为,∴f(x)>a恒成立,只需f(x)min>a,即a<.故a的取值范围为.