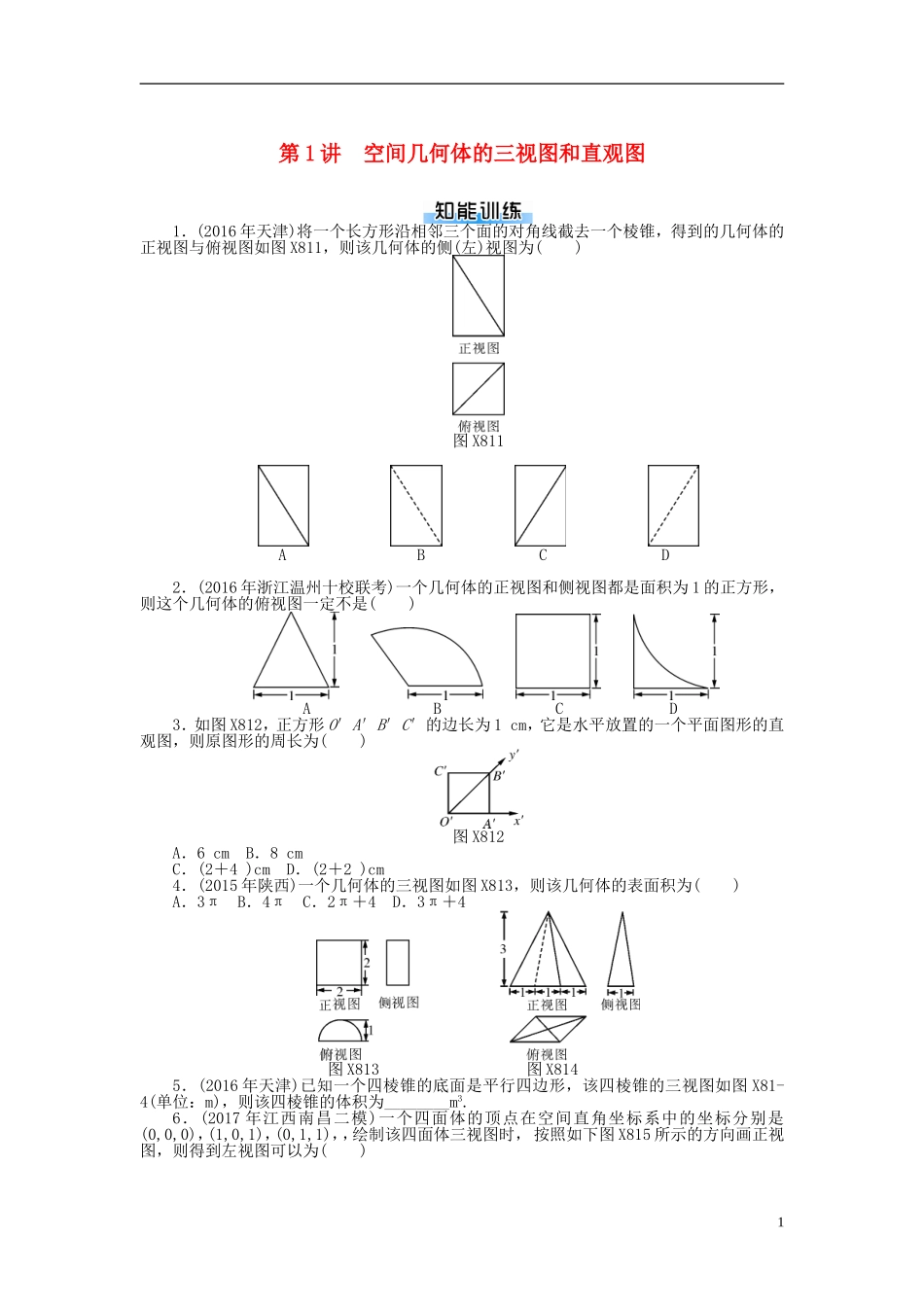
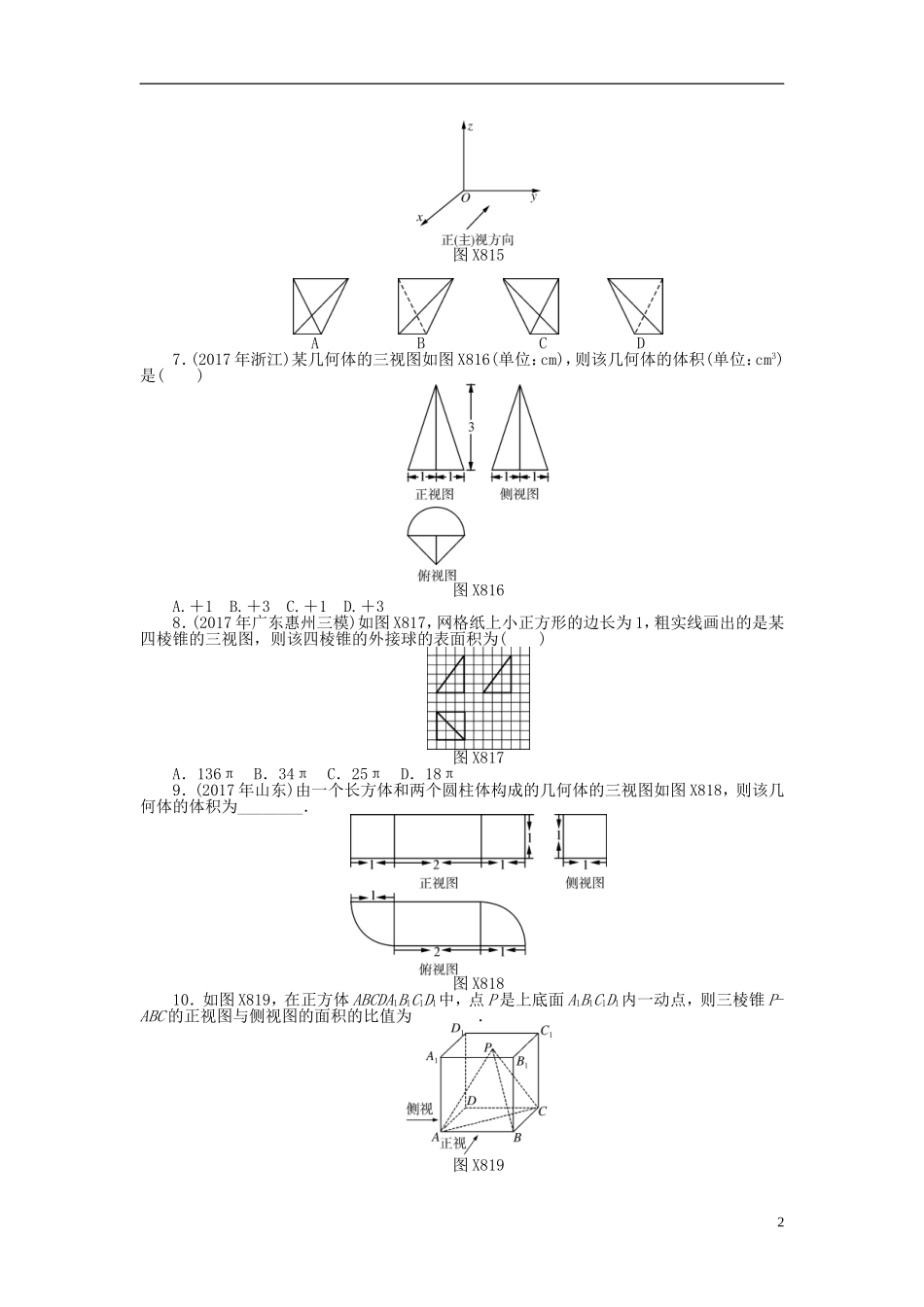
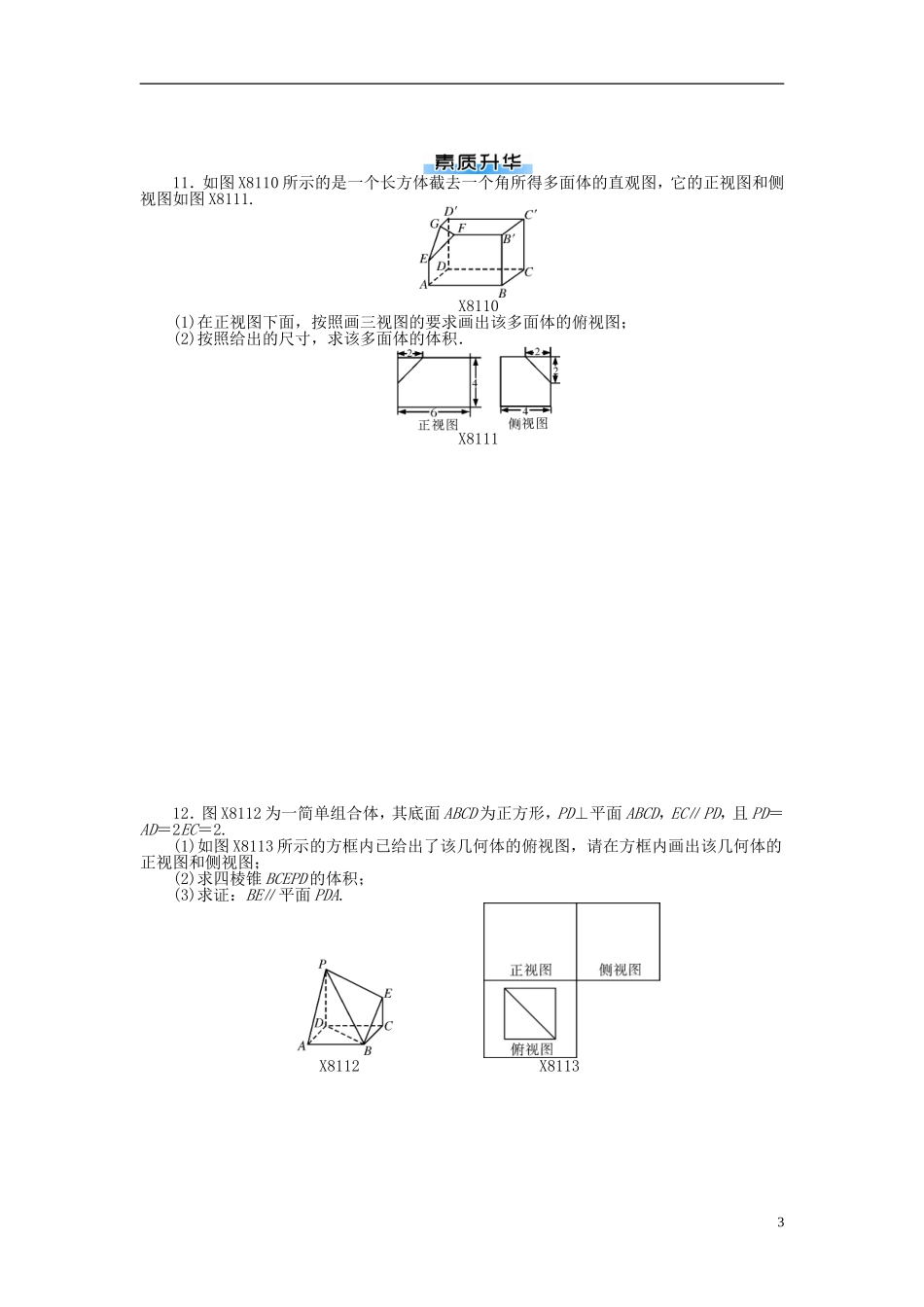
第1讲空间几何体的三视图和直观图1.(2016年天津)将一个长方形沿相邻三个面的对角线截去一个棱锥,得到的几何体的正视图与俯视图如图X811,则该几何体的侧(左)视图为()图X811ABCD2.(2016年浙江温州十校联考)一个几何体的正视图和侧视图都是面积为1的正方形,则这个几何体的俯视图一定不是()ABCD3.如图X812,正方形O′A′B′C′的边长为1cm,它是水平放置的一个平面图形的直观图,则原图形的周长为()图X812A.6cmB.8cmC.(2+4)cmD.(2+2)cm4.(2015年陕西)一个几何体的三视图如图X813,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4图X813图X8145.(2016年天津)已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图X81-4(单位:m),则该四棱锥的体积为________m3.6.(2017年江西南昌二模)一个四面体的顶点在空间直角坐标系中的坐标分别是(0,0,0),(1,0,1),(0,1,1),,绘制该四面体三视图时,按照如下图X815所示的方向画正视图,则得到左视图可以为()1图X815ABCD7.(2017年浙江)某几何体的三视图如图X816(单位:cm),则该几何体的体积(单位:cm3)是()图X816A.+1B.+3C.+1D.+38.(2017年广东惠州三模)如图X817,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的外接球的表面积为()图X817A.136πB.34πC.25πD.18π9.(2017年山东)由一个长方体和两个圆柱体构成的几何体的三视图如图X818,则该几何体的体积为________.图X81810.如图X819,在正方体ABCDA1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-ABC的正视图与侧视图的面积的比值为________.图X819211.如图X8110所示的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图如图X8111.X8110(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积.X811112.图X8112为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2.(1)如图X8113所示的方框内已给出了该几何体的俯视图,请在方框内画出该几何体的正视图和侧视图;(2)求四棱锥BCEPD的体积;(3)求证:BE∥平面PDA.X8112X81133第1讲空间几何体的三视图和直观图1.B解析:截去的是长方体右上方顶点.故选B.2.B解析:由题意,符合选项A的几何体是一个直三棱柱,其中底面三角形是底边为1,高为1的等腰三角形,侧棱长为1;符合选项C的几何体是一个棱长为1的正方体;符合选项D的几何体是一个棱长为1的正方体去掉半径与母线长都为1的圆柱.3.B4.D解析:由三视图知:该几何体是半个圆柱,其中底面圆的半径为1,母线长为2,所以该几何体的表面积是×2π×1×2+π×12+2×2=3π+4.故选D.5.2解析:由三视图知四棱锥高为3,底面平行四边形的底为2,高为1,因此体积为×(2×1)×3=2.故答案为2.6.B解析:满足条件的四面体如图D138(1),依题意投影到yOz平面为正投影,所以左(侧)视方向如图,所以得到左视图效果如图D138(2),故答案:选B.(1)(2)图D1387.A解析:V=×3×=+1.8.B解析:画出满足条件的四棱锥D139,底面是边长为3的正方形,顶点在底面的射影为点B,高为4.根据垂直关系可得AD⊥AE,DC⊥EC,DE为直角三角形△ADE和△CDE和△BDE的公共斜边,所以取DE中点O,O为四棱锥外接圆的圆心,DE2=AB2+BE2+AD2=32+42+32=34,DE=2R=,那么四棱锥外接球的表面积为S=4πR2=34π.故选B.图D1399.2+解析:该几何体的体积为π×12×1×2+2×1×1=+2.10.1解析:三棱锥PABC的正视图与侧视图为底边和高均相等的三角形,故它们的面积相等,面积比值为1.11.解:(1)如图D140.(2)所求多面体体积V=V长方体-V正三棱锥=4×4×6-××2=.图D14012.(1)解:该组合体的正视图和侧视图如图D141.4图D141(2)解:∵PD⊥平面ABCD,PD⊂平面PDCE,∴平面PDCE⊥平面ABCD.∵平面PDCE∩平面ABCD=CD,∵BC⊥CD,∴BC⊥平面PDCE.∵S梯形PDCE=(PD+EC)·DC=×3×2=3,∴四棱锥BCEPD的体积为VBCEPD=S梯形PDCE·BC=×3×2=2.(3)证明:∵EC∥PD,PD⊂平面PDA,EC⊄平面PDA,∴EC∥平面PDA.同理,BC∥平面PDA.∵EC⊂平面EBC,BC⊂平面EBC,且EC∩BC=C,∴平面EBC∥平面PDA.又∵BE⊂平面EBC,∴BE∥平面PDA.5