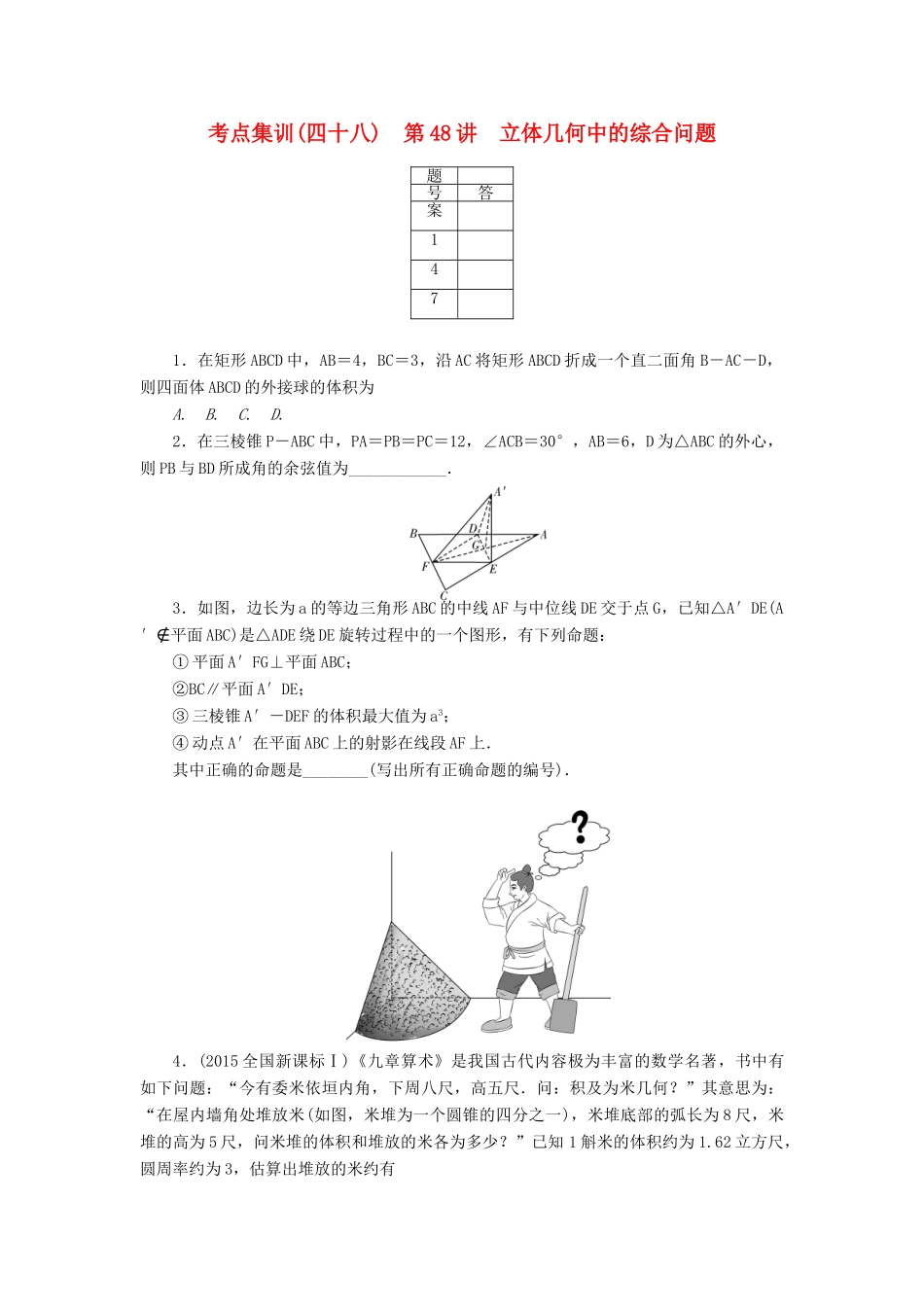
考点集训(四十八)第48讲立体几何中的综合问题题号答案1471.在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为A.B.C.D.2.在三棱锥P-ABC中,PA=PB=PC=12,∠ACB=30°,AB=6,D为△ABC的外心,则PB与BD所成角的余弦值为____________.3.如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:①平面A′FG⊥平面ABC;②BC∥平面A′DE;③三棱锥A′-DEF的体积最大值为a3;④动点A′在平面ABC上的射影在线段AF上.其中正确的命题是________(写出所有正确命题的编号).4.(2015全国新课标Ⅰ)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有A.14斛B.22斛C.36斛D.66斛5.一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________m3.6.如图,矩形ABCD中,AB=2,BC=4,将△ABD沿对角线BD折起到△A′BD的位置,使点A′在平面BCD内的射影点O恰好落在BC边上,则异面直线A′B与CD所成角的大小为________.7.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为A.B.16πC.9πD.8.如图,在四棱锥ABCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=.(1)证明:AC⊥平面BCDE;(2)求三棱锥E-ABC的体积.9.如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,点F在CE上,且BF⊥平面ACE.(1)证明:平面ADE⊥平面BCE;(2)求点D到平面ACE的距离.第48讲立体几何中的综合问题【考点集训】1.C2.3.①②③④4.B5.6.90°7.A8.【解析】(1)证明:如图,连接BD,在直角梯形BCDE中,由DE=BE=1,CD=2,得BD=BC=.由AC=,AB=2,得AB2=AC2+BC2,即AC⊥BC.又平面ABC⊥平面BCDE,从而AC⊥平面BCDE.(2)连EC,在Rt△ACB中,由AC=,AB=2⇒BC=,又由BD⊥BC,∠EBD=45°可知∠EBC=135°故S△BEC=×1××sin135°=故VE-ABC=VA-BEC=××=.9.【解析】(1)因为BF⊥平面ACE,所以BF⊥AE.因为平面ABCD⊥平面ABE,BC⊥AB,平面ABCD∩平面ABE=AB,所以BC⊥平面ABE,从而BC⊥AE.于是AE⊥平面BCE,故平面ADE⊥平面BCE.(2)方法一:连结BD交AC于点M,则点M是BD的中点,所以点D与点B到平面ACE的距离相等.因为BF⊥平面ACE,所以BF为点B到平面ACE的距离.因为AE⊥平面BCE,所以AE⊥BE.又AE=BE,所以△AEB是等腰直角三角形.因为AB=2,所以BE=2sin45°=.在Rt△CBE中,CE==.所以BF===.故点D到平面ACE的距离是.方法二:过点E作EG⊥AB,垂足为G,因为平面ABCD⊥平面ABE,所以EG⊥平面ABCD.因为AE⊥平面BCE,所以AE⊥BE.又AE=BE,所以△AEB是等腰直角三角形,从而G为AB的中点.又AB=2,所以EG=1.因为AE⊥平面BCE,所以AE⊥EC.又AE=BE=2sin45°=,CE==.设点D到平面ACE的距离为h,因为VD-ACE=VE-ACD,则S△ACE·h=S△ACD·EG.所以h===,故点D到平面ACE的距离是.