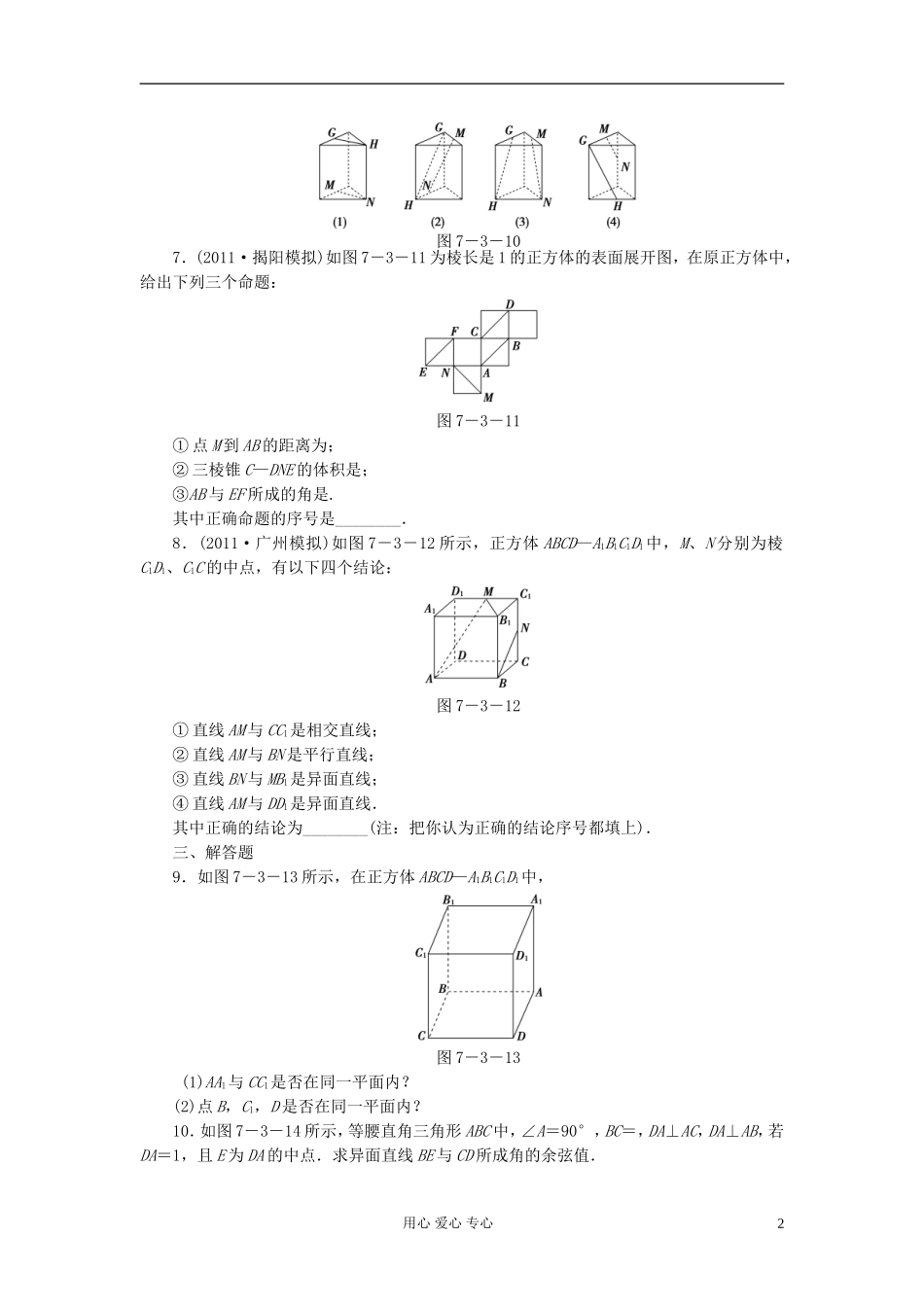
一、选择题1.(2010·山东高考)在空间,下列命题正确的是()A.平行直线的平行投影重合B.平行于同一直线的两个平面平行C.垂直于同一平面的两个平面平行D.垂直于同一平面的两条直线平行2.如图7-3-8,α∩β=l,A、B∈α,C∈β,且C∉l,直线AB∩l=M,过A、B、C三点的平面记作γ,则γ与β的交线必通过()图7-3-8A.点AB.点BC.点C但不过点MD.点C和点M3.已知a、b是异面直线,直线c∥直线a,那么c与b()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线4.平行六面体底面是平行四边形的四棱柱ABCD—A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为()A.3B.4C.5D.65.(2011·济南模拟)如图7-3-9:四面体P—ABC为正四面体,M为PC的中点,则BM与AC所成的角的余弦值为()图7-3-9A.B.C.D.0二、填空题6.如图7-3-10所示,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异面直线的图形有________(填上所有正确答案的序号).用心爱心专心1图7-3-107.(2011·揭阳模拟)如图7-3-11为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:图7-3-11①点M到AB的距离为;②三棱锥C—DNE的体积是;③AB与EF所成的角是.其中正确命题的序号是________.8.(2011·广州模拟)如图7-3-12所示,正方体ABCD—A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:图7-3-12①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为________(注:把你认为正确的结论序号都填上).三、解答题9.如图7-3-13所示,在正方体ABCD—A1B1C1D1中,图7-3-13(1)AA1与CC1是否在同一平面内?(2)点B,C1,D是否在同一平面内?10.如图7-3-14所示,等腰直角三角形ABC中,∠A=90°,BC=,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.用心爱心专心2图7-3-1411.(2011·上海十四校联考)如图7-3-15,三棱锥P—ABC中,PA⊥平面ABC,∠BAC=60°,PA=AB=AC=2,E是PC的中点.图7-3-15(1)求异面直线AE和PB所成的角的余弦值;(2)求三棱锥A—EBC的体积.用心爱心专心3答案及解析1.【解】选项A,平行直线的平行投影可以依然是两条平行直线;选项B,两个相交平面的交线与某一条直线平行,则这条直线平行于这两个平面;选项C,两个相交平面可以同时垂直于同一个平面;选项D正确.【答案】D2.【解】易知γ过C点,且M∈AB,∴M∈γ,∴γ也过M点.【答案】D3.【解】若c∥b, c∥a,∴a∥b,与a,b异面矛盾.∴c,b不可能是平行直线.【答案】C4.【解】BC,BB1,AA1,DC,D1C1共5条直线条件条件.【答案】C5.【解】取AP中点N,连接MN,BN. M为PC的中点,∴MN∥AC.∴∠BMN或其补角为BM、AC所成的角. 四面体P—ABC为正四面体,设棱长为2,则BM=,MN=1,BN=,在△BMN中,cos∠BMN===.【答案】B6.【解】图(1)中,直线GH∥MN;图(2)中,G、H、N三点共面,但M∉面GHN,因此直线GH与MN异面;图(3)中,连接MG,GM∥HN,因此GH与MN共面;用心爱心专心4图(4)中,G、M、N共面,但H∉面GMN,∴GH与MN异面.所以图(2)、(4)中GH与MN异面.【答案】(2)、(4)7.【解】依题意可作出正方体的直观图,显然M到AB的距离为MC=,∴①正确,而VC—DNE=××1×1×1=,∴②正确,AB与EF所成角为AB与MC所成的角,即为.【答案】①②③8.【解】由图可知AM与CC1是异面直线,AM与BN是异面直线,BN与MB1为异面直线,AM与DD1是异面直线,故正确的结论为③④.【答案】③④9.【解】(1)在正方体ABCD—A1B1C1D1中, AA1∥CC1,∴由推论3可知,AA1与CC1可确定平面ACC1A1,∴AA1与CC1在同一平面内.(2) 点B,C1,D不共线,由公理2可知,点B,C1,D可确定平面BC1D,∴点B,C1,D在同一平面内.10.【解】取AC的中点F,连接EF,BF,在△ACD中,E、F分别是AD、AC的中点,∴EF∥CD.∴∠BEF即为异面直线BE与CD所成的角或其补角.在Rt△EAB中,AB=AC=1,AE=AD=,∴BE=.在Rt△EAF中,AF=AC=,AE=,∴EF=.在Rt△BAF中,AB=1,AF=,∴BF=.在等...