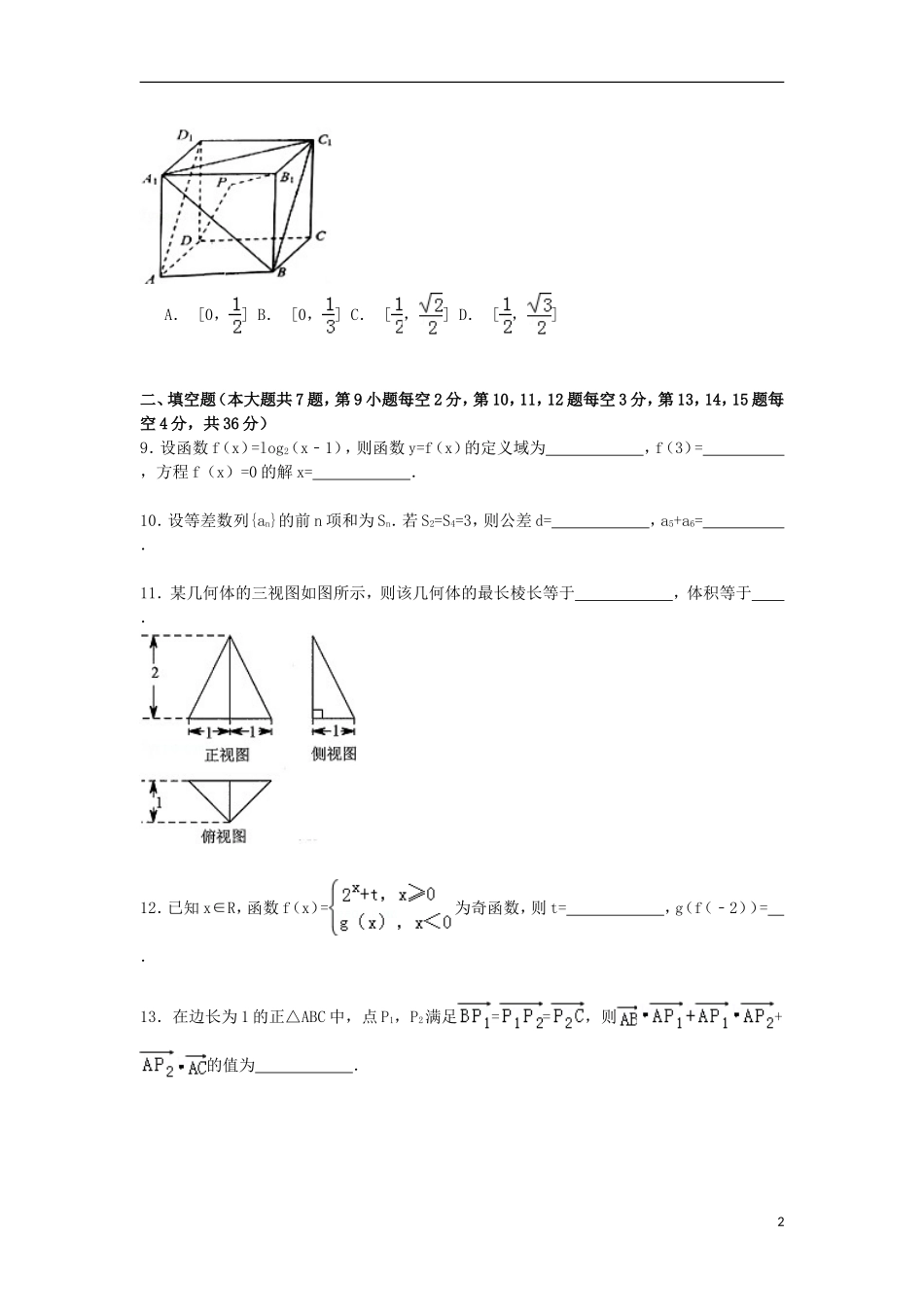
2015年浙江省绍兴市高考数学一模试卷(理科)一、选择题(共8小题,每小题3分,满分24分)1.若x∈R,则“x>1”,则“x2>1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件2.某快递公司快递一件物品的收费规定:物品不超过5千克,每件收费12元,超过5千克且不超过10千克,则超出部分每千克加收1.2元;…,现某人快递一件8千克物品需要的费用为()A.9.6元B.12元C.15.6元D.21.6元3.已知实数x,y满足,则x﹣y的最大值为()A.﹣1B.0C.1D.24.已知抛物线C:y2=4x的焦点为F,过点F的直线且交抛物线C于A,B两点,若线段AB中点的横坐标为2,则|AB|=()A.4B.6C.8D.105.已知函数f(x)=sin(x+φϖ)(ϖ>0,﹣<φ<)的最小正周期是π,且当x=时,f(x)取得最大值,则f(+x)+f(﹣x)=()A.﹣1B.0C.1D.26.在△ABC中,AB=AC,AC边上的中线长为9,当△ABC的面积最大时,AB的长为()A.9B.9C.6D.67.已知和是互相垂直的单位向量,向量满足:=n,=2n,n∈N*,设θn为﹣和﹣的夹角,则()A.θn随着n的增大而增大B.θn随着n的增大而减小C.随着n的增大,θn先增大后减小D.随着n的增大,θn先减小后增大8.如图,在棱长为3的正方体ABCD﹣A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=2+,则直线B1P与直线AD1所成角的余弦值的取值范围为()1A.[0,]B.[0,]C.[,]D.[,]二、填空题(本大题共7题,第9小题每空2分,第10,11,12题每空3分,第13,14,15题每空4分,共36分)9.设函数f(x)=log2(x﹣1),则函数y=f(x)的定义域为,f(3)=,方程f(x)=0的解x=.10.设等差数列{an}的前n项和为Sn.若S2=S4=3,则公差d=,a5+a6=.11.某几何体的三视图如图所示,则该几何体的最长棱长等于,体积等于.12.已知x∈R,函数f(x)=为奇函数,则t=,g(f(﹣2))=.13.在边长为1的正△ABC中,点P1,P2满足==,则+的值为.214.已知双曲线﹣=1(a>0,b>0)的左、右焦点分别为F1,F2,过F2作斜率为﹣2的直线交双曲线的渐近线于P,Q两点,M为线段PQ的中点,若直线MF1平行于其中一条渐近线,则该双曲线的离心率为.15.当且仅当x∈(a,b)∪(c,d)(其中b≤c)时,函数f(x)=2x2+x+2的图象在函数g(x)=|2x+1|+|x﹣t|图象的下方,则b﹣a+d﹣c的取值范围为.三、解答题(共5小题,满分74分)16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知=(1)求角A的大小;(2)若a=3,求b+c的最大值.17.如图,在三棱锥P﹣ABC中,BC⊥平面APC,AB=2,AP=PC=CB=2.(1)求证:AP⊥平面PBC;(2)求二面角P﹣AB﹣C的大小.18.已知a,b,c∈R,二次函数f(x)=ax2+bx+c,集合A={x|f(x)=ax+b},B={x|f(x)=cx+a}.(Ⅰ)若a=b=2c,求集合B;(Ⅱ)若A∪B={0,m,n}(m<n),求实数m,n的值.19.如图,椭圆E:+=1(a>b>0)左、右顶点为A,B,左、右焦点为F1,F2,|AB|=4,|F1F2|=2.直线y=kx+m(k>0)交椭圆E于C,D两点,与线段F1F2、椭圆短轴分别交于M,N两点(M,N不重合),且|CM|=|DN|.(Ⅰ)求椭圆E的方程;(Ⅱ)设直线AD,BC的斜率分别为k1,k2,求的取值范围.320.已知数列{an}满足:a1=a∈(0,1),且0<an+1≤an2﹣an3,设bn=(an﹣an+1)an+1(Ⅰ)比较a1﹣a2和的大小;(Ⅱ)求证:>an+1;(Ⅲ)设Tn为数列{bn}的前n项和,求证:Tn<.42015年浙江省绍兴市高考数学一模试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.若x∈R,则“x>1”,则“x2>1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件考点:必要条件、充分条件与充要条件的判断.专题:常规题型.分析:直接利用充要条件的判定判断方法判断即可.解答:解:因为“x>1”,则“x2>1”;但是“x2>1”不一定有“x>1”,所以“x>1”,是“x2>1”成立的充分不必要条件.故选A.点评:本题考查充要条件的判定方法的应用,考查计算能力.2.某快递公司快递一件物品的收费规定:物品不超过5千克,每件收费12元,超过5千克且不超过10千克,则超出部分每千克加收1.2元;…...