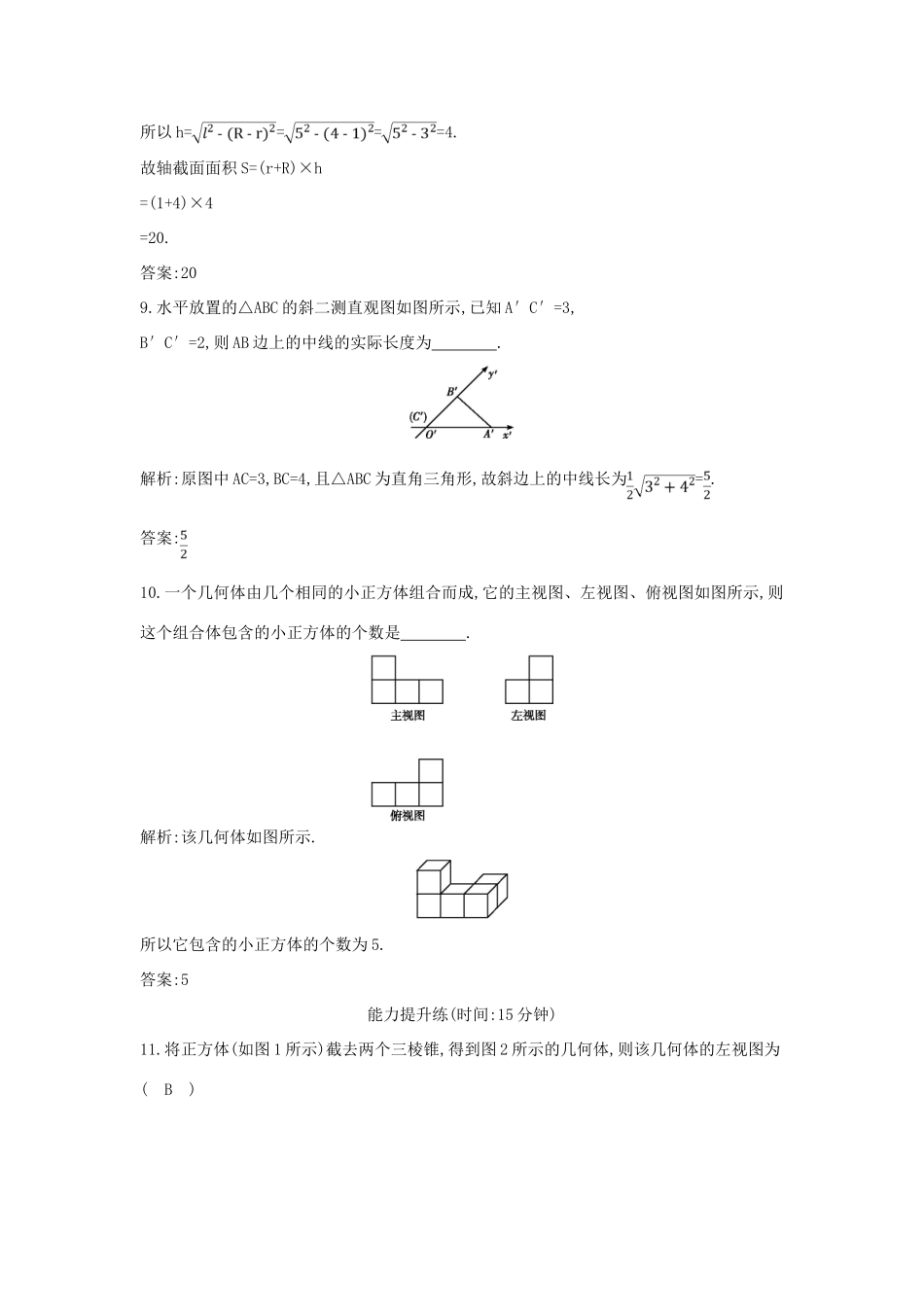
第七篇立体几何(必修2)第1节简单几何体、三视图和直观图【选题明细表】知识点、方法题号简单几何体结构特征1,2三视图的识别3,4,10,11,13,15与几何体相关的计算5,6,7,8,12,14,16直观图9基础对点练(时间:30分钟)1.观察如图的四个几何体,其中判断不正确的是(B)(A)①是棱柱(B)②不是棱锥(C)③不是棱锥(D)④是棱台解析:结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.2.如图所示几何体,是由哪个平面图形旋转得到的(A)解析:由旋转体的几何特征可知,旋转的平面图形为A中图形.故选A.3.如图所示的图形中,是正四棱锥的三视图的是(B)解析:由俯视图可排除A,C,D.故选B.4.如图为几何体的三视图,根据三视图可以判断这个几何体为(C)(A)圆锥(B)三棱锥(C)三棱柱(D)三棱台解析:由三视图可知,该几何体是一个横放的三棱柱.故选C.5.已知圆锥的底面面积为4π,高为2,则它的母线长为(C)(A)1(B)2(C)2(D)4解析:由题意知圆锥的底面半径r=2,高h=2.所以母线长l===2.6.已知球的半径为5,球心到截面的距离为3,则截面圆的面积为(D)(A)4π(B)6π(C)9π(D)16π解析:截面圆的半径为r==4,所以S=π·r2=16π.7.一个棱锥被平行底面的截面所截,若截面面积与底面面积之比为1∶2,则此棱锥的高被分成的两段之比为(D)(A)1∶(B)1∶4(C)(-1)∶(+1)(D)(+1)∶1解析:设截面上方小棱锥的高为h1,截面和底面间棱台的高为h2,则由棱锥的性质可得=()2,即()2=.所以=,故==+1.8.一个圆台的母线长为5,上、下底面直径分别为2,8,则圆台的轴截面面积为.解析:由题意r=1,R=4,l=5.所以h====4.故轴截面面积S=(r+R)×h=(1+4)×4=20.答案:209.水平放置的△ABC的斜二测直观图如图所示,已知A′C′=3,B′C′=2,则AB边上的中线的实际长度为.解析:原图中AC=3,BC=4,且△ABC为直角三角形,故斜边上的中线长为=.答案:10.一个几何体由几个相同的小正方体组合而成,它的主视图、左视图、俯视图如图所示,则这个组合体包含的小正方体的个数是.解析:该几何体如图所示.所以它包含的小正方体的个数为5.答案:5能力提升练(时间:15分钟)11.将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左视图为(B)解析:该几何体的左视图即为其在正方体的侧面BCC1B1上的正投影.故选B.12.正方体的内切球与外接球的半径之比为(C)(A)∶1(B)∶2(C)1∶(D)2∶解析:设正方体的内切球半径为r,外接球半径为R,则r=,R=a.所以r∶R=∶a=1∶.13.如图,在正方体ABCDA1B1C1D1中,M,N分别是BB1,BC的中点,则图中阴影部分在平面ADD1A1上的正投影为(A)解析:M,N两点在平面ADD1A1上的射影分别为AA1的中点,AD的中点.故选A.14.已知圆锥的轴截面面积为4cm2,底面面积为4πcm2,则其母线长为.解析:设圆锥底面半径为r,高为h,母线长为l.则由题意知解得所以母线长l==2(cm).答案:2cm15.把边长为的正方形ABCD沿对角线BD折起,连接AC,得到三棱锥CABD,其主视图、俯视图均为全等的等腰直角三角形(如图所示),则其左视图的面积为.解析:由两个视图可以得到三棱锥的直观图如图,AE⊥平面BCD,E为BD的中点,其左视图的面积即Rt△ACE的面积,由正方形的边长为得AE=CE=1,故左视图面积为.答案:16.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392cm2,母线与轴的夹角是45°,则这个圆台的高为.解析:圆台的轴截面如图所示,设圆台上、下底面半径分别为xcm,3xcm,延长AA1交OO1的延长线于S.在Rt△SOA中,∠ASO=45°,则∠SAO=45°,所以SO=AO=3x,所以OO1=2x.S轴截面=(6x+2x)·2x=392,解得x=7.故圆台的高OO1=14cm.答案:14cm精彩5分钟1.如图是由若干个相同的小立方体组成的几何体的俯视图,数字表示相应位置的小立方体的个数,则该几何体的左视图为(C)解题关键:能根据俯视图及相应位置正方体个数想像出几何体.解析:由俯视图知,左视图从左到右能看到的小立方体个数分别为2,3,1.故选C.2.如图,矩形O′A′B′C′是水平放置的平面图形OABC的直观图,其中O′A′=6,O′C′=2,则原图形OABC的面积为.解题关键:注意已知图形为平面的直观图,要逆用斜二测画法确定原图形的长度和高度.解析:由题意知原图形OABC是平行四边形,且OA=BC=6,设平行四边形OABC的高为OE,则OE××=O′C′=2,所以OE=4,所以SOABC▱=6×4=24.答案:243.若长方体的三个面的面积分别为6,12,18,则长方体的对角线长为.解题关键:利用方程的思想求解.解析:设长方体的长、宽、高分别为x,y,z,则由题意知①×②×③得(xyz)2=6×12×18,所以xyz=36,把①②③代入解得所以长方体的对角线l===7.答案:7