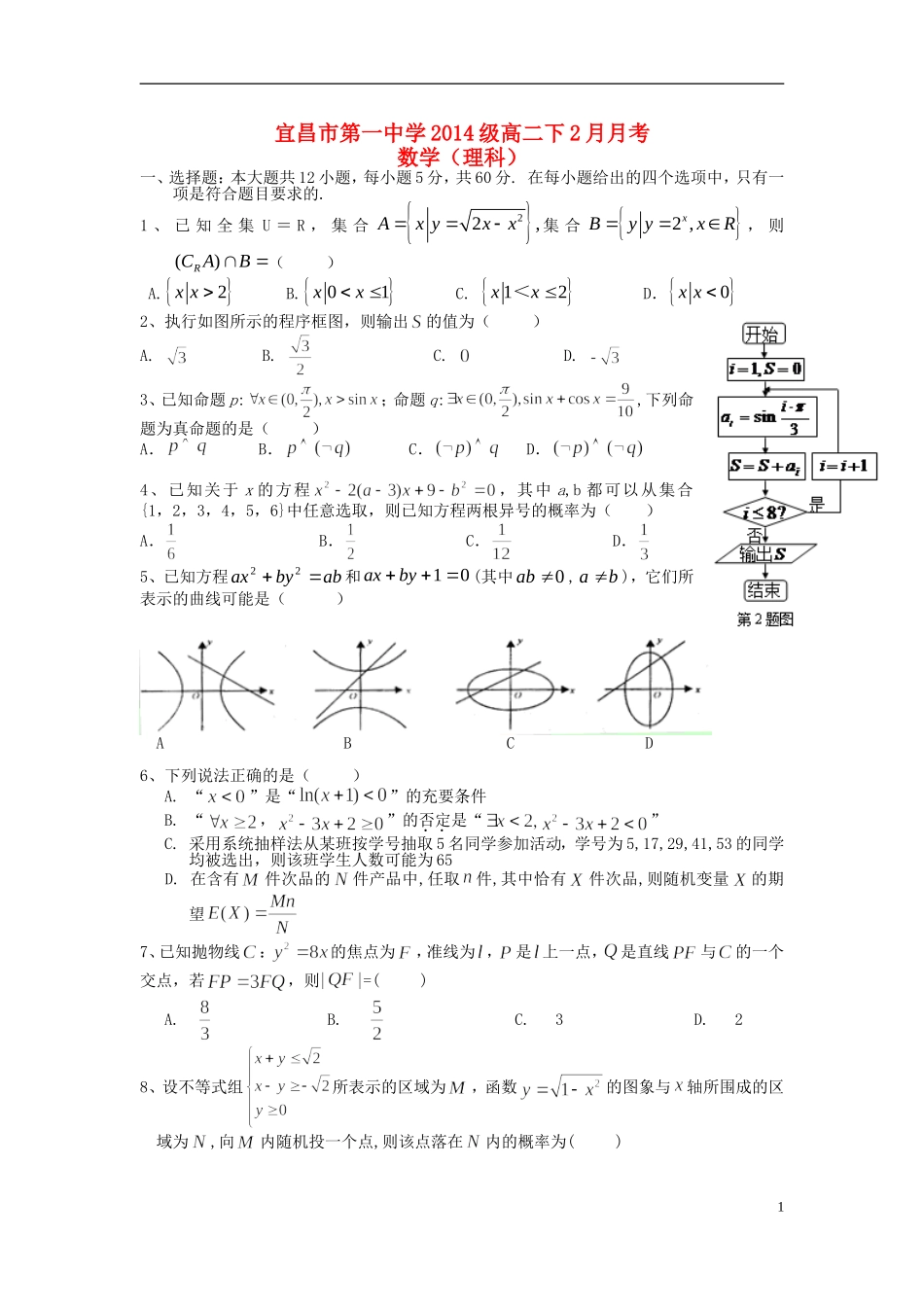
宜昌市第一中学2014级高二下2月月考数学(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知全集U=R,集合22,Axyxx集合2,xByyxR,则()RCAB()A.2xxB.01xxC.12xx<D.0xx2、执行如图所示的程序框图,则输出的值为()A.B.C.D.3、已知命题p:;命题q:,下列命题为真命题的是()A.B.C.D.4、已知关于x的方程,其中a,b都可以从集合{1,2,3,4,5,6}中任意选取,则已知方程两根异号的概率为()A.B.C.D.5、已知方程abbyax22和01byax(其中0ab,ba),它们所表示的曲线可能是()ABCD6、下列说法正确的是()A.“”是“”的充要条件B.“,”的否定是“”C.采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,17,29,41,53的同学均被选出,则该班学生人数可能为65D.在含有件次品的件产品中,任取件,其中恰有件次品,则随机变量的期望7、已知抛物线:的焦点为,准线为,是上一点,是直线与的一个交点,若,则=()A.B.C.3D.28、设不等式组所表示的区域为,函数的图象与轴所围成的区域为,向内随机投一个点,则该点落在内的概率为()1A.B.C.D.9、如图,空间四边形中,,,,点在线段上,且,点为的中点,则()A.B.C.D.10、用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有()个A.180B.216C.324D.38411、给定圆:及抛物线:,过圆心作直线,此直线与上述两曲线的四个交点,自上而下顺次记为,如果线段的长按此顺序构成一个等差数列,则直线的斜率为()A.B.C.D.12、如图,在等腰梯形中,,且,。以为焦点,且过点的双曲线的离心率;以为焦点,且过点的双曲线的离心率,则的取值范围为()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分.将答案填在答题纸上.13、已知二项式的展开式的二项式系数之和为,则展开式中含项的系数是__.14、已知直线过点,若可行域的外接圆直径为20,则n=_.15、已知椭圆的右焦点为,设为椭圆上关于原点对称的两点,的中点为,的中点为,原点在以线段为直径的圆上。若直线的斜率满足,则椭圆离心率的取值范围为.16、如图,直线l⊥平面,垂足为O,已知在直角三角形ABC中,BC=1,AC=2,AB=5.该直角三角形在空间做符合以下条件的自由运动:(1)Al,(2)C.则B、O两点间的最大距离为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17、已知命题:存在实数使函数在区间上的最小值等于2;命题:存在实数,使函数f(x)=loga(2-ax)在[0,1]上是关于x的减函数.若“为假”且“为真”,试求实数的取值范围.218、某班从6名班干部(其中男生4人,女生2人)中,任选3人参加学校的义务劳动.(1)设所选3人中女生人数为X,求X的分布列;(2)求男生甲或女生乙被选中的概率;(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B|A).19、如图,在平面直角坐标系中,点A(0,3),直线:。设圆的半径为1,圆心在上。(1)若圆心也在直线上,过点作圆的切线,求切线的方程;(2)若圆上存在点,使,求圆心的横坐标的取值范围.20、根据最新修订的《环境空气质量标准》指出空气质量指数在,各类人群可正常活动.宜昌市环保局在2015年对本市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为0,10,10,20,20,30,30,40,40,50,由此得到样本的空气质量指数频率分布直方图,如图.(1)求a的值;并根据样本数据,试估计这一年度的空气质量指数的平均值;(2)用这50个样本数据来估计全年的总体数据,将频率视为概率.如果空气质量指数不超过20,就认定空气质量为“最优等级”.从这一年的监测数据中随机抽取2天的数值,其中达到“最优等级”的天数为,求的分布列,并估计一个月(30天)中空气质量能达到“最优等级”的天数.21、如图,四棱锥中,,,,为等边三角形.3第20题图(1)证明:;(2)求二面角的平面角...