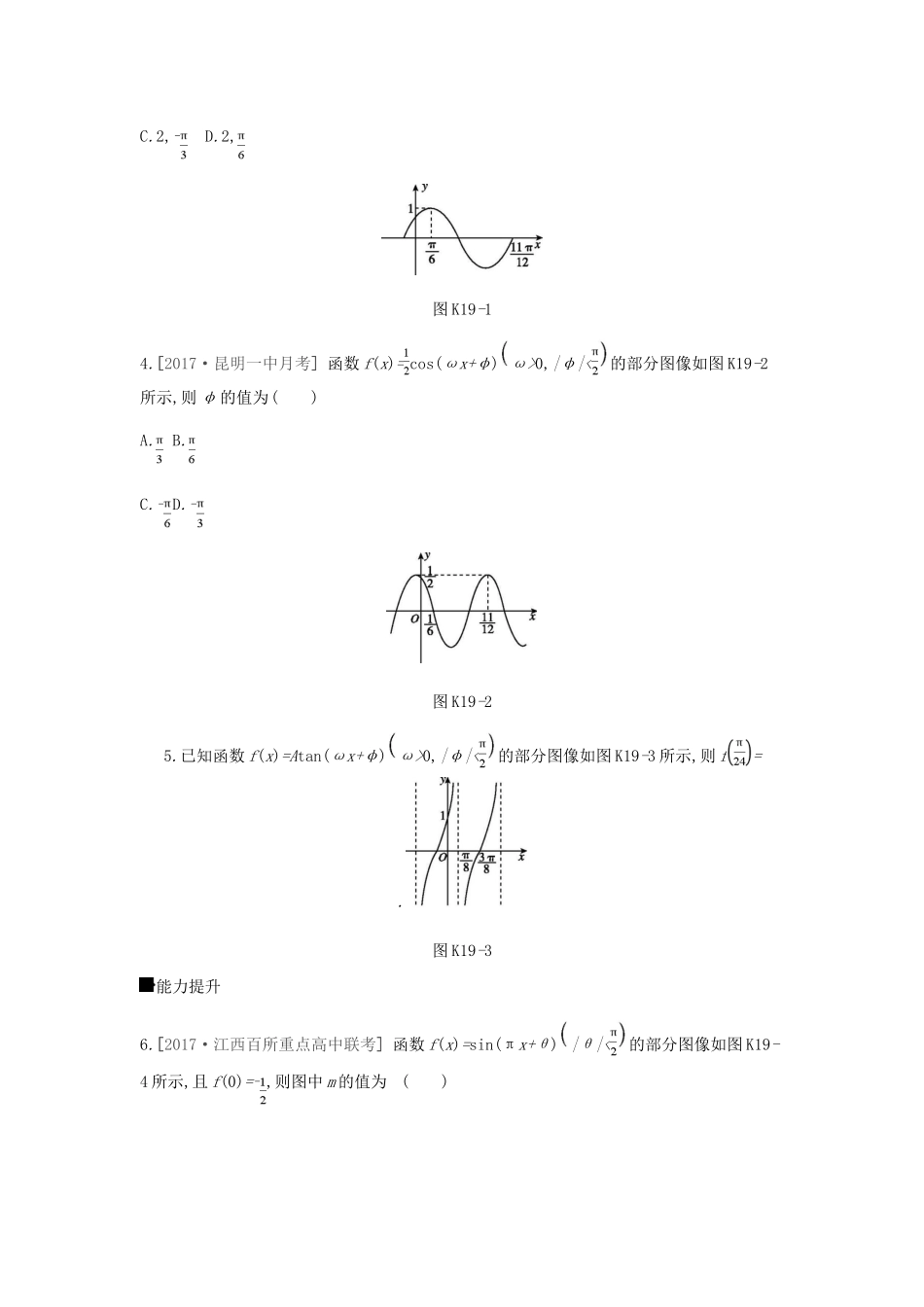
作业(十九)第19讲函数y=Asin(ωx+φ)的图像及三角函数模型的简单应用基础热身1.[2017·东莞四校联考]为了得到函数y=sin2x-的图像,可以将函数y=sin2x的图像()A.向右平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向左平移个单位长度2.[2017·郴州三模]函数f(x)=2sin2x-的图像关于直线x=x0对称,则|x0|的最小值为()A.B.C.D.3.[2017·榆林三模]函数f(x)=Asin(ωx+φ)A>0,ω>0,|φ|<的部分图像如图K19-1所示,则ω,φ的值分别为()A.2,0B.2,C.2,-D.2,图K19-14.[2017·昆明一中月考]函数f(x)=cos(ωx+φ)ω>0,|φ|<的部分图像如图K19-2所示,则φ的值为()A.B.C.-D.-图K19-25.已知函数f(x)=Atan(ωx+φ)ω>0,|φ|<的部分图像如图K19-3所示,则f=.图K19-3能力提升6.[2017·江西百所重点高中联考]函数f(x)=sin(πx+θ)|θ|<的部分图像如图K19-4所示,且f(0)=-,则图中m的值为()图K19-4A.1B.C.2D.或27.[2017·绵阳三诊]已知函数f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,A(a,0),B(b,0)是其图像上两点,若|a-b|的最小值是1,则f=()A.2B.-2C.D.-8.[2017·辽南协作体三模]已知函数f(x)=Asin(ωx+φ)A>0,|φ|<的图像在y轴左侧的第一个最高点为-,3,第一个最低点为-,m,则函数f(x)的解析式为()A.f(x)=3sinB.f(x)=3sinC.f(x)=3sinD.f(x)=3sin9.[2017·泉州二模]已知曲线C:y=sin(2x+φ)|φ|<的一条对称轴方程为x=,曲线C向左平移θ(θ>0)个单位长度,得到的曲线E的一个对称中心为,0,则|φ-θ|的最小值是()A.B.C.D.10.[2017·成都九校联考]已知函数f(x)=Asin(2x+φ)-A>0,0<φ<的图像在y轴上的截距为1,且关于直线x=对称,若对于任意的x∈0,,都有m2-3m≤f(x),则实数m的取值范围为()A.B.[1,2]C.D.11.某实验室一天的温度(单位:摄氏度)随时刻t(单位:时)的变化近似满足函数关系:f(t)=10-·cost-sint,t∈[0,24),则该实验室这一天的最大温差是.12.[2017·柳州、钦州一模]将函数f(x)=3sin4x+图像上所有点的横坐标伸长到原来的2倍,再向右平移个单位长度,得到函数y=g(x)的图像,则y=g(x)的解析式为.13.(15分)[2017·衡阳十校联考]已知函数f(x)=sin2x++sin2x.(1)求函数f(x)的最小正周期;(2)若函数g(x)对任意x∈R,有g(x)=fx+,求函数g(x)在-,上的值域.14.(15分)[2017·台州质量评估]已知函数f(x)=sin(ωx+φ)ω>0,|φ|≤的最小正周期为π,且x=为f(x)图像的一条对称轴.(1)求ω和φ的值;(2)设函数g(x)=f(x)+fx-,求g(x)的单调递减区间.难点突破15.(5分)将函数f(x)=3sin2x+的图像向左平移个单位长度,再向上平移1个单位长度,得到g(x)的图像,若g(x1)g(x2)=16,且x1,x2∈-,,则2x1-x2的最大值为()A.B.C.D.16.(5分)[2017·芜湖质检]将函数f(x)=sinωx(ω>0)的图像向左平移个单位长度得到函数g(x)的图像,若函数g(x)的图像关于直线x=ω对称且在区间(-ω,ω)内单调递增,则ω的值为()A.B.C.D.课时作业(十九)1.B[解析]y=sin2x-=sin2x-,故将函数y=sin2x的图像向右平移个单位长度,可得y=sin2x-的图像.2.A[解析]函数f(x)=2sin2x-,由2x-=+kπ(k∈Z),可得x=kπ+(k∈Z),则x0=kπ+(k∈Z),当k=-1时,|x0|取到最小值.3.D[解析]由函数的图像可知A=1,=-=,所以T=π,所以ω=2,又函数的图像经过点,1,所以1=sin2×+φ,因为|φ|<,所以φ=.4.B[解析]由题意可得=-=,∴T=1=,解得ω=2π,∴f(x)=cos(2πx+φ). 点,0在函数图像上,∴0=cos2π×+φ,∴2π×+φ=kπ+,k∈Z,解得φ=kπ+,k∈Z, |φ|<,∴当k=0时,φ=.5.[解析]由图像知=2×-=,所以ω=2.因为2×+φ=kπ+(k∈Z),所以φ=kπ+(k∈Z),又|φ|<,所以φ=.这时f(x)=Atan2x+.又函数图像过点(0,1),代入上式得A=1,所以f(x)=tan2x+.所以f=tan2×+=.6.B[解析] f(0)=-,∴sinθ=-,又|θ|<,∴θ=-.由πx-=2kπ+(k∈Z),得x=2k+(k∈Z),结合图像得=,∴m=.7.B[解析] 函数f(x)=4cos(ωx+φ)(ω>0,0<φ<π)为奇函数,∴φ=,f(x)=-4sinωx. A(a,0),B(b,0)是其图像上两点,|a-b|的最小值是1,∴×=1,∴ω=π,f(x)=-4sinπx,则f=-4sin=-2.8.A[解析]因为函数f(x)=Asin(ωx+φ)A>0,|φ|<的图像在y轴左侧的第一个最高点为-,3,第-个最低点为-,m,所以T=2×-+=π=.由题意知ω<0,所以ω=-2,并且A=3.又f-=3,即sin-2×+φ=1,且|φ|<,所...