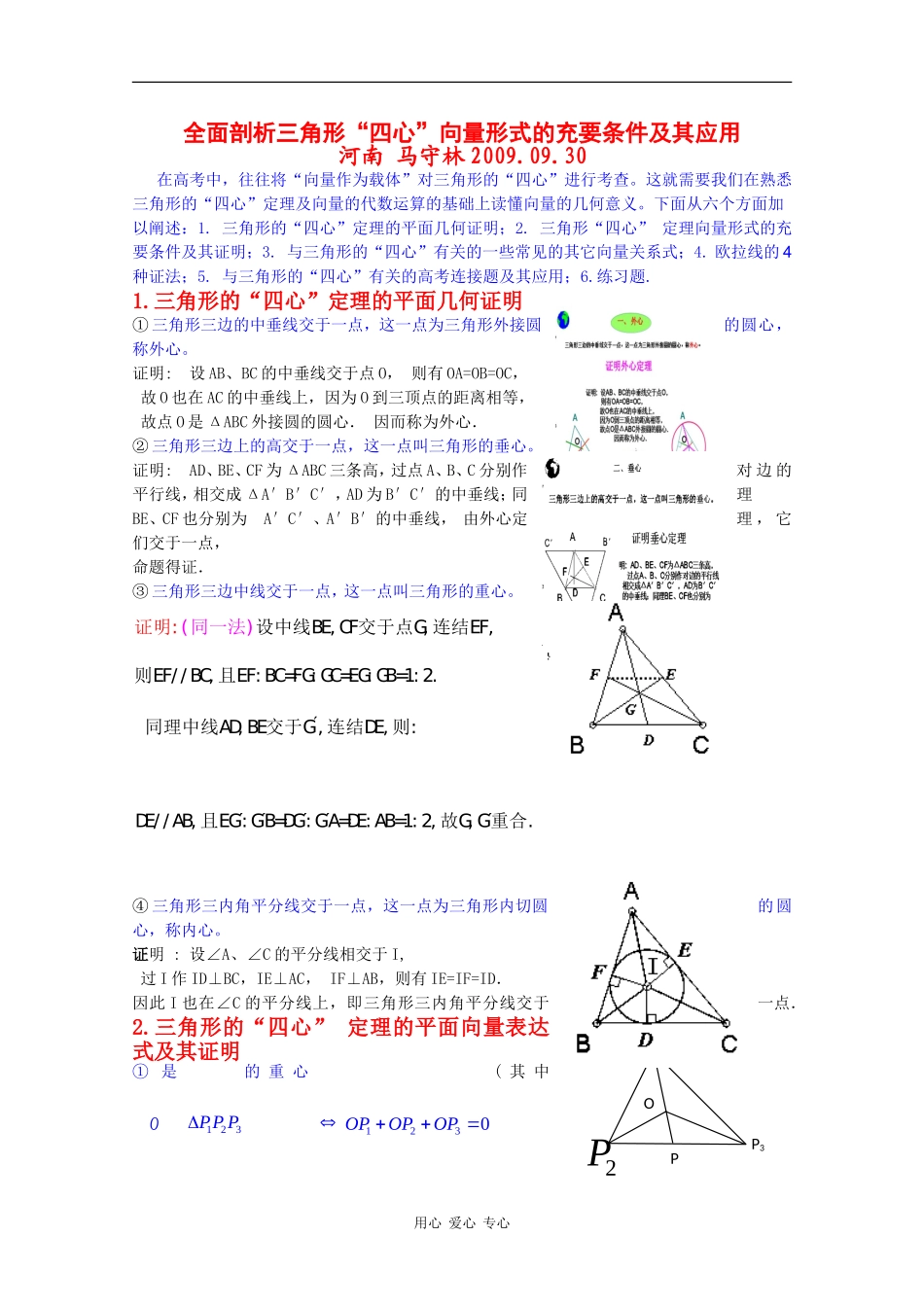
全面剖析三角形“四心”向量形式的充要条件及其应用河南马守林2009.09.30在高考中,往往将“向量作为载体”对三角形的“四心”进行考查。这就需要我们在熟悉三角形的“四心”定理及向量的代数运算的基础上读懂向量的几何意义。下面从六个方面加以阐述:1.三角形的“四心”定理的平面几何证明;2.三角形“四心”定理向量形式的充要条件及其证明;3.与三角形的“四心”有关的一些常见的其它向量关系式;4.欧拉线的4种证法;5.与三角形的“四心”有关的高考连接题及其应用;6.练习题.1.三角形的“四心”定理的平面几何证明①三角形三边的中垂线交于一点,这一点为三角形外接圆的圆心,称外心。证明:设AB、BC的中垂线交于点O,则有OA=OB=OC,故O也在AC的中垂线上,因为O到三顶点的距离相等,故点O是ΔABC外接圆的圆心.因而称为外心.②三角形三边上的高交于一点,这一点叫三角形的垂心。证明:AD、BE、CF为ΔABC三条高,过点A、B、C分别作对边的平行线,相交成ΔA′B′C′,AD为B′C′的中垂线;同理BE、CF也分别为A′C′、A′B′的中垂线,由外心定理,它们交于一点,命题得证.③三角形三边中线交于一点,这一点叫三角形的重心。设中线BE,CF交于点(G证明,连同一法):结EF,则EF//BC,且EF:BC=FG:GC=EG:GB=1:2.同理中线AD,BE交于G,连结DE,则:DE//AB,且EG:GB=DG:GA=DE:AB=1:2,故G,G重合.④三角形三内角平分线交于一点,这一点为三角形内切圆的圆心,称内心。证明:设∠A、∠C的平分线相交于I,过I作ID⊥BC,IE⊥AC,IF⊥AB,则有IE=IF=ID.因此I也在∠C的平分线上,即三角形三内角平分线交于一点.2.三角形的“四心”定理的平面向量表达式及其证明①O是123PPP的重心1230OPOPOP�(其中用心爱心专心P12PP3OP,,abc是123PPP三边)证明:充分性1230OPOPOP�O是123PPP的重心若1230OPOPOP�,则123OPOPOP�,以1OP�,2OP�为邻边作平行四边形132'OPPP,设3OP与12PP交于点3P,则3P为12PP的中点,有'123OPOPOP��,得'33OPOP�,即'33,,,OPPP四点共线,故3PP为123PPP的中线,同理,12,POPO亦为123PPP的中线,所以,O为的重心。必要性:O是123PPP的重心1230OPOPOP�如图,延长1PO交23PP于P,则P为23PP的中点,由重心的性质得12POOP�. 12323122()2�OPOPOPOPOPOP∴1230OPOPOP�②点O是123PPP的垂心122331OPOPOPOPOPOP�证明:O是123PPP的垂心312OPPP�,123OPPP�31232132310()0OPPPOPOPOPOPOPOPOP�同理123OPPP�3112OPOPOPOP�故当且仅当122331OPOPOPOPOPOP�.③点O是123PPP的外心23OPOPOP�.证明:O是△ABC的外心|OA�|=|OB�|=|OC�|(或OA�2=OB�2=OC�2)(点O到三边距离相等)(OA�+OB�)·AB�=(OB�+OC�)·BC�=(OC�+OA�)·CA�=0(O为三边垂直平分线的交点)④O是123PPP的内心1230aOPbOPcOP�。(其中,,abc用心爱心专心P12PP3OPABCDO是123PPP三边)证明:充分性:1230�aOPbOPcOPO是123PPP的内心1231112113()()aOPbOPcOPaOPbOPPPcOPPP�=11213()0�abcOPbPPcPP所以13121()PPPPbcPOabccb���,而12PPc�,13PPb�分别是12PP�,13PP�方向上的单位向量,所以向量1312PPPPcb��平分213PPP,即1PO�平分213PPP,同理2PO�平分123PPP,得到点O是123PPP的内心。必要性:O是123PPP的内心1230�aOPbOPcOP若点O为123PPP的内心,延长1PO交23PP于P,由三角形内角平分线的性质定理,有1311223PPPOPPbcOPPPPPa,于是1()0�aOPbcOP再由23PPcPPb,有23bcOPOPOPbcbc�(定比分点)代入前式中便得1230aOPbOPcOP�.必要性证法二:设O是ABC内任一点,以O为坐标原点,OA所在直线为x轴,建立直角坐标系。并设AOC,AOB).sinr,cosr(C),sinq,cosq(B),0,p(A其中显然OC,OB不共线,由平面向量基本定理,可设),Ry,x(OCyOBxOA则用心爱心...