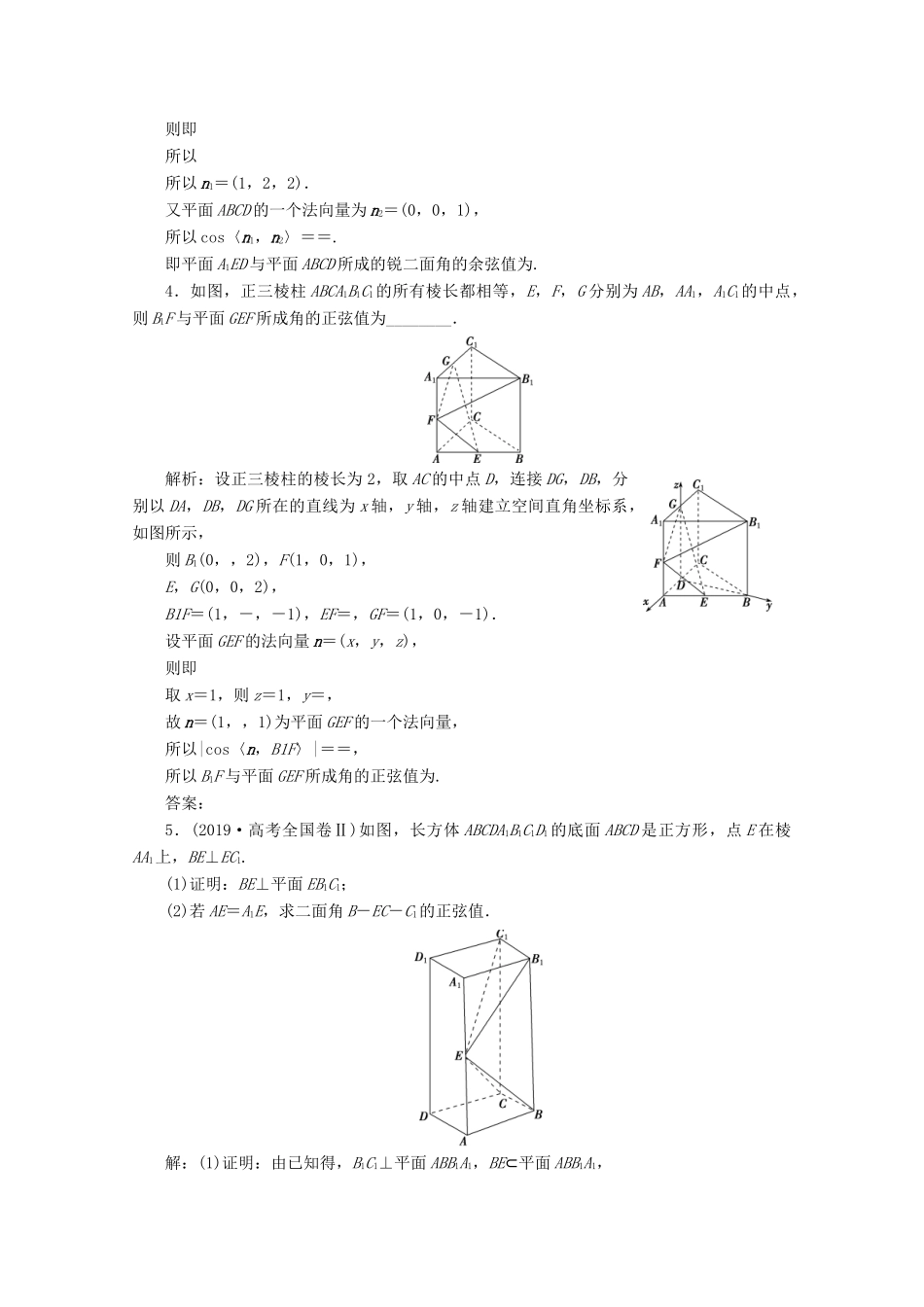
第7讲立体几何中的向量方法[基础题组练]1.将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,AC长为,A1B1长为,其中B1与C在平面AA1O1O的同侧.则异面直线B1C与AA1所成的角的大小为()A.B.C.D.解析:选B.以O为坐标原点建系如图,则A(0,1,0),A1(0,1,1),B1,C.所以AA1=(0,0,1),B1C=(0,-1,-1),所以cos〈AA1,B1C〉===-,所以〈AA1,B1C〉=,所以异面直线B1C与AA1所成的角为.故选B.2.如图,已知长方体ABCDA1B1C1D1中,AD=AA1=1,AB=3,E为线段AB上一点,且AE=AB,则DC1与平面D1EC所成的角的正弦值为()A.B.C.D.解析:选A.如图,以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则C1(0,3,1),D1(0,0,1),E(1,1,0),C(0,3,0),所以DC1=(0,3,1),D1E=(1,1,-1),D1C=(0,3,-1).设平面D1EC的法向量为n=(x,y,z),则即即取y=1,得n=(2,1,3).因为cos〈DC1,n〉===,所以DC1与平面D1EC所成的角的正弦值为,故选A.3.在正方体ABCDA1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为()A.B.C.D.解析:选B.以A为原点建立如图所示的空间直角坐标系Axyz,设棱长为1,则A1(0,0,1),E,D(0,1,0),所以A1D=(0,1,-1),A1E=,设平面A1ED的一个法向量为n1=(1,y,z),则即所以所以n1=(1,2,2).又平面ABCD的一个法向量为n2=(0,0,1),所以cos〈n1,n2〉==.即平面A1ED与平面ABCD所成的锐二面角的余弦值为.4.如图,正三棱柱ABCA1B1C1的所有棱长都相等,E,F,G分别为AB,AA1,A1C1的中点,则B1F与平面GEF所成角的正弦值为________.解析:设正三棱柱的棱长为2,取AC的中点D,连接DG,DB,分别以DA,DB,DG所在的直线为x轴,y轴,z轴建立空间直角坐标系,如图所示,则B1(0,,2),F(1,0,1),E,G(0,0,2),B1F=(1,-,-1),EF=,GF=(1,0,-1).设平面GEF的法向量n=(x,y,z),则即取x=1,则z=1,y=,故n=(1,,1)为平面GEF的一个法向量,所以|cos〈n,B1F〉|==,所以B1F与平面GEF所成角的正弦值为.答案:5.(2019·高考全国卷Ⅱ)如图,长方体ABCDA1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B-EC-C1的正弦值.解:(1)证明:由已知得,B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,所以BE⊥平面EB1C1.(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故AE=AB,AA1=2AB.以D为坐标原点,DA的方向为x轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).设平面EBC的法向量为n=(x,y,z),则即所以可取n=(0,-1,-1).设平面ECC1的法向量为m=(x1,y1,z1),则即所以可取m=(1,1,0).于是cosn,m==-.所以,二面角B-EC-C1的正弦值为.6.(2019·福州市质量检测)如图,四棱锥PABCD,AB∥CD,∠BCD=90°,AB=2BC=2CD=4,△PAB为等边三角形,平面PAB⊥平面ABCD,Q为PB的中点.(1)求证:AQ⊥平面PBC;(2)求二面角BPCD的余弦值.解:(1)证明:因为AB∥CD,∠BCD=90°,所以AB⊥BC,又平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,所以BC⊥平面PAB,又AQ⊂平面PAB,所以BC⊥AQ,因为Q为PB的中点,且△PAB为等边三角形,所以PB⊥AQ,又PB∩BC=B,所以AQ⊥平面PBC.(2)取AB的中点O,连接PO,OD,因为△PAB为等边三角形,所以PO⊥AB,由平面PAB⊥平面ABCD,PO⊂平面PAB,得PO⊥平面ABCD,所以PO⊥OD,由AB=2BC=2CD=4,∠ABC=90°,可知OD∥BC,所以OD⊥AB.以AB中点O为坐标原点,分别以OD,OB,OP所在直线为x,y,z轴,建立如图所示的空间直角坐标系Oxyz,则A(0,-2,0),D(2,0,0),C(2,2,0),P(0,0,2),B(0,2,0),所以AD=(2,2,0),DP=(-2,0,2),CD=(0,-2,0).因为Q为PB的中点,所以Q(0,1,),由(1)知,平面PBC的一个法向量为AQ=(0,3,).设平面PCD的法向量为n=(x,y,z),由,得,取z=1,则n=...