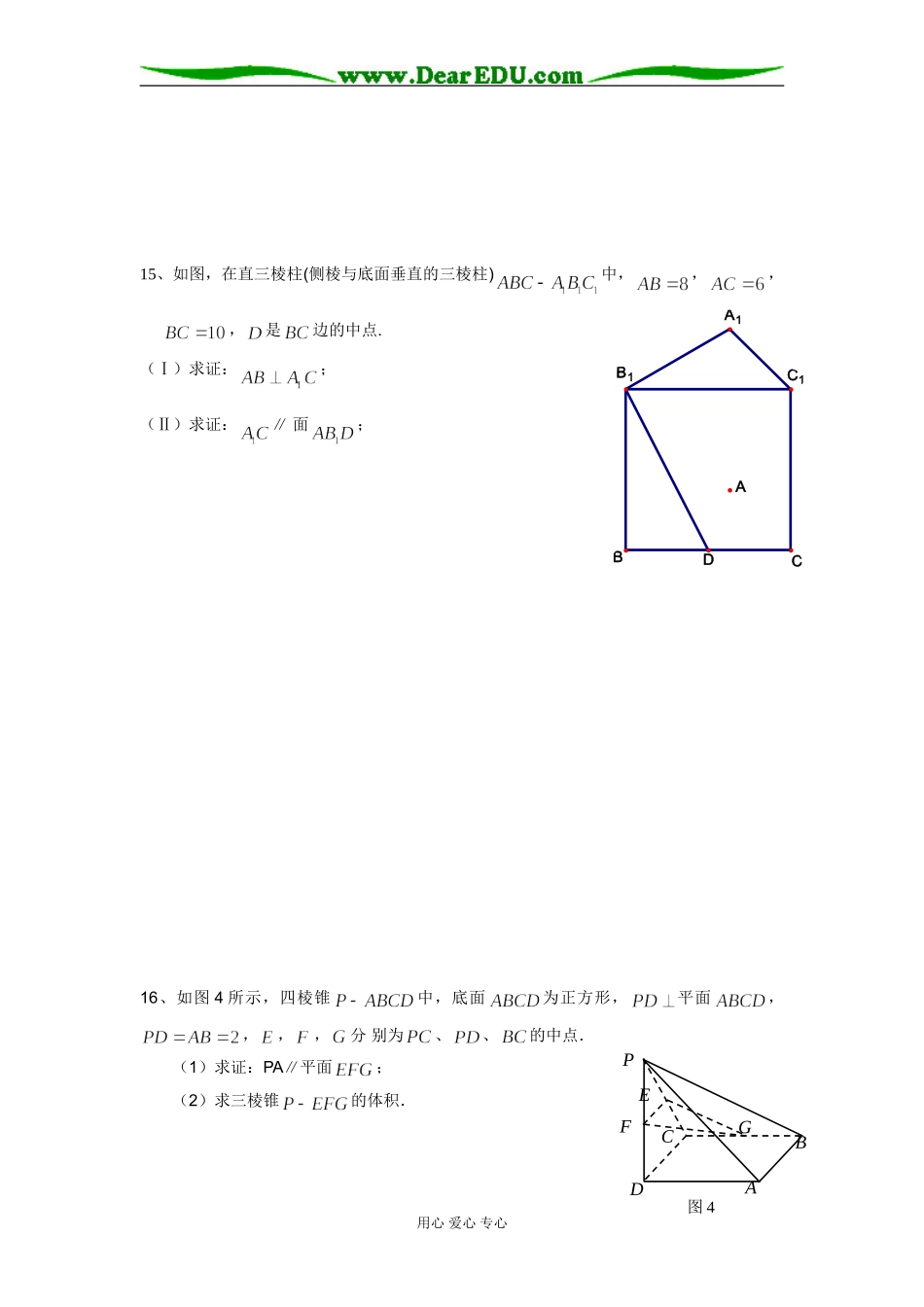
PPPPQQQQRRRRSSSSPPPPQQQQRRRRSSSSPPPPQQQQRRRRSSSS直线与平面、平面与平面平行一、选择题:1、正方体中,与面的对角线异面的棱有()A.4条B.6条C.8条D.10条2、下列各图是正方体或正四面体,P,Q,R,S分别是所在棱的中点,这四个点中不共面的一个图是()ABCD3、下列命题中,正确的是()A.经过不同的三点有且只有一个平面B.分别在两个平面内的两条直线一定是异面直线C.垂直于同一个平面的两条直线是平行直线D.垂直于同一个平面的两个平面平行4、对于不重合的两直线m、n和平面,下列命题中的真命题是()A.如果是异面直线,那行n//aB.如果共面,那么m//nC.如果是异面直线,那么n与a相交D.如果共面,那么m//n5、已知a,b是两条不重合的直线,α,β,γ是三个两两不重合的平面,给出下列四个命题:①若a⊥α,a⊥β,则②若③若④若其中正确命题的序号是()A.①②B.①③C.③④D.①④6、给出下列关于互不相同的直线m、l、n和平面α、β的四个命题:①若;②若m、l是异面直线,;③若;④若其中为假命题的是()A.①B.②C.③D.④7、对于不重合的两个平面,给定下列条件:①存在平面,使得α、β都垂直于;②存在平面,使得α、β都平行于;③存在直线,直线,使得;④存在异面直线l、m,使得其中,可以判定α与β平行的条件有()A.1个B.2个C.3个D.4个用心爱心专心8、已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是()A.平面ABC必平行于αB.平面ABC必与α相交C.平面ABC必不垂直于αD.存在△ABC的一条中位线平行于α或在α内9、若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的()(A)充分非必要条件;(B)必要非充分条件;(C)充要条件;(D)非充分非必要条件10、如图,正三棱柱的各棱长都2,E,F分别是的中点,则EF的长是()(A)2(B)(C)(D)二、填空题:11、设平面α∥β,A、C∈α,B、D∈β,直线AB与CD交于S,若AS=18,BS=9,CD=34,则CS=___________.12、已知a、b为不垂直的异面直线,α是一个平面,则a、b在α上的射影有可能是①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点.在上面结论中,正确结论的编号是__________.(写出所有正确结论的编号)13、在正方体ABCD—A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则①四边形BFD′E一定是平行四边形.②四边形BFD′E有可能是正方形.③四边形BFD′E在底面ABCD内的投影一定是正方形.④平面BFD′E有可能垂直于平面BB′D.以上结论正确的为.(写出所有正确结论的编号)三、解答题:14、如下图,正方体ABCD—A1B1C1D1中,侧面对角线AB1、BC1上分别有两点E、F,且B1E=C1F。求证:EF∥平面ABCD。用心爱心专心A1B1C1GFEABCDC1B1A1CBA15、如图,在直三棱柱(侧棱与底面垂直的三棱柱)中,,,,是边的中点.(Ⅰ)求证:;(Ⅱ)求证:∥面;16、如图4所示,四棱锥中,底面为正方形,平面,,,,分别为、、的中点.(1)求证:PA∥平面;(2)求三棱锥的体积.用心爱心专心图4ABCDEFGP17、如图,在多面体ABCDE中,AE⊥ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F在CD上(不含C,D两点)(1)求多面体ABCDE的体积;(2)若F为CD中点,求证:EF⊥面BCD;(3)当的值=时,能使AC∥平面EFB,并给出证明。直线与平面、平面与平面平行参考答案一、选择题:BDCBDCBDAC二、填空体:11、或6812、__①②④_______13、①③④三、解答题14、证法一:分别过E、F作EM⊥AB于点M,FN⊥BC于点N,连结MN新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆 BB1⊥平面ABCD,∴BB1⊥AB,BB1⊥BC新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆用心爱心专心ABCEDFEDC1B1A1CBAHABCDEFGP∴EM∥BB1,FN∥BB1新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆∴...