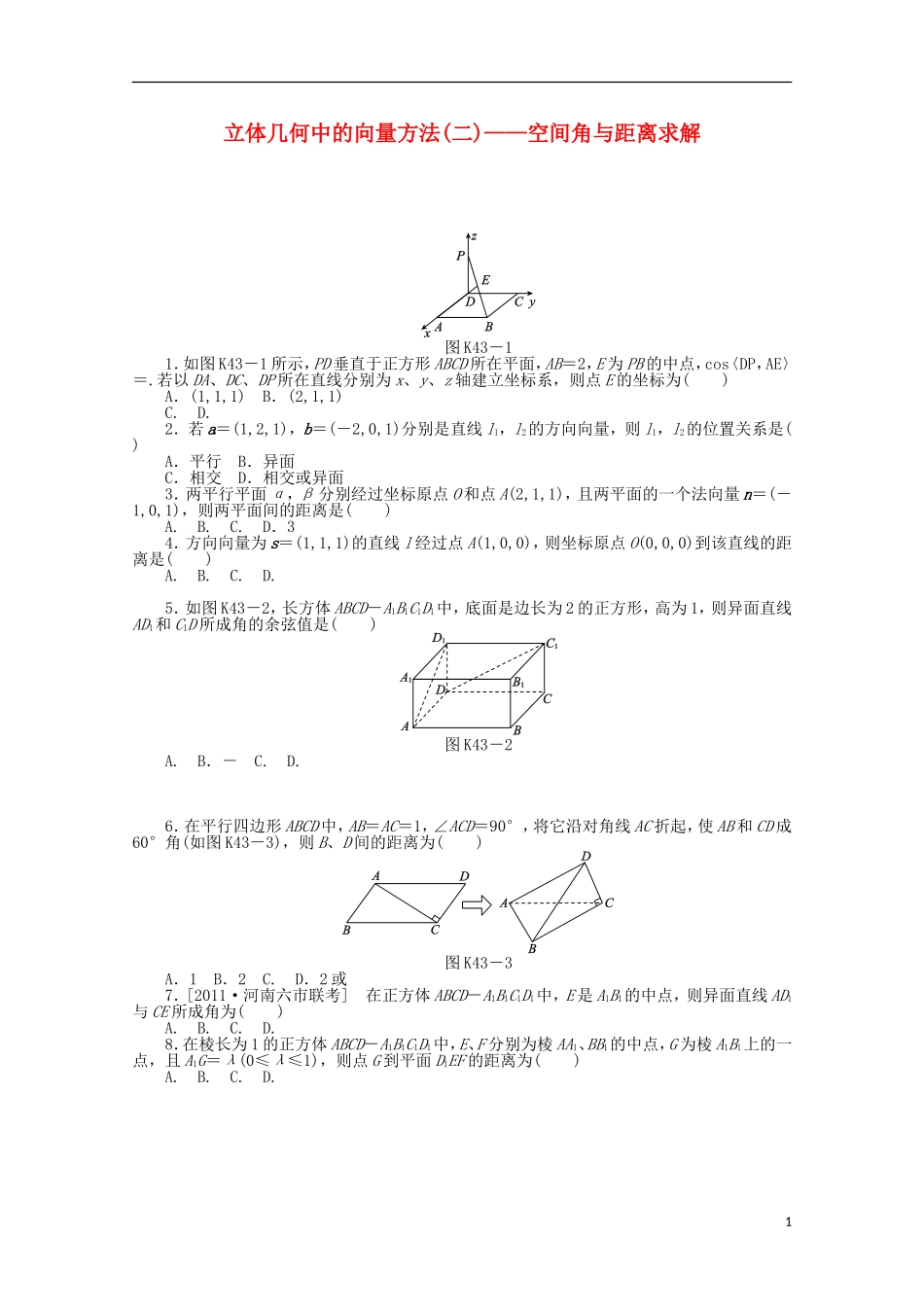
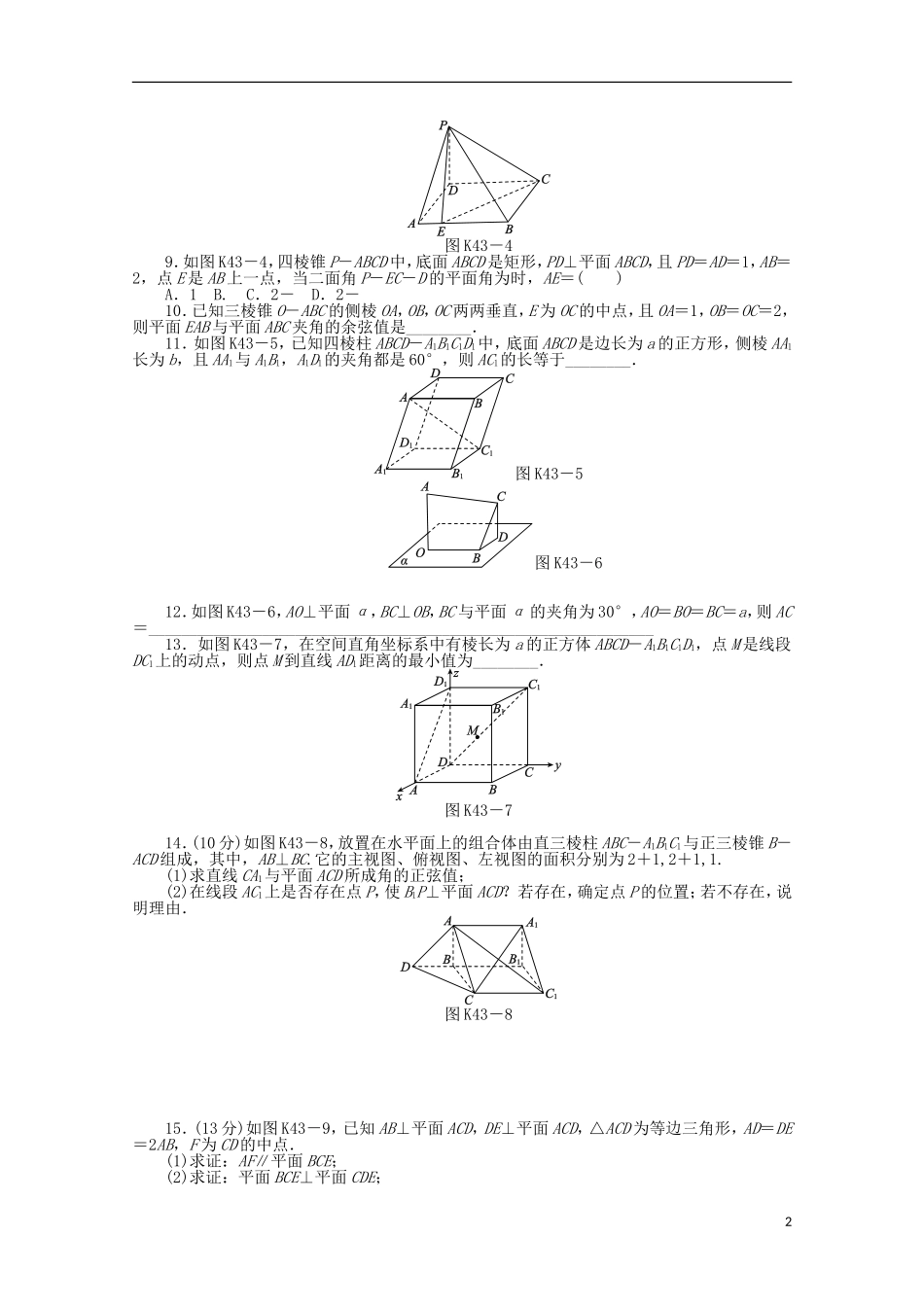
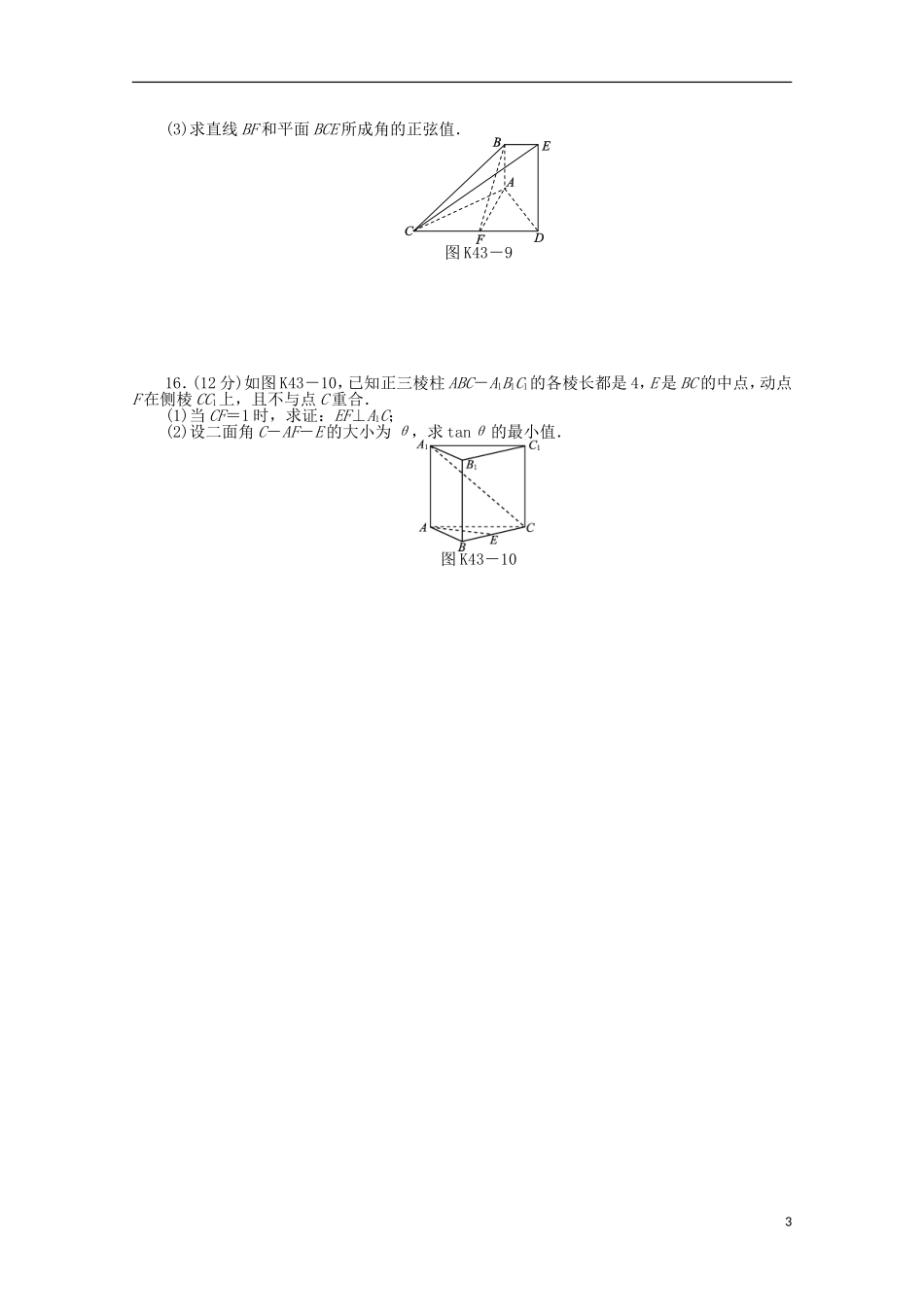
立体几何中的向量方法(二)——空间角与距离求解图K43-11.如图K43-1所示,PD垂直于正方形ABCD所在平面,AB=2,E为PB的中点,cos〈DP,AE〉=.若以DA、DC、DP所在直线分别为x、y、z轴建立坐标系,则点E的坐标为()A.(1,1,1)B.(2,1,1)C.D.2.若a=(1,2,1),b=(-2,0,1)分别是直线l1,l2的方向向量,则l1,l2的位置关系是()A.平行B.异面C.相交D.相交或异面3.两平行平面α,β分别经过坐标原点O和点A(2,1,1),且两平面的一个法向量n=(-1,0,1),则两平面间的距离是()A.B.C.D.34.方向向量为s=(1,1,1)的直线l经过点A(1,0,0),则坐标原点O(0,0,0)到该直线的距离是()A.B.C.D.5.如图K43-2,长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和C1D所成角的余弦值是()图K43-2A.B.-C.D.6.在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB和CD成60°角(如图K43-3),则B、D间的距离为()图K43-3A.1B.2C.D.2或7.[2011·河南六市联考]在正方体ABCD-A1B1C1D1中,E是A1B1的中点,则异面直线AD1与CE所成角为()A.B.C.D.8.在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱AA1、BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为()A.B.C.D.1图K43-49.如图K43-4,四棱锥P-ABCD中,底面ABCD是矩形,PD⊥平面ABCD,且PD=AD=1,AB=2,点E是AB上一点,当二面角P-EC-D的平面角为时,AE=()A.1B.C.2-D.2-10.已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,E为OC的中点,且OA=1,OB=OC=2,则平面EAB与平面ABC夹角的余弦值是________.11.如图K43-5,已知四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的正方形,侧棱AA1长为b,且AA1与A1B1,A1D1的夹角都是60°,则AC1的长等于________.图K43-5图K43-612.如图K43-6,AO⊥平面α,BC⊥OB,BC与平面α的夹角为30°,AO=BO=BC=a,则AC=______________________________________________________________13.如图K43-7,在空间直角坐标系中有棱长为a的正方体ABCD-A1B1C1D1,点M是线段DC1上的动点,则点M到直线AD1距离的最小值为________.图K43-714.(10分)如图K43-8,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC.它的主视图、俯视图、左视图的面积分别为2+1,2+1,1.(1)求直线CA1与平面ACD所成角的正弦值;(2)在线段AC1上是否存在点P,使B1P⊥平面ACD?若存在,确定点P的位置;若不存在,说明理由.图K43-815.(13分)如图K43-9,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求证:平面BCE⊥平面CDE;2(3)求直线BF和平面BCE所成角的正弦值.图K43-916.(12分)如图K43-10,已知正三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,动点F在侧棱CC1上,且不与点C重合.(1)当CF=1时,求证:EF⊥A1C;(2)设二面角C-AF-E的大小为θ,求tanθ的最小值.图K43-103答案解析【基础热身】1.A[解析]可知A(2,0,0)、B(2,2,0)、C(0,2,0),令P(0,0,2m)(m>0),则E(1,1,m),AE=(-1,1,m),DP=(0,0,2m),∴cos〈DP,AE〉==,m=1.∴E的坐标为(1,1,1).2.D[解析]根据共线向量定理,显然a,b不平行,所以l1,l2的位置关系是相交或异面.3.B[解析]两平面的一个单位法向量n0=,故两平面间的距离d=|OA·n0|=.4.D[解析]直线l的一个单位法向量s0=,向量OA=(1,0,0),故点O到直线l的距离为d===.【能力提升】5.C[解析]建立如图所示的空间直角坐标系.则A(2,0,0),D(0,0,0),D1(0,0,1),C1(0,2,1),AD1=(-2,0,1),DC1=(0,2,1),故异面直线AD1和C1D所成角的余弦值为|cos〈AD1,DC1〉|==.6.D[解析] ∠ACD=90°,∴AC·CD=0.同理BA·AC=0, AB和CD成60°角,∴〈BA,CD〉=60°或120°. BD=BA+AC+CD,∴BD2=BA2+AC2+CD2+2BA·CD+2BA·AC+2AC·CD=BA2+AC2+CD2+2BA·CD=3+2×1×1×cos〈BA,CD〉=∴|BD|=2或,即B、D间的距离为2或,故选D.7.D[解析]建立如图所示的空间直角坐标系,设正方体棱长为1,则有A(0,0,0),D...