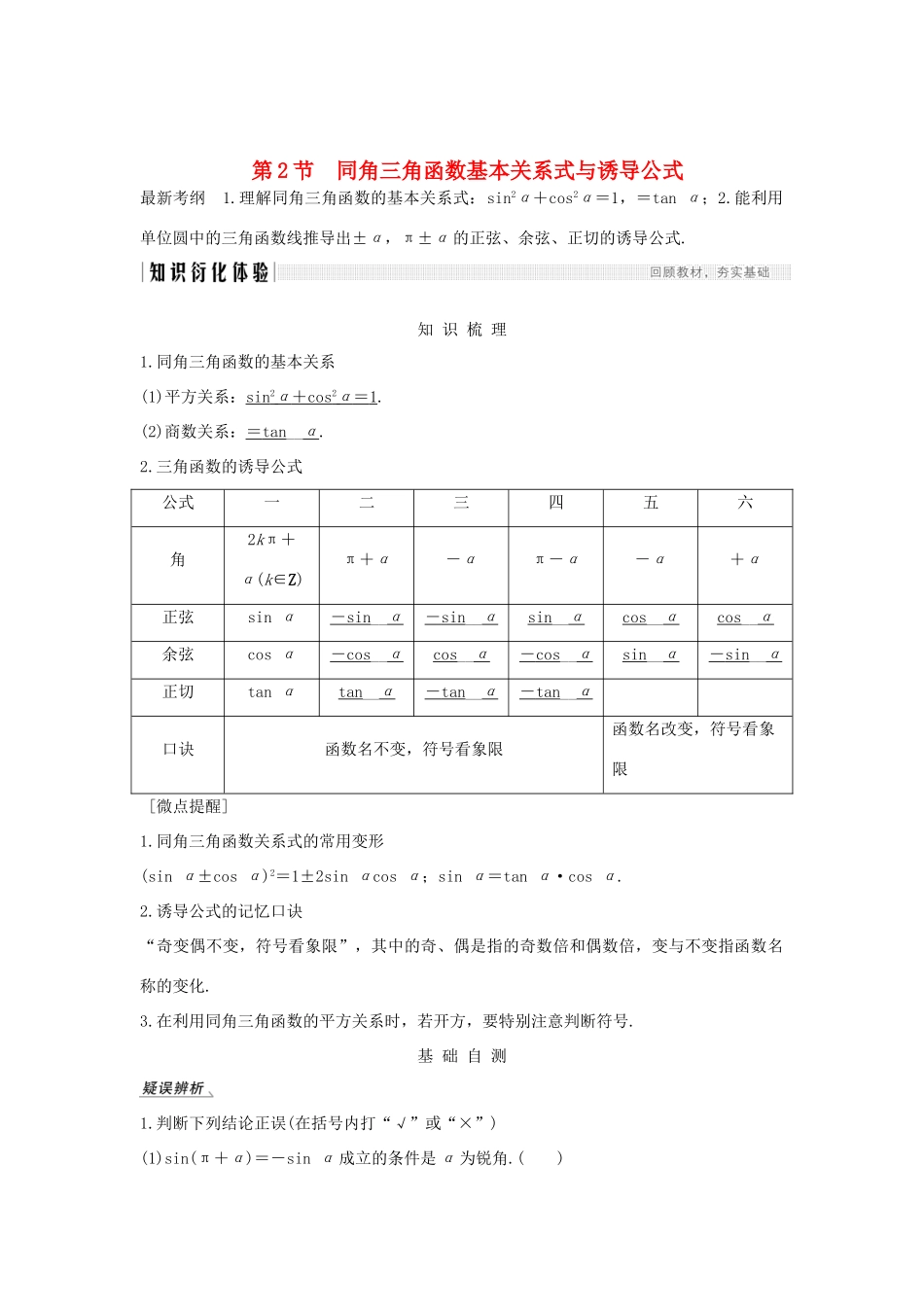
第2节同角三角函数基本关系式与诱导公式最新考纲1.理解同角三角函数的基本关系式:sin2α+cos2α=1,=tanα;2.能利用单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式.知识梳理1.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1.(2)商数关系:=tan__α.2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sinα-sin__α-sin__αsin__αcos__αcos__α余弦cosα-cos__αcos__α-cos__αsin__α-sin__α正切tanαtan__α-tan__α-tan__α口诀函数名不变,符号看象限函数名改变,符号看象限[微点提醒]1.同角三角函数关系式的常用变形(sinα±cosα)2=1±2sinαcosα;sinα=tanα·cosα.2.诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.3.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.基础自测1.判断下列结论正误(在括号内打“√”或“×”)(1)sin(π+α)=-sinα成立的条件是α为锐角.()(2)六组诱导公式中的角α可以是任意角.()(3)若α∈R,则tanα=恒成立.()(4)若sin(kπ-α)=(k∈Z),则sinα=.()解析(1)中对于任意α∈R,恒有sin(π+α)=-sinα.(3)中当α的终边落在y轴上,商数关系不成立.(4)当k为奇数时,sinα=,当k为偶数时,sinα=-.答案(1)×(2)√(3)×(4)×2.(必修4P21A12改编)已知tanα=-3,则cos2α-sin2α=()A.B.-C.D.-解析由同角三角函数关系得cos2α-sin2α====-.答案B3.(必修4P29B2改编)已知α为锐角,且sinα=,则cos(π+α)=()A.-B.C.-D.解析因为α为锐角,所以cosα==,故cos(π+α)=-cosα=-.答案A4.(2017·全国Ⅲ卷)已知sinα-cosα=,则sin2α=()A.-B.-C.D.解析 (sinα-cosα)2=1-2sinαcosα=1-sin2α,∴sin2α=1-=-.答案A5.(2019·济南质检)若sinα=-,且α为第四象限角,则tanα=()A.B.-C.D.-解析 sinα=-,α为第四象限角,∴cosα==,因此tanα==-.答案D6.(2018·成都月考)化简:=________.解析原式===1.答案1考点一同角三角函数基本关系式的应用【例1】(1)(2018·兰州测试)已知sinαcosα=,且<α<,则cosα-sinα=()A.-B.C.-D.(2)(2019·平顶山联考)已知=5,则cos2α+sin2α=()A.B.-C.-3D.3解析(1) <α<,∴cosα<0,sinα<0且cosα>sinα,∴cosα-sinα>0.又(cosα-sinα)2=1-2sinαcosα=1-2×=,∴cosα-sinα=.(2)由=5得=5,可得tanα=2,则cos2α+sin2α=cos2α+sinαcosα===.答案(1)B(2)A规律方法1.利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tanα可以实现角α的弦切互化.2.应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.3.注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.【训练1】(1)若3sinα+cosα=0,则的值为()A.B.C.D.-2(2)(2018·全国Ⅱ卷)已知sinα+cosβ=1,cosα+sinβ=0,则sin(α+β)=________.解析(1)3sinα+cosα=0⇒cosα≠0⇒tanα=-,====.(2)由sinα+cosβ=1,cosα+sinβ=0,两式平方相加,得2+2sinαcosβ+2cosαsinβ=1,整理得sin(α+β)=-.答案(1)A(2)-考点二诱导公式的应用【例2】(1)(2019·衡水中学调研)若cos=,则cos(π-2α)=()A.B.C.-D.-(2)设f(α)=(1+2sinα≠0),则f=________.解析(1)由cos=,得sinα=.∴cos(π-2α)=-cos2α=-(1-2sin2α)=2sin2α-1=2×-1=-.(2) f(α)====,∴f===.答案(1)D(2)规律方法1.诱导公式的两个应用(1)求值:负化正,大化小,化到锐角为终了.(2)化简:统一角,统一名,同角名少为终了.2.含2π整数倍的诱导公式的应用由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cosα.【训练2】(1)(2017·北京卷)在平面直角坐标...