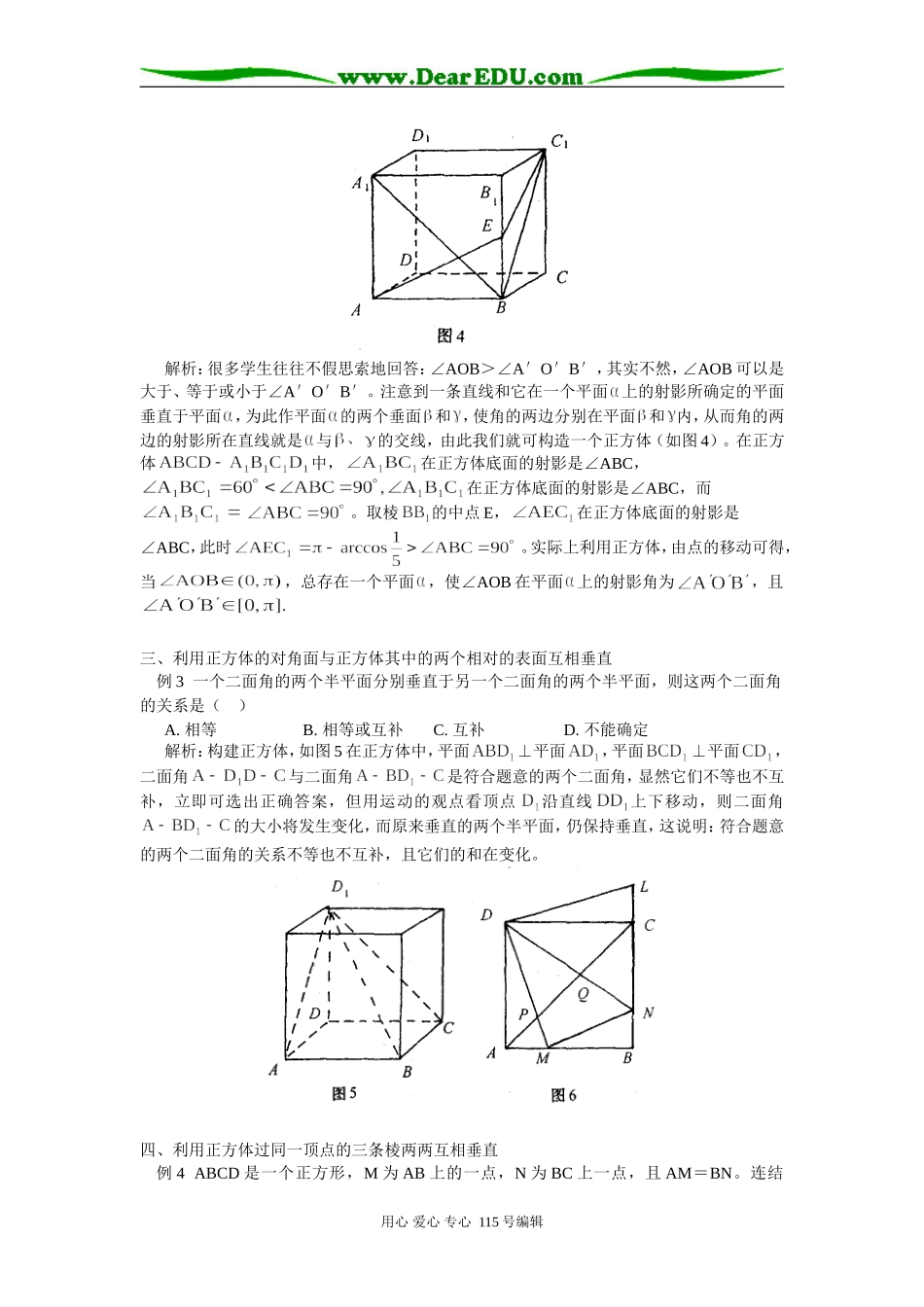
正方体在解题中的模型作用李建标有些立体几何题由于线面关系复杂。空间想象能力要求高,学生往往感到畏惧。而正方体由于图形对称完美,具有其他图形难以企及的性质,如果能挖掘题设条件,展开联想,构造出相应的正方体,其特性即可得到充分利用,使解题过程简捷明快,生动有趣。本文谈谈利用正方体的性质构造正方体的思维策略。一、利用几何体可内接于正方体例1已知平面及以下三个几何体:(1)长、宽、高皆不相等的长方体;(2)底面为平行四边形但不是矩形和菱形的四棱锥;(3)正四面体。这三个几何体在平面上的射影可以是正方形的几何体是__________。解析:此题如果把这三个几何体直接投影到平面上,再判断所得射影是否是正方形是很困难的。但如图1~图3所示构造正方体的内接长方体(图1),四棱锥(图2),正四面体(图3),易知它们在正方体的底面射影都是正方形。故答案是①、②、③。二、利用正方体相邻两个面互相垂直例2已知∠AOB在平面内的射影是∠A′O′B′,其中A′、O′、B′分别是点A、O、B平面内射影,且A′、O′、B′不共线。比较∠AOB与∠A′O′B′的大小。用心爱心专心115号编辑解析:很多学生往往不假思索地回答:∠AOB>∠A′O′B′,其实不然,∠AOB可以是大于、等于或小于∠A′O′B′。注意到一条直线和它在一个平面上的射影所确定的平面垂直于平面,为此作平面的两个垂面和,使角的两边分别在平面和内,从而角的两边的射影所在直线就是与的交线,由此我们就可构造一个正方体(如图4)。在正方体中,在正方体底面的射影是∠ABC,在正方体底面的射影是∠ABC,而。取棱的中点E,在正方体底面的射影是∠ABC,此时。实际上利用正方体,由点的移动可得,当,总存在一个平面,使∠AOB在平面上的射影角为,且三、利用正方体的对角面与正方体其中的两个相对的表面互相垂直例3一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角的关系是()A.相等B.相等或互补C.互补D.不能确定解析:构建正方体,如图5在正方体中,平面⊥平面,平面⊥平面,二面角与二面角是符合题意的两个二面角,显然它们不等也不互补,立即可选出正确答案,但用运动的观点看顶点沿直线上下移动,则二面角的大小将发生变化,而原来垂直的两个半平面,仍保持垂直,这说明:符合题意的两个二面角的关系不等也不互补,且它们的和在变化。四、利用正方体过同一顶点的三条棱两两互相垂直例4ABCD是一个正方形,M为AB上的一点,N为BC上一点,且AM=BN。连结用心爱心专心115号编辑DM、DN分别交对角线AC于点P、Q,剪掉△MNB,求证:(1)以DM、DN为折痕,将DA与DC重合,可以构成一个三棱锥的侧面;(2)以线段AP、PQ、QC为边恰好可以构成一个内角为60°的三角形。证明:(1)如图6,延长NC到L,使CL=BN。易知△DCL≌△DAM,所以DL=DM,∠LDC=∠MDA,在△DMN与△DLN中,MN<MB+BN=AB=LN,DL=DM,DN=DN,所以∠MDN<∠LDN=∠LDC+∠CDN=∠MDA+∠CDN。从而可以DM、DN为折痕,使DA与DC重合构成一个三棱锥的侧面。(2)形成上述三棱锥后,A、C重合,AP、PQ、QC恰分别在三个侧面内,如图7构成一个三角形APQ。由于∠DAM=∠DAN=90°,而所以∠MAN=90°。在A点汇集了三条两两互相垂直的射线,有如正方体的一个角,而AP平分∠DAM(∠PAM=45°),QA平分∠DAN(∠QAN=45°),所以∠PAQ可以看作是正方体从一个顶点A出发的两个侧面对角线间的夹角。如图容易求解∠PAQ=60°。五、利用正方体的棱与棱的位置关系例5存在几条两两异面的直线,使得没有任何直线能与之同时相交?解析:对于三条两两异面的直线存在无数条直线与之相交。如图8在正方体中,两两异面。在上取一点F,连结,过A点作的平行线交BC于E,连结EF。直线EF与所在直线必相交。由F的任意性可知,和都相交的直线有无数条,且无数条直线也异面。对于4条两两异面的直线则不存在直线与之都相交。取正方体,则直线两两成异面直线,假设存在一条直线l与直线AB交于E,与直线交于F,与直线交于G,与直线交于H。现将整个图形绕旋转120°(如图9),由于⊥面且通过正的中心故点A变为点,点变为点,点变为点A;同样点B变为点,点...