怎样理解充分条件、必要条件和充要条件 专题辅导 不分版本VIP免费

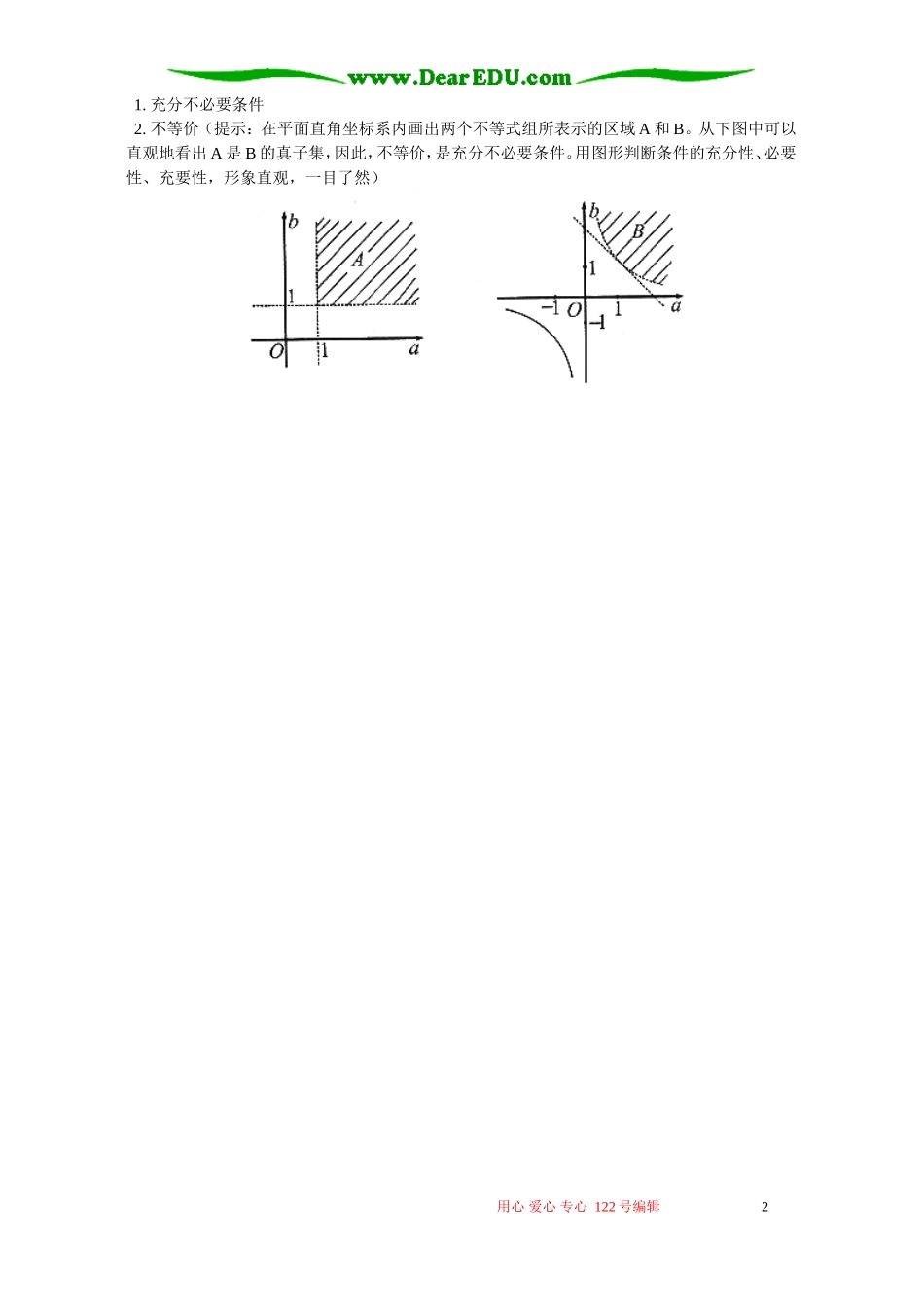
怎样理解充分条件、必要条件和充要条件张万库充分条件、必要条件和充要条件是简易逻辑中的重要概念，准确理解、有意识地运用这几个概念思考问题和解决问题，可以使同学们养成严谨的思维品质，提高大家的逻辑思维能力。怎样理解这三个概念呢？1.充分条件、必要条件和充要条件反映的是一个命题中条件和结论间的因果关系（条件关系），是条件对于结论成立的作用。谈一个命题的条件是否充分、必要、充要时，这个命题必须是确定的。2.充分条件的特征是“有之必然，无之未必不然”，即对于给定的命题“若A则B”，有了条件A，结论B一定成立（AB）；没有条件A，结论B未必不成立，也有可能成立。这样的条件A就是结论B的充分条件。例如，在命题“若x>0，则x20”中，有了条件“x>0”，就一定有结论“x20”成立。把条件“x>0”换成“x0”或“x0”，仍有结论“x20”成立。因此条件“x0”是结论“x20”的充分条件。教材中由“pq”定义“p是q的充分条件”，说的就是命题“若p则q”中条件p对于结论q成立的作用。3.必要条件的特征是“无之必不然，有之未必然”，即对于给定的命题“若A则B”，没有条件A，结论B一定不成立（AB）；但是有了条件A，结论B却未必一定成立。这样的条件A就是结论B的必要条件。例如，在命题“若xRxQ，则”中，没有条件“xQ”，就一定不会有结论“xQ”。但是有了条件“xR”，却未必有结论“xR”，还有可能是xCQR。因此条件“xR”是结论“xQ”的必要条件。利用“AB”判断条件A是结论B的必要条件，有时是很困难的。我们可以利用“AB”的等价命题“BA”来判断，但一定要注意A还是条件，B还是结论，即若由结论B能推出条件A，则条件A对于结论B的成立是必要的。教材中由“pq”定义“q是p的必要条件”，说的就是命题“若q则p”中条件q对于结论p成立的作用（qp）。4.充要条件的特征是“有之必然，无之必不然”，即对于给定的命题“若A则B”，有了条件A，结论B一定成立（AB）；没有条件A，结论B一定不成立（AB即BA）。这样的条件A就是结论B的充要条件。例如，在命题“△ABC中，若∠∠∠ABC，则BC=CA=AB”中，有了条件“∠A=∠B=∠C”，就一定有结论“BC=CA=AB”成立；反之没有条件“∠A=∠B=∠C”，就一定没有结论“BC=CA=AB”成立（即有了“BC=CA=AB”，也一定有“∠A=∠B=∠C”）。因此条件“∠A=∠B=∠C”是结论“BC=CA=AB”的充要条件。弄懂了充分条件、必要条件的本质，教材中由“pq”定义“p是q的充要条件”则是不难理解的。5.在命题“若A则B”中，条件A是结论B的充分（必要、充要）条件，在逆命题“若B则A”中，条件B就是结论A的必要（充分、充要）条件。运用充分条件、必要条件、充要条件的概念和观点思考问题、解决问题时，一定要弄清问题中所涉及的命题是什么（即弄清谁是条件，谁是结论）。点评：充分条件、必要条件和充要条件的学习与运用，是一个极好的思维训练资源。只要准确理解、有意识运用这几个概念思考问题和解决问题，同学们就可以少犯错误，变得聪明起来。练一练：1.已知a，b，c是常数，则“a>0且bac240”是“对任意xRaxbxc，20恒成立”的什么条件？2.我们知道ababab1121，与是等价的，那么ab11与abab21是否也等价呢？答案：用心爱心专心122号编辑11.充分不必要条件2.不等价（提示：在平面直角坐标系内画出两个不等式组所表示的区域A和B。从下图中可以直观地看出A是B的真子集，因此，不等价，是充分不必要条件。用图形判断条件的充分性、必要性、充要性，形象直观，一目了然）用心爱心专心122号编辑2