通州市兴仁中学高二数学期末模拟试卷(三)VIP免费

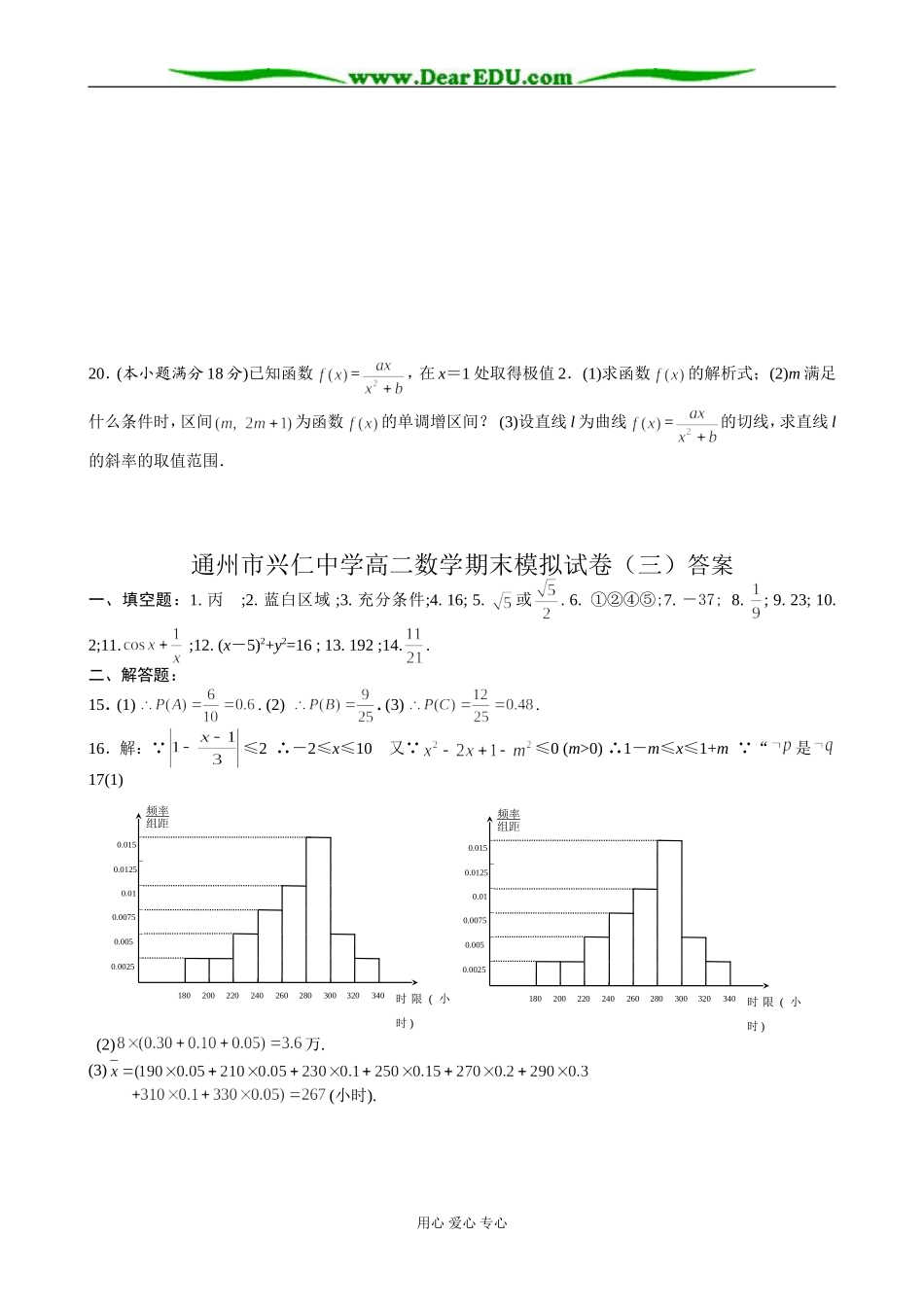
红蓝黄白S1WhileS<10SS+3M2S+3EndwhilePrintM通州市兴仁中学高二数学期末模拟试卷（三）一、填空题：本大题共14小题，每小题5分，共70分．1．甲、乙、丙、丁四名射击选手所得的平均环数及其方差S2如下表所示，则选送参加决赛的最佳人选是.2．如图，将一个长与宽不等的长方形水平放置，长方形对角线将其分成四个区域，在四个区域内涂上红、蓝、黄、白四种颜色，并在中间装个指针，使其可以自由转动，指针停留的可能性大的区域是.3．已知真命题“”和“”，那么“”是“”的条件.4．以原点为顶点，椭圆C：的左准线为准线的抛物线交椭圆C的右准线于A，B两点，则等于.5．已知对称轴为坐标轴的双曲线有一条渐近线平行于直线x＋2y－3＝0，则该双曲线的离心率为.6.坐标平面上有相异两个定点A，B和动点P，如果直线PA、PB的斜率之积为定值m，则点P的轨迹可能在以下那些曲线上：①椭圆；②双曲线；③抛物线；④圆；⑤直线．答：(写出你认为正确的所有曲线的序号)..7．已知(a为常数)在[－2，2]上有最大值3，那么在[－2，2]上f(x)的最小值是.8．同时投掷大小不同的两颗骰子，所得点数之和是5的概率是.9.根据如图所示的伪代码，可知输出的结果M为.10．已知F1和F2是两个定点，点P是以F1和F2为公共焦点的椭圆和双曲线的一个交点，并且,分别是椭圆和双曲线的离心率，则有.11．已知函数，则=．12．以椭圆=1的右焦点为圆心，且与双曲线=1的渐近线相切的圆的方程为．13．某校有教师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本，已知从女学生中抽取的人数为80人，则n的值为．14．某徒工加工外形完全一样的甲、乙两种零件.他加工的5个甲种零件中有2个次品，2个乙种零件中有1个次品，现从这7个零件中随机抽取2个，则能查到甲种零件的次品的概率为（结果用分数表示）.二、解答题：本大题共6小题，共90分．15．(本小题满分15分)一个口袋内装有大小相同的2个白球和3个黑球．(1)从中一次摸出两个球，求两球恰好颜色不同的概率；(2)从中摸出一个球，放回后再摸出一个球，求两球同时是黑球的概率；(3)从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率．16．(本小题满分12分)已知p：≤2；q：≤0(m>0)，若是的充分而不必要条用心爱心专心甲乙丙丁8998S25.76.25.76.4PABMl··FECDABHOxy8m18mAFCDEB件，求实数m的取值范围．17．(本小题满分15分)为检查某工厂所产8万台电扇的质量,抽查了其中20台的无故障连续使用时限如下：248256232243188268278266289312274296288302295228287217329283(1)完成下面的频率分布表,并在给出的坐标系中作出频率分布直方图．(2)估计8万台电扇中有多少台无故障连续使用时限会超过280小时．(3)用组中值估计样本的平均无故障连续使用时限．18.(本小题满分15分)如下左图是抛物线型拱桥，设水面宽AB=18m，拱顶离水面的距离是8m，一货船在水面上的横断面为矩形CDEF．(1)以拱顶为坐标原点，建立如下右图所示的直角坐标系，若矩形的长CD=9m，那么矩形的高DE不能超过多少米才能使船通过拱桥？(2)求矩形CDEF面积S的“临界值”M(即当SM时，适当调整矩形的长和宽，船能通过拱桥；而当S>M时，无论怎样调整矩形的长和宽，船都不能通过拱桥)．19．(本小题满分15分)已知定点A、B间的距离为2，以B为圆心作半径为2的圆，P为圆上一点，线段AP的垂直平分线l与直线PB交于点M，当P在圆周上运动时点M的轨迹记为曲线C．(1)建立适当的坐标系，求曲线C的方程，并说明它是什么样的曲线；(2)试判断l与曲线C的位置关系，并加以证明．用心爱心专心分组频数频率频率组距合计0.05频率组距时限(小时)0.00250.0050.00750.010.01250.015180200220240260280300320340频率组距时限(小时)0.00250.0050.00750.010.01250.01518020022024026028030032034020．(本小题满分18分)已知函数=，在x＝1处取得极值2．(1)求函数的解析式；(2)m满足什么条件时，区间为函数的单调增区间？(3)设直线l为曲线=的切线，求直线l的斜率的取值范围．通州市兴仁中学高二数学期末模拟试卷（三）答案一、填空题：1.丙;2.蓝白区域;3.充分条件;4.16;5.或.6.①②④⑤;7.－37;8.;9.23;10.2;11.;12...