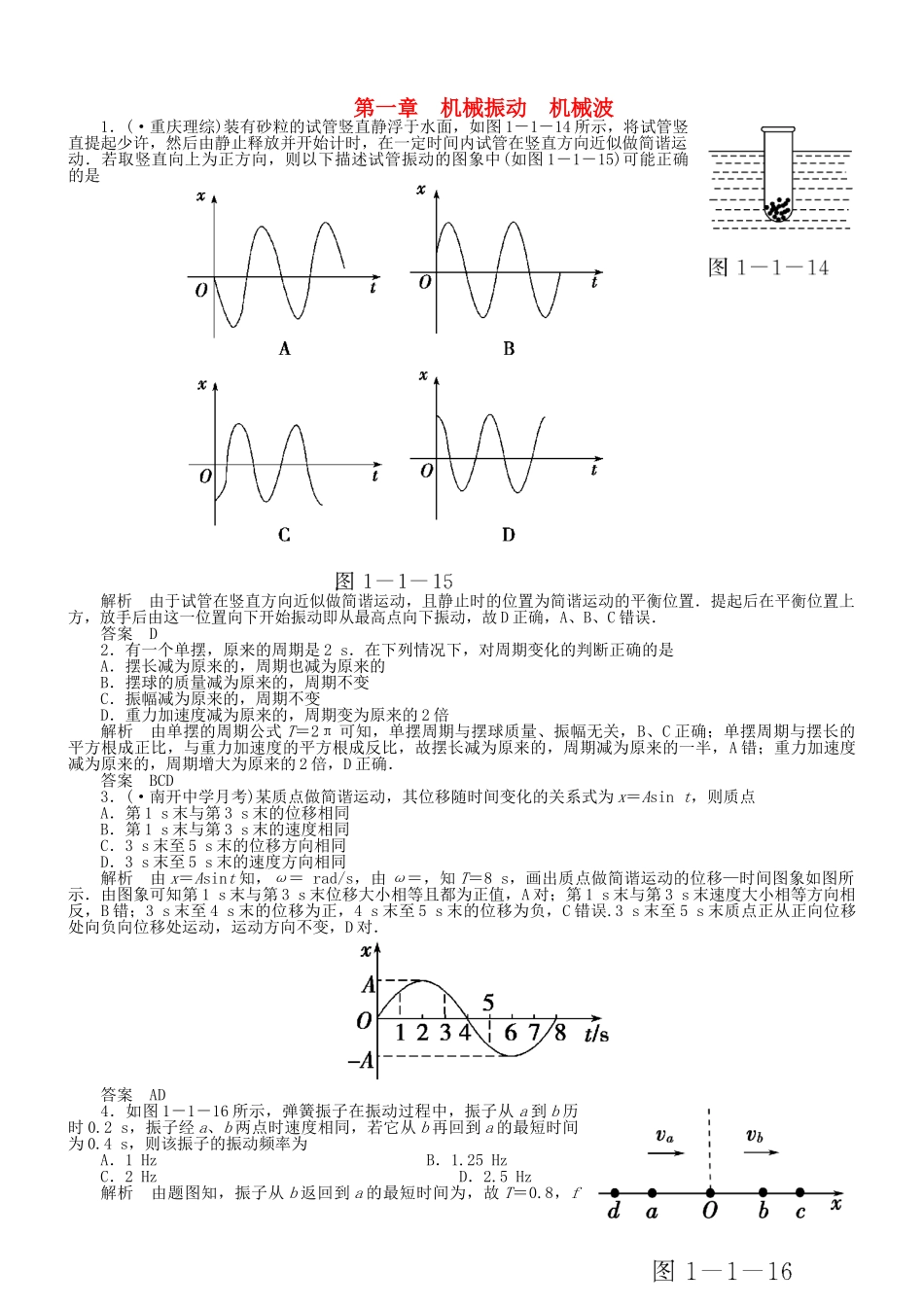
第一章机械振动机械波1.(·重庆理综)装有砂粒的试管竖直静浮于水面,如图1-1-14所示,将试管竖直提起少许,然后由静止释放并开始计时,在一定时间内试管在竖直方向近似做简谐运动.若取竖直向上为正方向,则以下描述试管振动的图象中(如图1-1-15)可能正确的是解析由于试管在竖直方向近似做简谐运动,且静止时的位置为简谐运动的平衡位置.提起后在平衡位置上方,放手后由这一位置向下开始振动即从最高点向下振动,故D正确,A、B、C错误.答案D2.有一个单摆,原来的周期是2s.在下列情况下,对周期变化的判断正确的是A.摆长减为原来的,周期也减为原来的B.摆球的质量减为原来的,周期不变C.振幅减为原来的,周期不变D.重力加速度减为原来的,周期变为原来的2倍解析由单摆的周期公式T=2π可知,单摆周期与摆球质量、振幅无关,B、C正确;单摆周期与摆长的平方根成正比,与重力加速度的平方根成反比,故摆长减为原来的,周期减为原来的一半,A错;重力加速度减为原来的,周期增大为原来的2倍,D正确.答案BCD3.(·南开中学月考)某质点做简谐运动,其位移随时间变化的关系式为x=Asint,则质点A.第1s末与第3s末的位移相同B.第1s末与第3s末的速度相同C.3s末至5s末的位移方向相同D.3s末至5s末的速度方向相同解析由x=Asint知,ω=rad/s,由ω=,知T=8s,画出质点做简谐运动的位移—时间图象如图所示.由图象可知第1s末与第3s末位移大小相等且都为正值,A对;第1s末与第3s末速度大小相等方向相反,B错;3s末至4s末的位移为正,4s末至5s末的位移为负,C错误.3s末至5s末质点正从正向位移处向负向位移处运动,运动方向不变,D对.答案AD4.如图1-1-16所示,弹簧振子在振动过程中,振子从a到b历时0.2s,振子经a、b两点时速度相同,若它从b再回到a的最短时间为0.4s,则该振子的振动频率为A.1HzB.1.25HzC.2HzD.2.5Hz解析由题图知,振子从b返回到a的最短时间为,故T=0.8,f==1.25Hz,B正确.答案B5.在接近收费口的道路上安装了若干条突起于路面且与行驶方向垂直的减速带,减速带间距为10m,当车辆经过减速带时会产生振动.若某汽车的固有频率为1.25Hz,则当该车以________m/s的速度行驶在此减速区时颠簸得最厉害,我们把这种现象称为________.解析由车辆颠簸得最厉害可知车发生共振现象.由共振条件f驱=f固得f车=1.25Hz,由公式v==s·f得v=12.5m/s.答案12.5共振6.(·厦门期末)某同学用单摆测重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当做摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L-T2图线,然后在图线上选取A、B两点,坐标如图1-1-17所示.他计算重力加速度的表达式应为g=________.请你判断该同学得到的结果与摆球重心就在球心处的情况相比,将________(填“偏大”“偏小”或“相同”).答案相同7.弹簧振子以O点为平衡位置,在B、C两点间做简谐运动,在t=0时刻,振子从O、B间的P点以速度v向B点运动;在t=0.2s时,振子速度第一次变为-v;在t=0.5s时,振子速度第二次变为-v.(1)求弹簧振子振动周期T.(2)若B、C之间的距离为25cm,求振子在4.0s内通过的路程.(3)若B、C之间的距离为25cm.从平衡位置计时,写出弹簧振子位移表达式,并画出弹簧振子的振动图象.解析(1)弹簧振子简谐运动示意图如图由对称性可得:T=0.5×2s=1.0s(2)若B、C之间距离为25cm,则振幅A=×25cm=12.5cm振子4.0s内通过的路程s=4×4×12.5cm=200cm(3)根据x=Asinωt,A=12.5cm,ω==2πrad/s.得x=12.5sin2πt(cm).振动图象为答案(1)1.0s(2)200cm(3)x=12.5sin2πt(cm)图象见解析