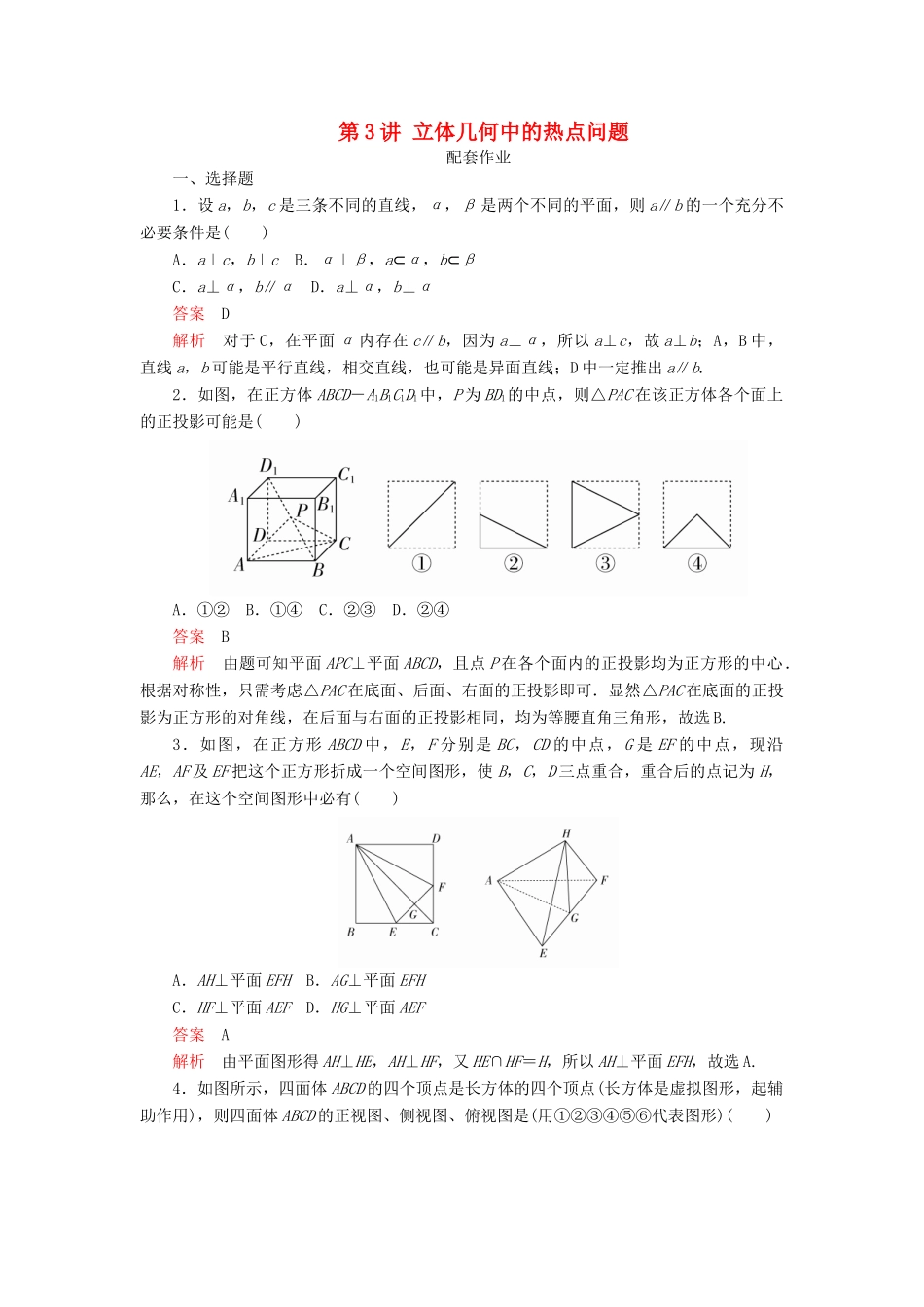
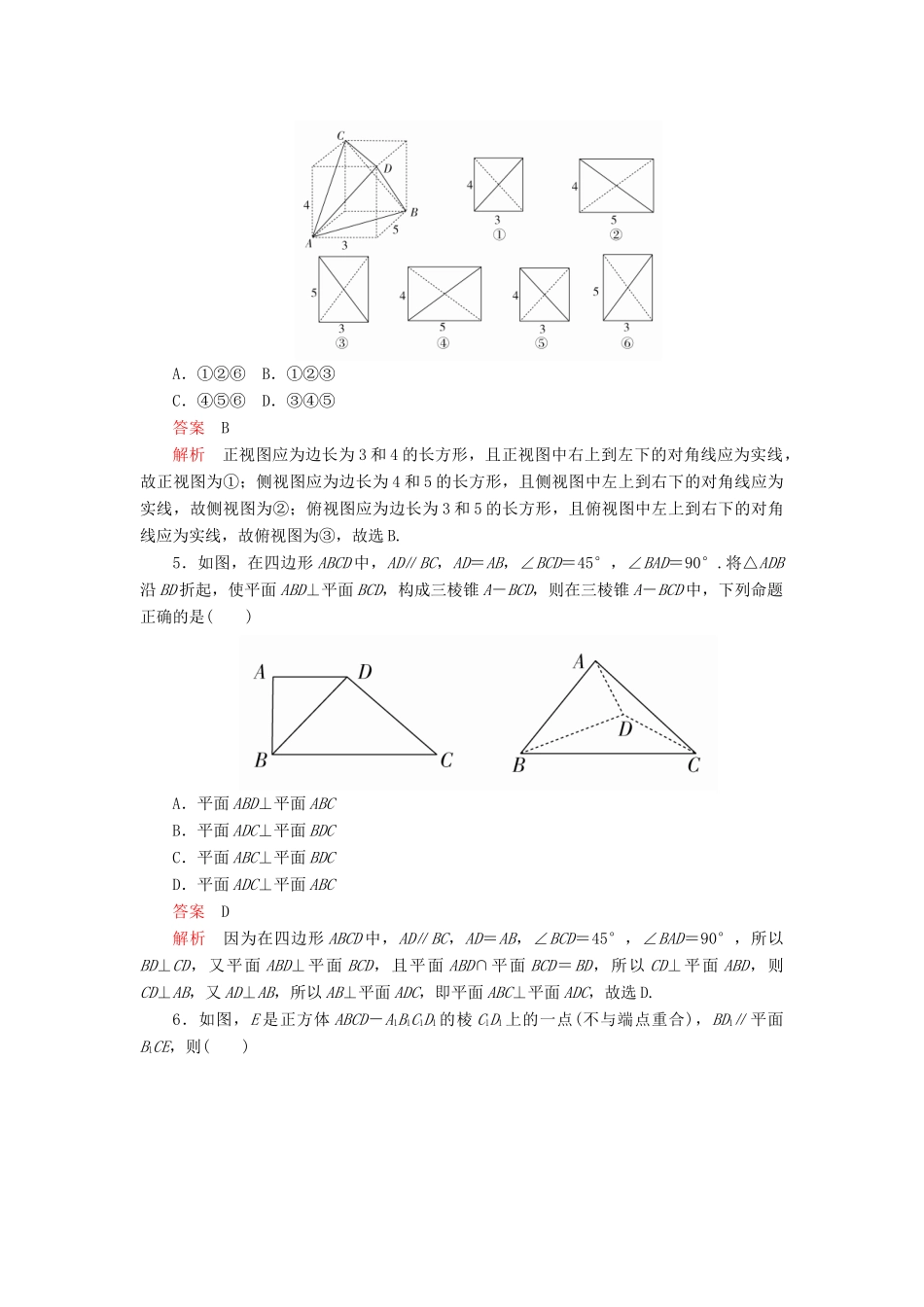
第3讲立体几何中的热点问题配套作业一、选择题1.设a,b,c是三条不同的直线,α,β是两个不同的平面,则a∥b的一个充分不必要条件是()A.a⊥c,b⊥cB.α⊥β,a⊂α,b⊂βC.a⊥α,b∥αD.a⊥α,b⊥α答案D解析对于C,在平面α内存在c∥b,因为a⊥α,所以a⊥c,故a⊥b;A,B中,直线a,b可能是平行直线,相交直线,也可能是异面直线;D中一定推出a∥b.2.如图,在正方体ABCD-A1B1C1D1中,P为BD1的中点,则△PAC在该正方体各个面上的正投影可能是()A.①②B.①④C.②③D.②④答案B解析由题可知平面APC⊥平面ABCD,且点P在各个面内的正投影均为正方形的中心.根据对称性,只需考虑△PAC在底面、后面、右面的正投影即可.显然△PAC在底面的正投影为正方形的对角线,在后面与右面的正投影相同,均为等腰直角三角形,故选B.3.如图,在正方形ABCD中,E,F分别是BC,CD的中点,G是EF的中点,现沿AE,AF及EF把这个正方形折成一个空间图形,使B,C,D三点重合,重合后的点记为H,那么,在这个空间图形中必有()A.AH⊥平面EFHB.AG⊥平面EFHC.HF⊥平面AEFD.HG⊥平面AEF答案A解析由平面图形得AH⊥HE,AH⊥HF,又HE∩HF=H,所以AH⊥平面EFH,故选A.4.如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的正视图、侧视图、俯视图是(用①②③④⑤⑥代表图形)()A.①②⑥B.①②③C.④⑤⑥D.③④⑤答案B解析正视图应为边长为3和4的长方形,且正视图中右上到左下的对角线应为实线,故正视图为①;侧视图应为边长为4和5的长方形,且侧视图中左上到右下的对角线应为实线,故侧视图为②;俯视图应为边长为3和5的长方形,且俯视图中左上到右下的对角线应为实线,故俯视图为③,故选B.5.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列命题正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC答案D解析因为在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,所以BD⊥CD,又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,所以CD⊥平面ABD,则CD⊥AB,又AD⊥AB,所以AB⊥平面ADC,即平面ABC⊥平面ADC,故选D.6.如图,E是正方体ABCD-A1B1C1D1的棱C1D1上的一点(不与端点重合),BD1∥平面B1CE,则()A.BD1∥CEB.AC1⊥BD1C.D1E=2EC1D.D1E=EC1答案D解析设B1C∩BC1=O,如图,BD1∥平面B1CE,平面BC1D1∩平面B1CE=OE,所以BD1∥OE.因为O为BC1的中点,所以E为C1D1的中点,所以D正确;由异面直线的定义知BD1,CE是异面直线,故A错;在矩形ABC1D1中,AC1与BD1不垂直,故B错,C显然是错的,所以选D.7.(2018·甘肃二诊)已知长方体ABCD-A1B1C1D1中,AA1=,AB=4,若在棱AB上存在点P,使得D1P⊥PC,则AD的取值范围是()A.(0,1]B.(0,2]C.(1,]D.[1,4)答案B解析连接DP,由D1P⊥PC,DD1⊥PC,且D1P,DD1是平面DD1P上两条相交直线,得PC⊥平面DD1P,PC⊥DP,即点P在以CD为直径的圆上,又点P在AB上,则AB与圆有公共点,即0<AD≤CD=2,故选B.二、填空题8.(2017·泉州模拟)点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,给出下列命题:①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1;④平面PDB1⊥平面ACD1.其中正确的命题序号是________.答案①②④解析对于①,VA-D1PC=VP-AD1C点P到面AD1C的距离,即为线BC1与面AD1C的距离,为定值,故①正确;对于②,因为面A1C1B∥面AD1C,所以线A1P∥面AD1C,故②正确;对于③,DB与BC1就成60°角,故③错误;对于④,由于B1D⊥面ACD1,所以面B1DP⊥面ACD1,故④正确.9.已知正方体ABCD-A1B1C1D1,点P是线段AC1上的一动点,当∠BPD最大时,AP∶AC1=________.答案1∶4解析连接AC,BD,交于点O,连接OP,显然OP⊥BD,∠BPD=2∠BPO,要使∠BPD最大,只需∠BPO最大,只需OP最小,此时OP⊥AC1.由平面几何的知识易得,当OP⊥AC1时,AP∶AC1=1∶4.10.(2018·山西太原一模)已知在直角梯形ABCD中,AB⊥AD,CD⊥AD,AB=2AD=2CD=2,将直...