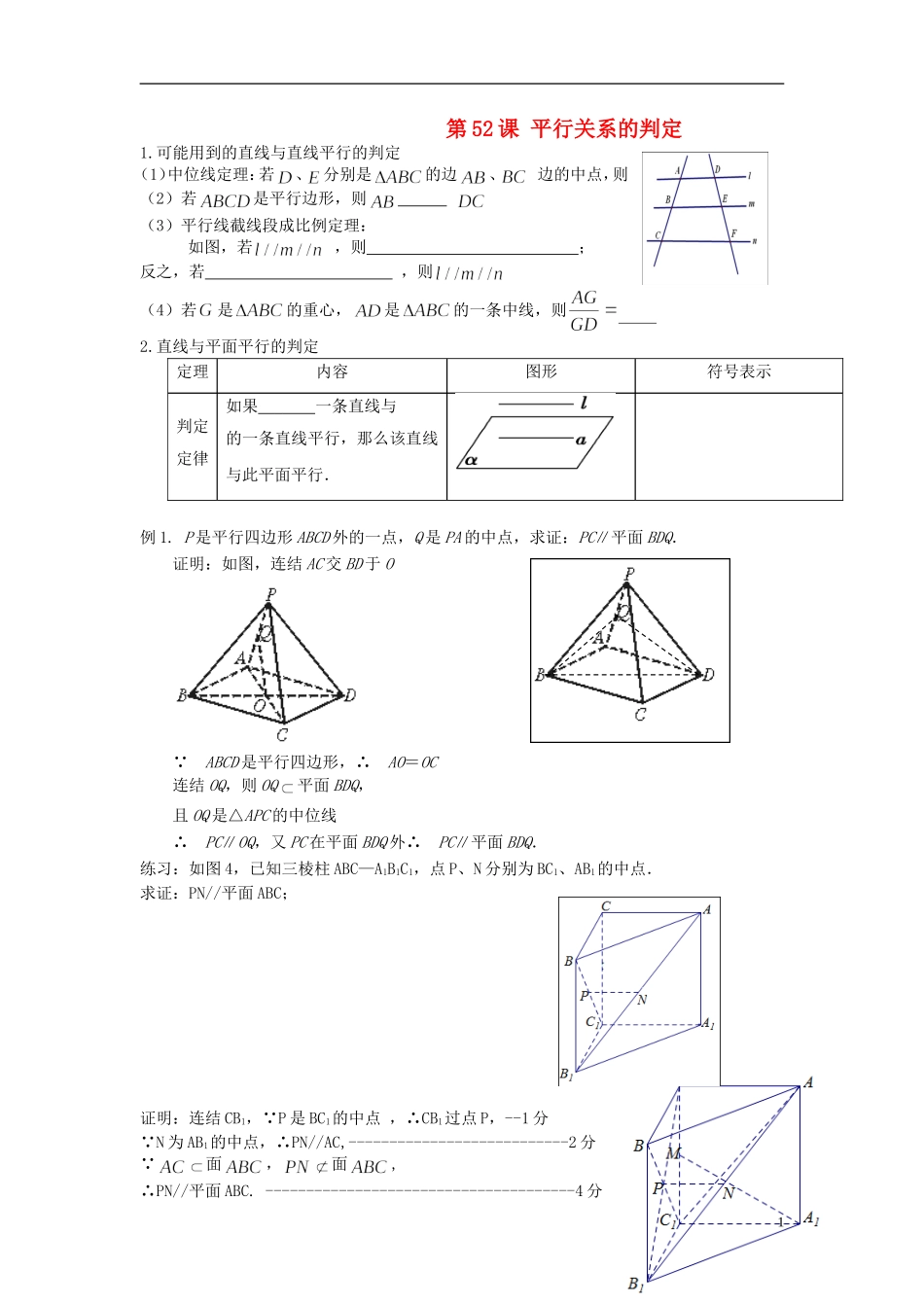
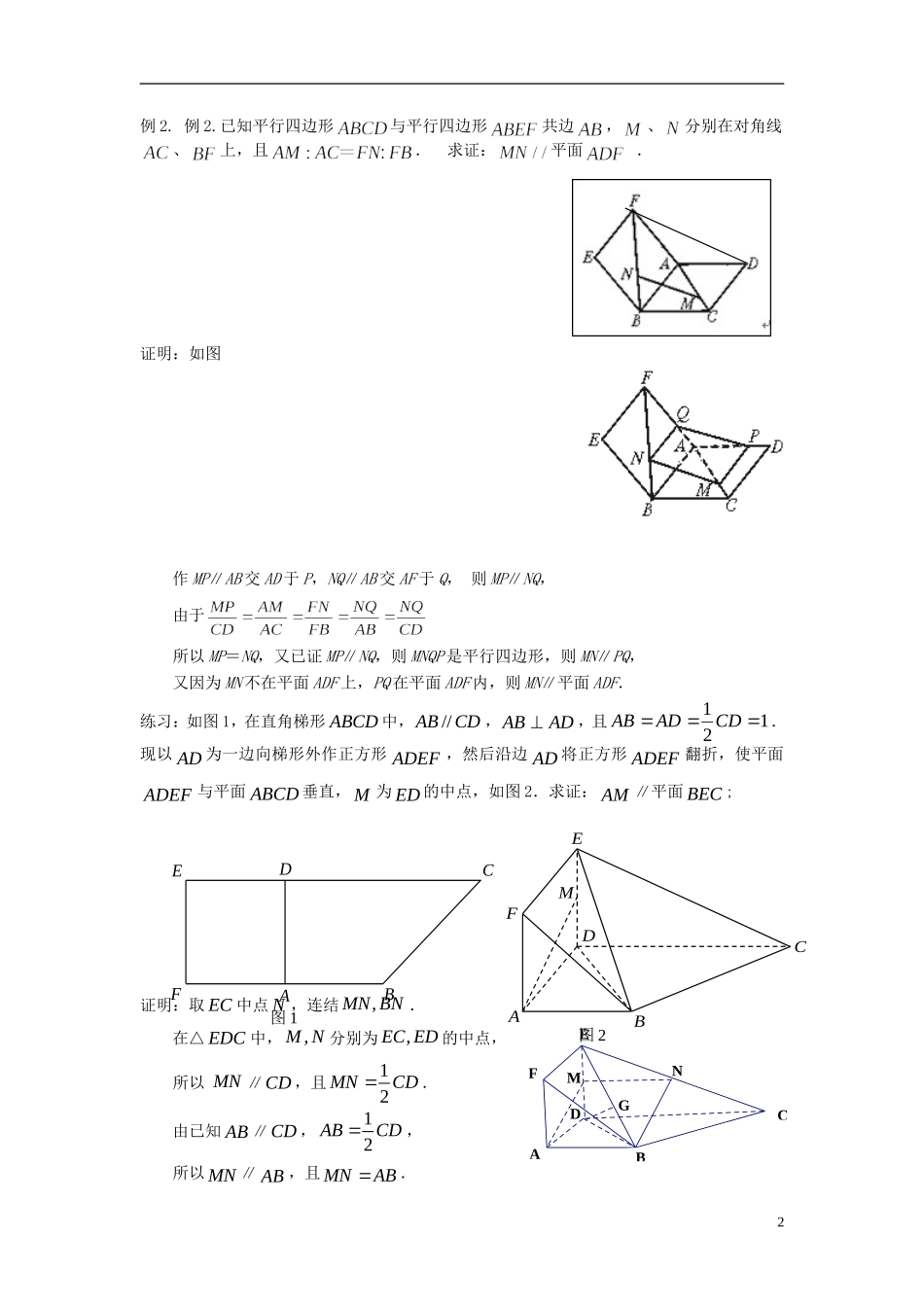
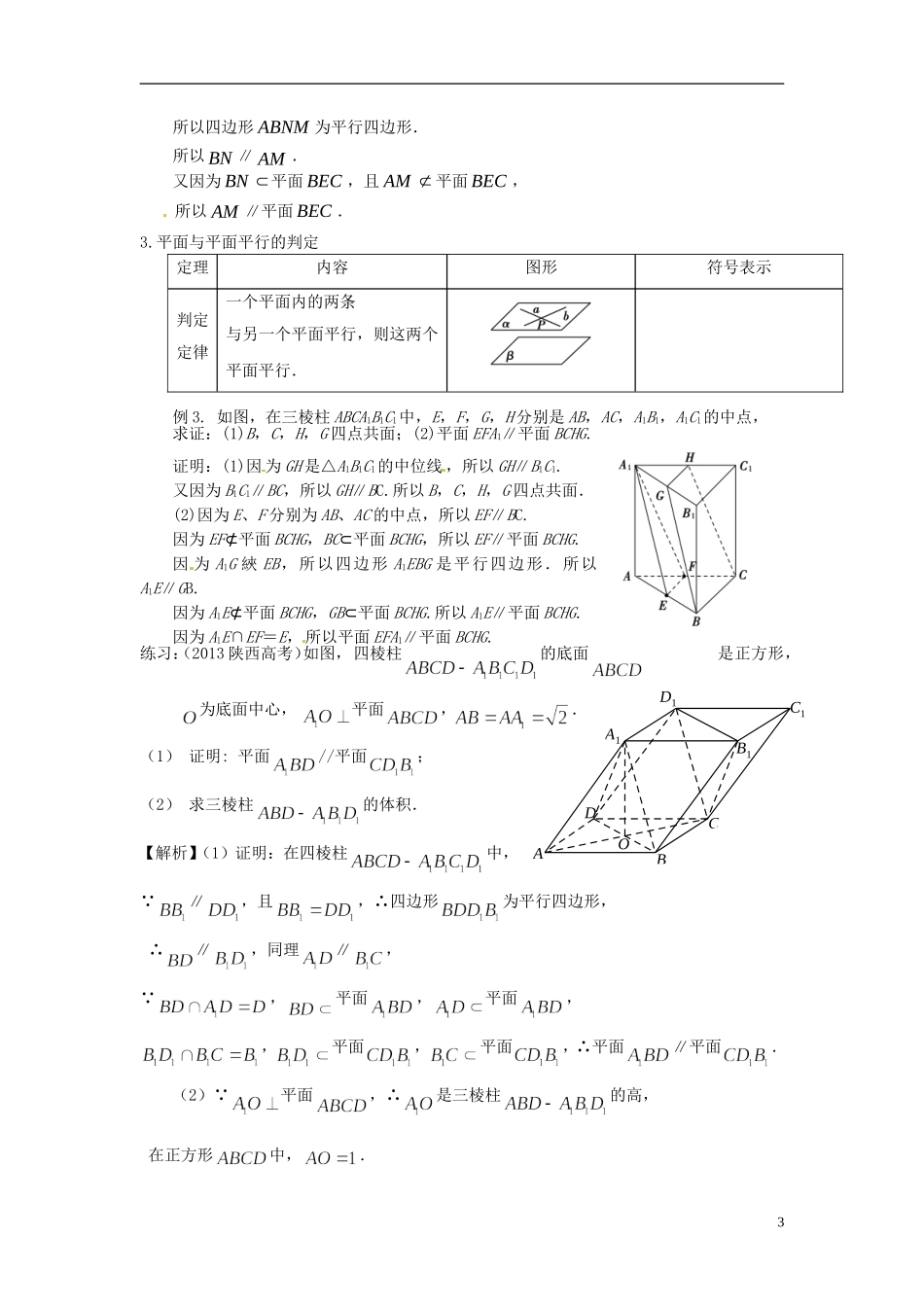
第52课平行关系的判定1.可能用到的直线与直线平行的判定(1)中位线定理:若、分别是的边、边的中点,则(2)若是平行边形,则(3)平行线截线段成比例定理:如图,若,则;反之,若,则(4)若是的重心,是的一条中线,则2.直线与平面平行的判定定理内容图形符号表示判定定律如果一条直线与的一条直线平行,那么该直线与此平面平行.例1.P是平行四边形ABCD外的一点,Q是PA的中点,求证:PC∥平面BDQ.证明:如图,连结AC交BD于O ABCD是平行四边形,∴AO=OC连结OQ,则OQ平面BDQ,且OQ是△APC的中位线∴PC∥OQ,又PC在平面BDQ外∴PC∥平面BDQ.练习:如图4,已知三棱柱ABC—A1B1C1,点P、N分别为BC1、AB1的中点.求证:PN//平面ABC;证明:连结CB1, P是BC1的中点,∴CB1过点P,--1分 N为AB1的中点,∴PN//AC,---------------------------2分 面,面,∴PN//平面ABC.--------------------------------------4分1GMAFBCDEN例2.例2.已知平行四边形与平行四边形共边,、分别在对角线、上,且.求证:平面.证明:如图作MP∥AB交AD于P,NQ∥AB交AF于Q,则MP∥NQ,由于所以MP=NQ,又已证MP∥NQ,则MNQP是平行四边形,则MN∥PQ,又因为MN不在平面ADF上,PQ在平面ADF内,则MN∥平面ADF.练习:如图1,在直角梯形ABCD中,CDAB//,ADAB,且121CDADAB.现以AD为一边向梯形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD垂直,M为ED的中点,如图2.求证:AM∥平面BEC;证明:取EC中点N,连结BNMN,.在△EDC中,,MN分别为,ECED的中点,所以MN∥CD,且12MNCD.由已知AB∥CD,12ABCD,所以MN∥AB,且MNAB.2FEDCBA图1ABCDFE图2MOABCDD1C1B1A1所以四边形ABNM为平行四边形.所以BN∥AM.又因为BN平面BEC,且AM平面BEC,所以AM∥平面BEC.3.平面与平面平行的判定定理内容图形符号表示判定定律一个平面内的两条与另一个平面平行,则这两个平面平行.例3.如图,在三棱柱ABCA1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:(1)B,C,H,G四点共面;(2)平面EFA1∥平面BCHG.证明:(1)因为GH是△A1B1C1的中位线,所以GH∥B1C1.又因为B1C1∥BC,所以GH∥BC.所以B,C,H,G四点共面.(2)因为E、F分别为AB、AC的中点,所以EF∥BC.因为EF⊄平面BCHG,BC⊂平面BCHG,所以EF∥平面BCHG.因为A1G綊EB,所以四边形A1EBG是平行四边形.所以A1E∥GB.因为A1E⊄平面BCHG,GB⊂平面BCHG.所以A1E∥平面BCHG.因为A1E∩EF=E,所以平面EFA1∥平面BCHG.练习:(2013陕西高考)如图,四棱柱的底面是正方形,为底面中心,平面,.(1)证明:平面//平面;(2)求三棱柱的体积.【解析】(1)证明:在四棱柱中, ∥,且,∴四边形为平行四边形,∴∥,同理∥, ,平面,平面,,平面,平面,∴平面∥平面.(2) 平面,∴是三棱柱的高,在正方形中,.3∴,∴.第52课平行关系的判定业题1.对两条不相交的空间直线和,则()A.必定存在平面,使得B.必定存在平面,使得,∥C.必定存在直线,使得∥,∥D.必定存在直线,使得∥,【答案】B2.设,是不同的直线,,是不同的平面,且.则“∥”是“∥且∥”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A3.对于平面和共面的直线,,下列命题是真命题的是()A.若,与平面所成的角相等,则B.若,,则C.若,,则D.若,,则解析:由m⊂α,n∥α可知m与n不相交,又m与n共面,故m∥n.答案:D4.如图,在四面体中,,分别是面,的重心,求证:平面,平面解析:连接AM并延长,交CD于E,连接BN并延长交CD于F,由重心性质可知,E、F重合为一点,且该点为CD的中点E由==得MN∥AB,因此,MN∥平面ABC且MN∥平面ABD.答案:平面ABC、平面ABD5.如图,在四棱锥PABCD中,点E是CD的中,点F是棱PD的中点.试判断直线EF与平面PAC的关系,并说明理由解析:当点E为CD的中点时,EF∥平面PAC, 点E,F分别是CD,PD的中点,∴EF∥PC. PC⊂平面PAC,EF⊄平面PAC,∴EF∥平面PAC.6.如图所示,在直四棱柱ABCDA1B1C1D1中,底面是正方形,E,F,G分别是棱B1B,D1D,DA的中点.求证:平面AD1E∥平面BGF.【证...