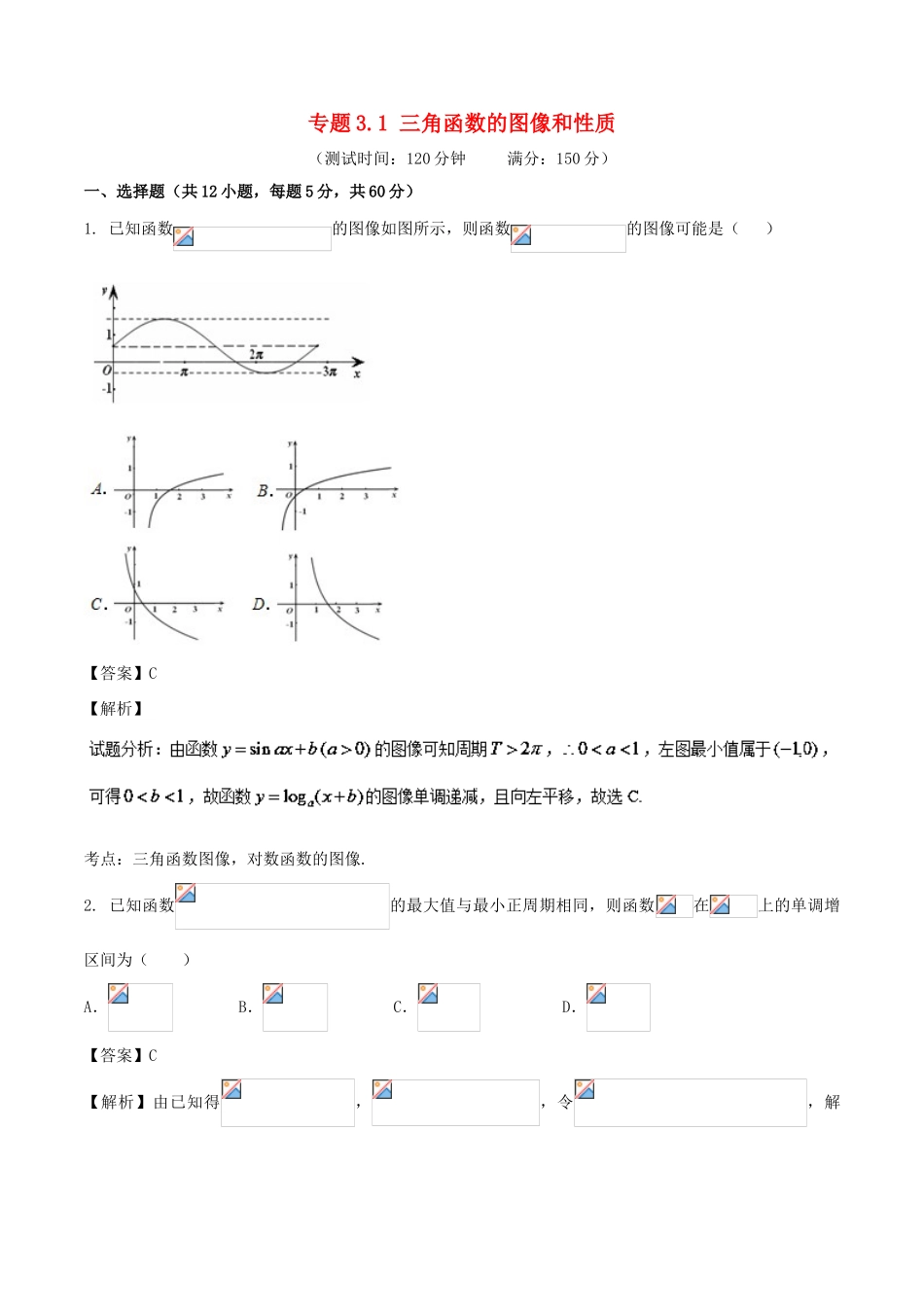
专题3.1三角函数的图像和性质(测试时间:120分钟满分:150分)一、选择题(共12小题,每题5分,共60分)1.已知函数的图像如图所示,则函数的图像可能是()【答案】C【解析】考点:三角函数图像,对数函数的图像.2.已知函数的最大值与最小正周期相同,则函数在上的单调增区间为()A.B.C.D.【答案】C【解析】由已知得,,令,解得,又,所以,所以函数在上的单调递增区间为考点:三角函数的图像和性质3.【2018辽宁省沈阳两校联考】已知函数(为常数,)的图像关于直线对称,则函数的图象()A.关于点对称B.关于点对称C.关于直线对称D.关于直线对称【答案】C【解析】因为函数(为常数,)的图像关于直线对称,所以,可得,,,函数的对称轴方程为,当时,对称轴为,数的图象关于关于直线对称,故选C.4.若函数满足,且函数在上有且只有一个零点,则的最小正周期为()A.B.C.D.【来源】【百强校】2016届湖南永州市高三下学期第三次模拟数学(理)试卷(带解析)【答案】B【解析】考点:1、三角函数图象及其性质;2、函数零点.5.已知函数(其中),其部分图像如下图所示,将的图像纵坐标不变,横坐标变成原来的2倍,再向右平移1个单位得到的图像,则函数的解析式为()A.B.C.D.【答案】B【解析】考点:三角函数的图像及性质.6.对于函数,给出下列四个结论①函数的最小正周期为②函数在上的值域是③函数在上是减函数④函数的图象关于点对称其中正确结论的个数是()A.1个B.2个C.3个D.4个【答案】B【解析】考点:三角恒等变换;三角函数的图象与性质.【方法点晴】本题主要考查了三角恒等变换、三角函数的图象与性质——单调性、对称轴、对称中心、定义域、值域等性质的综合应用,解答中把函数化简为,再根据的取值范围,进而求解函数的性质,着重考查了学生对三角函数的图象与性质的掌握,以及解答问题和分析问题的能力,属于中档试题.7.使在区间至少出现2次最大值,则ω的最小值为()A.B.C.D.【答案】A【解析】要使在区间至少出现2次最大值只需要最小正周期1,故。考点:三角函数的性质8.已知函数在上有两个零点,则的取值范围为()A.B.C.D.【来源】【百强校】2017届湖北襄阳四中高三七月周考二数学(理)试卷(带解析)【答案】B【解析】试题分析:因,故,由于函数在上单调递增;在上单调递减,且,故当时,函数的图象与直线有两个交点,应选B.考点:三角函数的图象与性质.【方法点晴】本题主要考查三角函数的图象与性质,属于中等难题,先有得,由于函数在上单调递增;在上单调递减,且当时,函数的图象与直线有两个交点.此类题型要求考生熟练掌握函数的图像与性质,才能迅速找到解题的突破口.9.【2018河北衡水二调】已知函数(,),其图像与直线相邻两个交点的距离为,若对于任意的恒成立,则的取值范围是()A.B.C.D.∴函数的周期为,故,∴。∴.由题意得“对于任意的恒成立”等价于“对于任意的恒成立”。 ,∴,∴,∴。故结合所给选项可得C正确。选C。点睛:本题难度较大,解题时根据题意得,可将问题转化成“函数对于任意的恒成立”,然后可根据在上的取值范围是的子集去处理,由此通过不等式可得的范围,结合选项得解。10.【2018河南漯河中学二模】设函数的定义域为,且,当时,,则函数在区间上的所有零点的和为()A.4B.3C.2D.1【答案】B函数在区间上的零点的和为:0.函数在时,两个函数的交点关于x=1对称,零点有3个,零点的和为:3.故选:B.点睛:本题考查函数与方程的综合应用,抽象函数以及数形结合思想方法的应用,考查作图能力以及计算能力,函数零点的问题都转化为两个函数图像的交点问题,数形结合的思想是本题要考查的关键.11.先把函数的图象上各点的横坐标变为原来的(纵坐标不变),再把新得到的图象向右平移个单位,得到的图象,当时,函数的值域为()A.B.C.D.【来源】【百强校】2017届广西陆川县中学高三8月月考数学(理)试卷(带解析)【答案】A【解析】考点:三角函数的图象与性质.12.已知函数,给出下列四个说法:①函数的周期为;②若,则;③在区间上单调递增;④的图象关于点中心对称.其中正确说法的个数是()A.3个B.2个C....