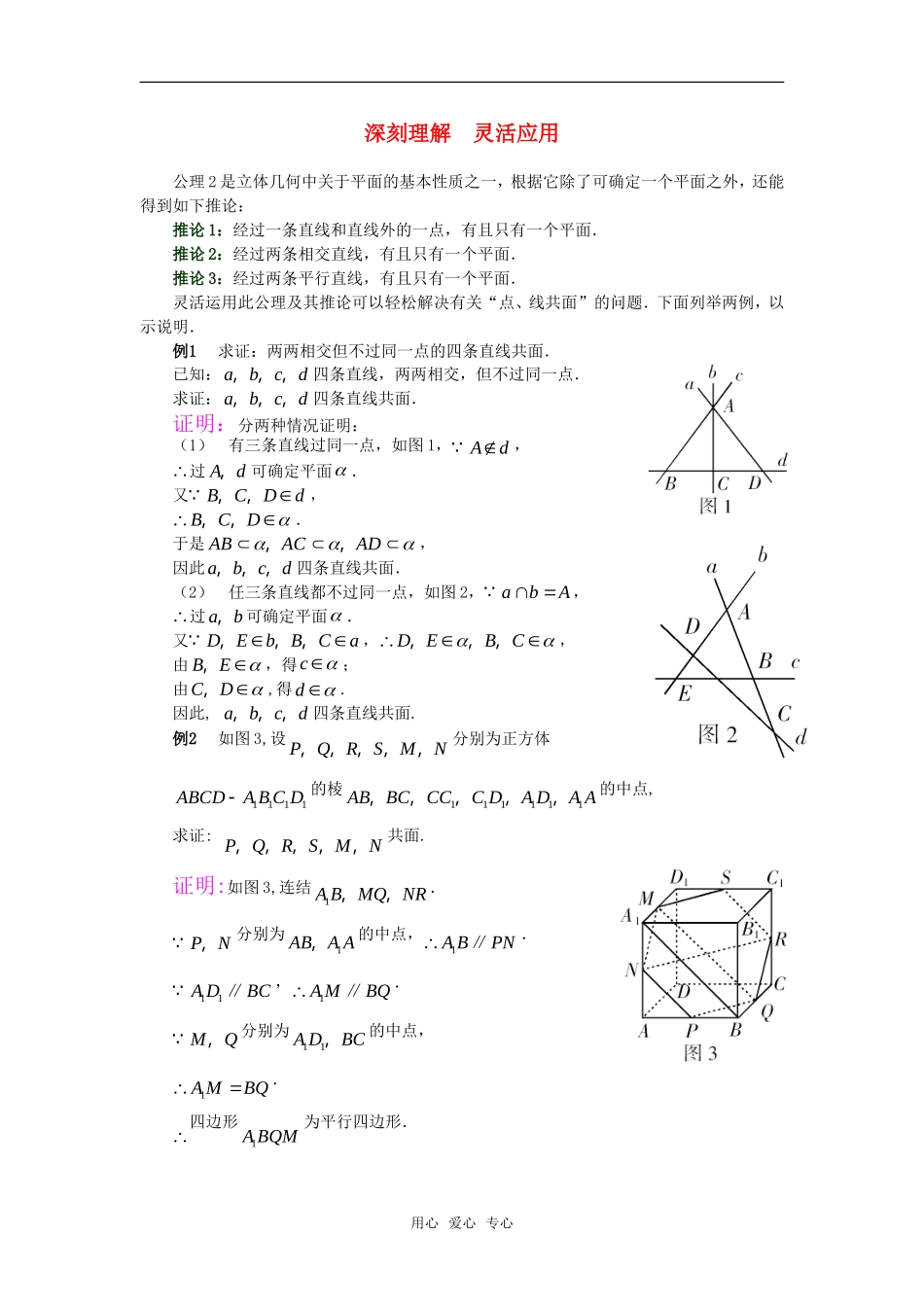
深刻理解灵活应用公理2是立体几何中关于平面的基本性质之一,根据它除了可确定一个平面之外,还能得到如下推论:推论1:经过一条直线和直线外的一点,有且只有一个平面.推论2:经过两条相交直线,有且只有一个平面.推论3:经过两条平行直线,有且只有一个平面.灵活运用此公理及其推论可以轻松解决有关“点、线共面”的问题.下面列举两例,以示说明.例1求证:两两相交但不过同一点的四条直线共面.已知:abcd,,,四条直线,两两相交,但不过同一点.求证:abcd,,,四条直线共面.证明:分两种情况证明:(1)有三条直线过同一点,如图1,Ad,过Ad,可确定平面.又BCDd,,,BCD,,.于是ABACAD,,,因此abcd,,,四条直线共面.(2)任三条直线都不过同一点,如图2,abA,过ab,可确定平面.又DEbBCa,,,,DEBC,,,,由BE,,得c;由CD,,得d.因此,abcd,,,四条直线共面.例2如图3,设PQRSMN,,,,,分别为正方体1111ABCDABCD的棱111111ABBCCCCDADAA,,,,,的中点,求证:PQRSMN,,,,,共面.证明:如图3,连结1ABMQNR,,.PN,分别为1ABAA,的中点,1ABPN∥.11ADBC∥,1AMBQ∥.MQ,分别为11ADBC,的中点,1AMBQ.四边形1ABQM为平行四边形.用心爱心专心1ABMQ∥.PNMQ∥.因此,直线PNMQ,可确定一个平面.同理,由PQNR∥可知,直线PQNR,确定一个平面.过两条相交直线PNPQ,有且只有一个平面,与重合,即R.同理可证S.因此,PQRSMN,,,,,共面.由以上两例可以看出,证明空间的点、线共面问题,通常采用以下两种方法:①根据已知条件先确定一个平面,再证明其他点或直线也在这个平面内;②分别过某些点或直线作两个平面,再证明这两个平面重合.用心爱心专心