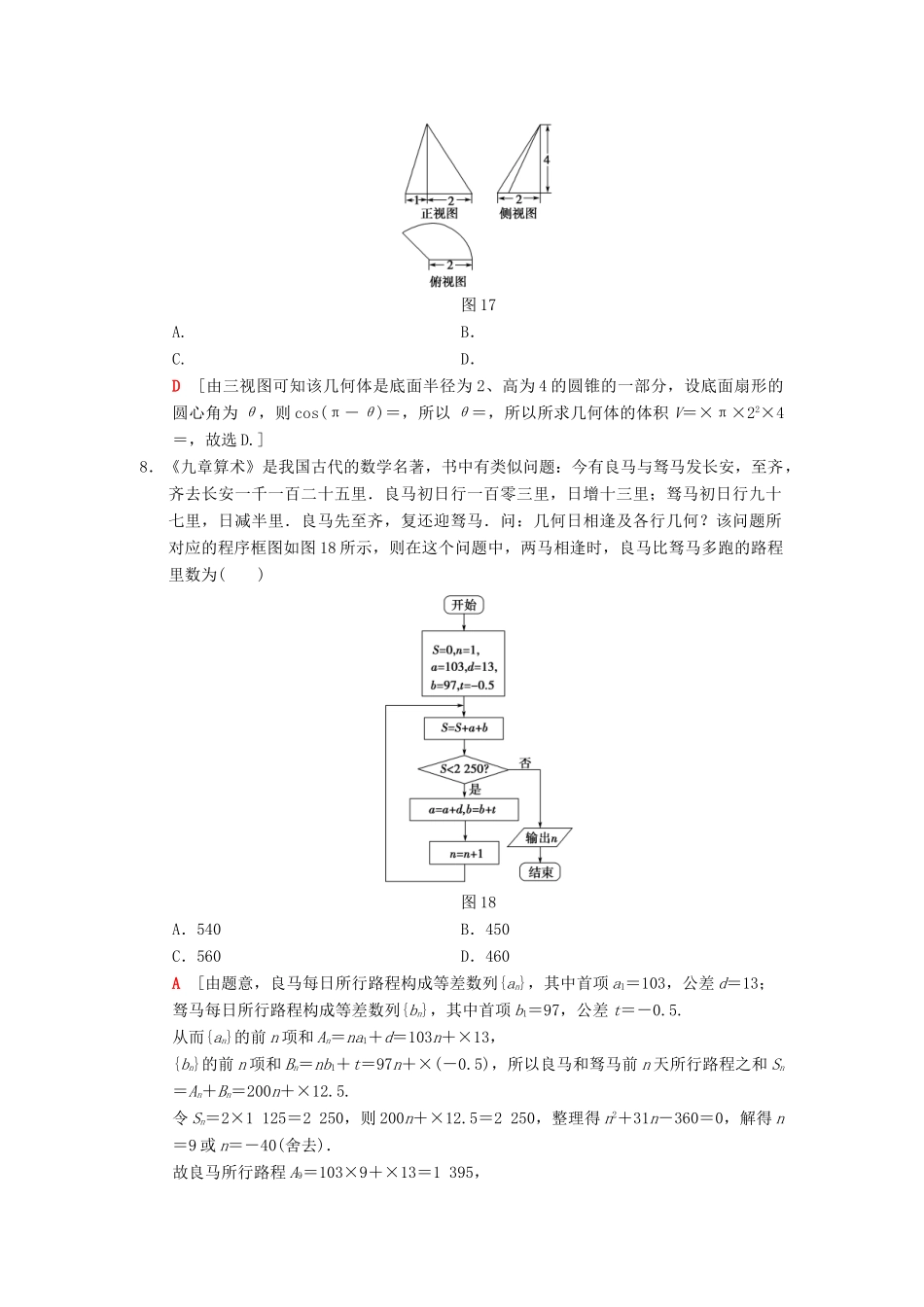
小题提速练(七)“12选择+4填空”80分练(时间:45分钟分值:80分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合A={x|0≤x≤5},B={x∈N*|x-1≤2},则A∩B=()A.{x|1≤x≤3}B.{x|0≤x≤3}C.{0,1,2,3}D.{1,2,3}D[因为B={x∈N*|x≤3}={1,2,3},所以A∩B={1,2,3},故选D.]2.若z是复数,z=,则z·=()A.B.C.1D.D[因为z===--i,所以=-+i,所以z·==,故选D.]3.已知等差数列{an}的公差为5,前n项和为Sn,且a1,a2,a5成等比数列,则S6=()A.80B.85C.90D.95C[由题意,得(a1+5)2=a1(a1+4×5),解得a1=,所以S6=6×+×5=90,故选C.]4.(2017·广东梅州一模)设椭圆+=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为,则此椭圆的方程为()【导学号:07804220】A.+=1B.+=1C.+=1D.+=1B[y2=8x的焦点坐标为(2,0),即c=2,所以椭圆的焦点在x轴上,排除A,C,又e==,所以a=4,故排除D.故选B.]5.若a=,b=,c=log10,则a,b,c的大小关系为()A.a>b>cB.a>c>bC.c>b>aD.b>a>cD[0<<0=1,即0<a<1,=5>50=1,即b>1,又c<0,所以b>a>c,故选D.]6.已知(1+ax)(1+x)5的展开式中x2的系数为5,则a=()A.-4B.-3C.-2D.-1D[(1+x)5中含有x与x2的项为T2=Cx=5x,T3=Cx2=10x2,∴x2的系数为10+5a=5,∴a=-1,故选D.]7.某几何体的三视图如图17所示,其中俯视图为扇形,则该几何体的体积为()图17A.B.C.D.D[由三视图可知该几何体是底面半径为2、高为4的圆锥的一部分,设底面扇形的圆心角为θ,则cos(π-θ)=,所以θ=,所以所求几何体的体积V=×π×22×4=,故选D.]8.《九章算术》是我国古代的数学名著,书中有类似问题:今有良马与驽马发长安,至齐,齐去长安一千一百二十五里.良马初日行一百零三里,日增十三里;驽马初日行九十七里,日减半里.良马先至齐,复还迎驽马.问:几何日相逢及各行几何?该问题所对应的程序框图如图18所示,则在这个问题中,两马相逢时,良马比驽马多跑的路程里数为()图18A.540B.450C.560D.460A[由题意,良马每日所行路程构成等差数列{an},其中首项a1=103,公差d=13;驽马每日所行路程构成等差数列{bn},其中首项b1=97,公差t=-0.5.从而{an}的前n项和An=na1+d=103n+×13,{bn}的前n项和Bn=nb1+t=97n+×(-0.5),所以良马和驽马前n天所行路程之和Sn=An+Bn=200n+×12.5.令Sn=2×1125=2250,则200n+×12.5=2250,整理得n2+31n-360=0,解得n=9或n=-40(舍去).故良马所行路程A9=103×9+×13=1395,驽马所行路程B9=97×9+×(-0.5)=855.良马比驽马多行路程里数为1395-855=540.故选A.]9.已知双曲线-x2=1的两条渐近线分别与抛物线y2=2px(p>0)的准线交于A,B两点.O为坐标原点.若△OAB的面积为1,则p的值为()A.1B.C.2D.4B[双曲线的两条渐近线方程为y=±2x,抛物线的准线方程为x=-,故A,B两点的坐标为,|AB|=2p,所以S△OAB=·2p·==1,解得p=,故选B.]10.如图19所示,周长为1的圆的圆心C在y轴上,点A(0,1)为圆C与y轴的上交点,一动点M从A开始逆时针绕圆运动一周,记=s,直线AM与x轴交于点N(t,0),则函数t=f(s)的图象大致为()图19D[当s由0→时,t从-∞→0,且t=f(s)在上单调递增;当s由→1时,t从0→+∞,且t=f(s)在上也单调递增.∴排除A,B,C,故选D.]11.在三棱锥SABC中,SB⊥BC,SA⊥AC,SB=BC,SA=AC,AB=SC,且三棱锥SABC的体积为,则该三棱锥的外接球的半径为()【导学号:07804221】A.1B.2C.3D.4C[如图,取SC的中点O,连接OB,OA,因为SB⊥BC,SA⊥AC,SB=BC,SA=AC,所以OB⊥SC,OA⊥SC,OB=SC,OA=SC,所以SC⊥平面OAB,O为外接球的球心,SC为球O的直径,设球O的半径为R,则AB=SC=R,所以△AOB为正三角形,所以∠BOA=60°,所以VSABC=VSOAB+VCOAB=2×R2sin60°××R=,解得R=3,故选C.]12.已知函数f(x)=(n∈N),若数列{am}满足am=f(m)(m∈N*),数列{am}的前m项和为Sm,则S105-S96=()A.909B.910C.9...