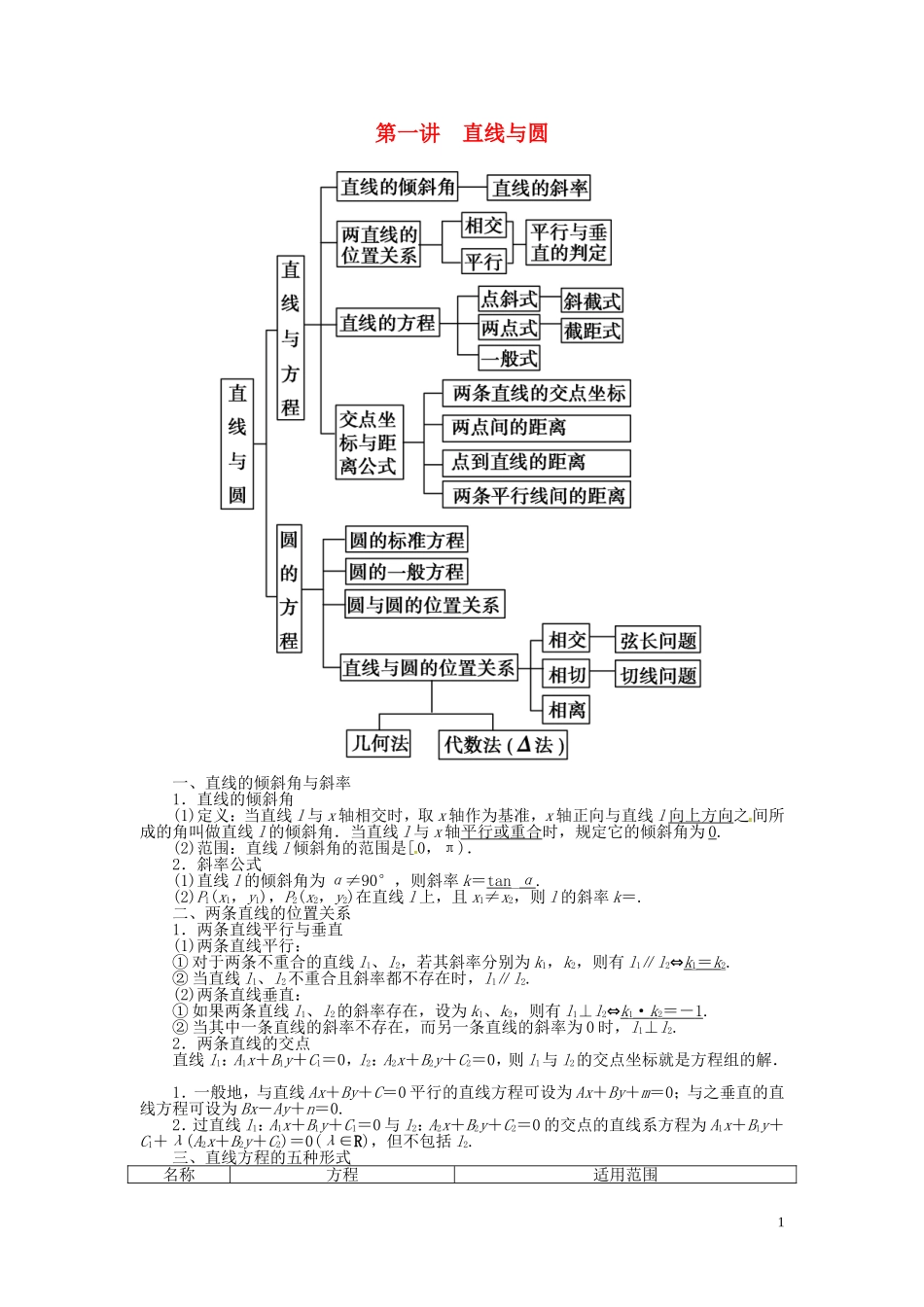
第一讲直线与圆一、直线的倾斜角与斜率1.直线的倾斜角(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为0.(2)范围:直线l倾斜角的范围是[0,π).2.斜率公式(1)直线l的倾斜角为α≠90°,则斜率k=tan_α.(2)P1(x1,y1),P2(x2,y2)在直线l上,且x1≠x2,则l的斜率k=.二、两条直线的位置关系1.两条直线平行与垂直(1)两条直线平行:①对于两条不重合的直线l1、l2,若其斜率分别为k1,k2,则有l1∥l2⇔k1=k2.②当直线l1、l2不重合且斜率都不存在时,l1∥l2.(2)两条直线垂直:①如果两条直线l1、l2的斜率存在,设为k1、k2,则有l1⊥l2⇔k1·k2=-1.②当其中一条直线的斜率不存在,而另一条直线的斜率为0时,l1⊥l2.2.两条直线的交点直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则l1与l2的交点坐标就是方程组的解.1.一般地,与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0;与之垂直的直线方程可设为Bx-Ay+n=0.2.过直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的交点的直线系方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ∈R),但不包括l2.三、直线方程的五种形式名称方程适用范围1点斜式y-y0=k(x-x0)不含直线x=x0斜截式y=kx+b不含垂直于x轴的直线两点式=不含直线x=x1(x1≠x2)和直线y=y1(y1≠y2)截距式+=1不含垂直于坐标轴和过原点的直线一般式Ax+By+C=0,A2+B2≠0平面内所有直线都适用四、几种距离公式1.两点P1(x1,y1),P2(x2,y2)之间的距离|P1P2|=.2.点P0(x0,y0)到直线l:Ax+By+C=0的距离d=.3.两条平行线Ax+By+C1=0与Ax+By+C2=0(其中C1≠C2)间的距离d=.点到直线与两平行线间的距离的使用条件:(1)求点到直线的距离时,应先化直线方程为一般式.(2)求两平行线之间的距离时,应先将方程化为一般式且x,y的系数对应相等.五、圆的定义及方程定义平面内到定点的距离等于定长的点集合限定条件标准方程(x-a)2+(y-b)2=r2圆心:(a,b),半径:rr>0一般方程x2+y2+Dx+Ey+F=0圆心:,半径:D2+E2-4F>0确定圆的方程时,常用到的三个性质(1)圆心在过切点且与切线垂直的直线上(2)圆心在任一弦的中垂线上(3)两圆内切或外切时,切点与两圆圆心三点共线.1、点M(x0,y0)与圆(x-a)2+(y-b)2=r2的位置关系(1).若M(x0,y0)在圆外,则(x0-a)2+(y0-b)2>r2.(2).若M(x0,y0)在圆上,则(x0-a)2+(y0-b)2=r2.(3).若M(x0,y0)在圆内,则(x0-a)2+(y0-b)2<r2.从位置看d,r的关系判定点与圆的位置关系还可利用点到圆心的距离d与r的关系:d>r⇔点在圆外;d=r⇔点在圆上;d<r⇔点在圆内.2、圆与圆的位置关系设圆O1:(x-a1)2+(y-b1)2=r(r1>0),圆O2:(x-a2)2+(y-b2)2=r(r2>0).方法位置关系几何法:圆心距d与r1,r2的关系代数法:联立两圆方程组成方程组的解的情况相离d>r1+r2无解外切d=r1+r2一组实数解相交|r1-r2|<d<r1+r2两组不同的实数解内切d=|r1-r2|(r1≠r2)一组实数解内含0≤d<|r1-r2|(r1≠r2)无解常用结论(1)两圆的位置关系与公切线的条数:①内含时:0条;②内切:1条;③相交:2条;④外切:3条;⑤外离:4条.(2)当两圆相交时,两圆方程(x2,y2项系数相同)相减便可得公共弦所在直线的方程.3、判断直线与圆的位置关系常用的两种方法(1).几何法:利用圆心到直线的距离d和圆半径r的大小关系:d<r⇔相交;d=r⇔相切;d>r⇔相离.(2).代数法:――→圆的切线方程常用结论(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.(3)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为x0x+y0y=r2.基础自测1.直线x-y+a=0的倾斜角为()A.30°B.60°C.150°D.120°【解析】k=tanα=,且0°≤α<180°,∴α=60°.【答案】B2.(2009·安徽高考)直线l过点(-1,2)且与直线2x-3y+4=0垂直,则l的方程是()2A.3x+2y-1=0B.3x+2y+7=0C.2x...